1.5: Seasons
- Page ID
- 2233
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)What causes seasons? The distance between the Earth and the Sun does not account for the seasons. Look at page xii in Goodes World Atlas. First, you will note that the earth’s orbit is indeed not quite circular. The distance between the sun and the earth on the winter solstice (December 22) is 91.5 million miles, while the distance between the sun and the earth on the summer solstice is a whopping 94.5 million miles. So the earth is actually closer to the sun in December than it is in June! Click on the image thumbnail below to see a full-size image of Spreading Sunlight Over the Spherical Earth.
Figure 1.6.1 Earth - Sun Relationships and Solar Energy
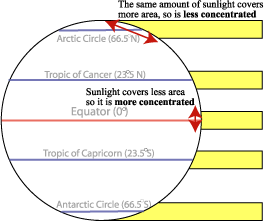
The earth is tilted 23.5 degrees off of vertical, and this tilt accounts for the seasons. Insolation is distributed over the (nearly) spherical earth. The sunlight is most concentrated at the point where the ray of the sun is perpendicular to the tangent of the earth. As the angle between the sun’s rays and the tangent becomes smaller, the effect is that the same amount of sun energy is spread over a larger area. Or, each area gets less energy. The graphic below is another way to visualize this concept:
Figure 1.6.2 Solar energy spread over earth's surface
The seasons are caused not by distance from the sun, but by the effect of the uneven distribution of sunlight on the tilted earth. The earth rotates around the sun on a flat plane. This is called the plane of the ecliptic. The earth is tilted 23.5 degrees off of this plane. The tilt does not change, a concept called axial parallelism. In other words, the axis of the earth is parallel to itself throughout the orbit.
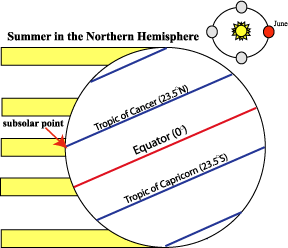
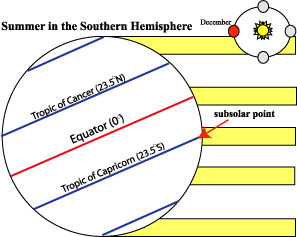
You can see in the diagram below (Earth Sun relationships and Incoming Solar Energy) that at the December solstice, the majority of the incoming solar energy is in the Southern Hemisphere, and in June, the majority of the incoming solar energy is in the northern hemisphere. That is because on the December solstice, the sun’s rays are perpendicular to the earth at 23.5 degrees South. This is the subsolar point, or the point of maximum insolation. On the June solstice, the subsolar point is at 23.5 degrees north (see the graphic below). The subsolar points at the solstices define the Tropics. The Tropic of Cancer is 23.5 degrees North, and the Tropic of Capricorn is 23.5 degrees South. At this point it is worth pointing out that while the northern hemisphere experiences summer in June, the southern hemisphere experiences summer in December. Another way to think about it is that the southern hemisphere is ‘in reverse’ of our seasons in the northern hemisphere.
Figure 1.6.3: (left) Summer in Northern Hemisphere. (rigth) Summer in Southern Hemisphere
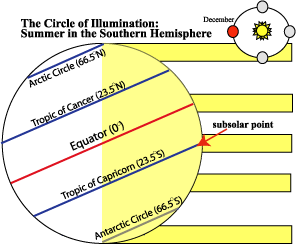
The next piece of the puzzle is the Circle of illumination. At any time, half of the earth is illuminated by our sun. If the earth had no tilt, this would mean that we could have 12 hours of daylight and 12 hours of darkness everywhere on earth all the time, and as there would be no shift in the subsolar point, we would not have seasons. As I am sure you are aware, this is not the case! If you have every traveled anyplace very far north in the summertime, for example, you may have noted the very long days. I vividly recall sitting in a garden pub while I was in graduate school in England (at about 53 degrees N) and enjoying the sunset at 10PM! The circle of illumination defines the Arctic Circle and the Antarctic circle (see below). How long are the days in the Arctic Circle in June? How long are the days in the Antarctic Circle in June? Why?
Figure 1.6.5: (left) The circle of Illumination Northern Hemisphere. (right) The circle of Illumination Southern Hemisphere
The equinoxes occur in March and September. I like to think of them as 'equal equinoxes' -- in other words, at the equinox the subsolar point is at the equator and the circle of illumination is distributed equally over the earth. In the Earth Sun Relationships diagram above you can see for yourself that the insolation is pretty much equally distributed over the northern and southern hemispheres. Visualize what the circle of illumination looks like at the equinoxes. How long are the days at various latitudes at the equinoxes?
To review key points:
- The Earth's tilted axis (23.5 degrees) causes some parts of the Earth to receive direct sunlight while other parts are receiving indirect sunlight.
- Seasons occur due to the tilt of the Earth's axis and the orbit of the Earth around the Sun.
- The seasons of the Northern and Southern Hemispheres are reversed: when the Northern Hemisphere is experiencing winter, the Southern Hemisphere is experiencing summer.
- The vernal equinox: the first day of spring in the Northern Hemisphere (March 21), when the Sun is perpendicular to the equator.
- The summer solstice: first day of summer in the Northern Hemisphere (June 21), when the Sun is perpendicular to the tropic of Cancer.
- The autumnal equinox: first day of autumn in the Northern Hemisphere (September 22), when the Sun is perpendicular to the equator.
- The winter solstice: first day of winter in the Northern Hemisphere (December 21), when the Sun is perpendicular to the Tropic of Capricorn.
- Key terms: plane of the ecliptic, axial parallelism, circle of illumination, subsolar point.