4.4: Plates Moving on a Plane
- Page ID
- 3513
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Relating Plate Motion to Plate Boundaries
Let's start by considering the motion of two rectangular plates: plate A and plate B. Let's hold plate B fixed in space so it is not moving. If plate A moves away from plate B space is created between the two plates. On the surface of the earth, this space is filled in through melting of the mantle beneath the plate boundary and emplacement or eruption of the magma to form oceanic crust. This plate boundary is referred to as divergent boundary or a spreading center. If plate A moves toward plate B, it either needs to compress or slide above or beneath plate B. On the surface of the Earth, this motion is accommodated either through shortening of plates A and B in a collision (case 1) or plate A needs to sink into the mantle below plate B (or vice versa), a process known as subduction (case 2). This type of plate boundary is referred to as a convergent boundary or as collision zone (case 1) or subduction zone (case 2). If plate A slides past plate B parallel to the plate boundary, then no plate is created or destroyed at the plate boundary. This plate boundary is referred to as transform boundary and exhibits strike-slip motion (meaning motion parallel to the strike of the boundary.
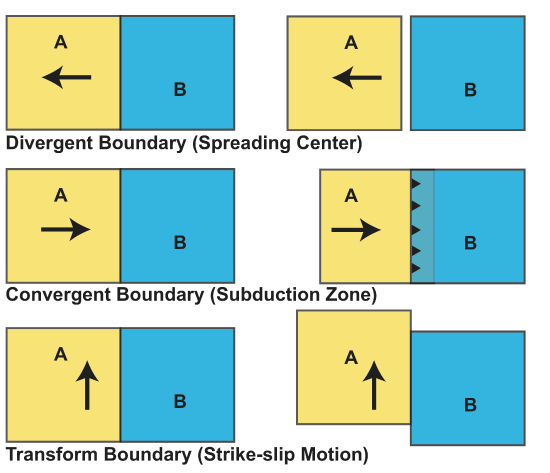
Now consider a slightly more interesting geometry in which plate A has a triangle shape. Depending on the direction that plate A moves relative to plate B and relative to the plate boundaries, the motion across the plate boundaries changes, and thus the type designation for each plate boundary changes. For example, if plate A moves parallel to the side 2 and toward plate B, then the boundary at side 2 is a transform and the boundary at side 3 is a convergent boundary. However, with a small change in the direction of plate A to the north, side 2 becomes a spreading center. In this case because the motion of plate A is not perpendicular to or parallel to the plate boundary, we say that the motion is oblique. There is oblique divergence at side 2 and oblique convergence at side 1. Such oblique motions are often manifest in different geometry of faults than at non-oblique boundaries. These faults work together to partition the deformation into parallel and perpendicular components.

From these two simple examples, we can see that plate boundary types, in a plate tectonic sense, are defined by the relative velocity of the plates across the boundary. As the forces driving plate motion change, the relative velocity can change. If the change in velocity is large enough it can lead to a change in the type of plate boundary. As an example, this type of plate boundary change is occurring across the Macquarie Ridge south of New Zealand. This boundary was a spreading center where the Pacific plate was moving away from the Indian Plate. However, in recent times, the plate motions have change such that the two plates are converging across the same plate boundary turning it into an incipient subduction zone.
Let's do an example together demonstrating how plates move.
Plate Motion on a Plane
From the figure below, we can see that A is fixed, and the trench is fixed to A. The ridge moves with B and leaves a trail behind. Let's say we started out with the below configuration at 10 MA. What does it look like now?
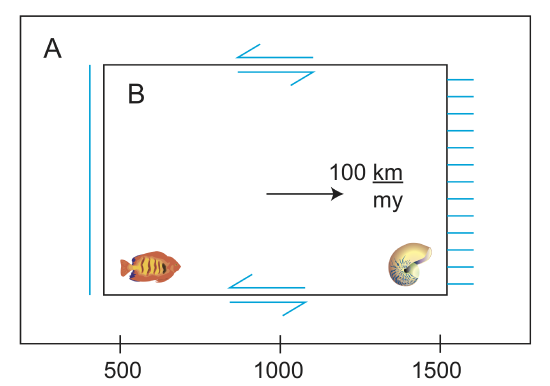
Solution
10 my⇒10 my\(\frac{100 km}{my}\)=1000 km
Which plate moves 1000 km? Plate B. But, plate B is also growing at \(\frac{1}{2}V\), as is plate A. So how do we account for that to determine the total plate motion?
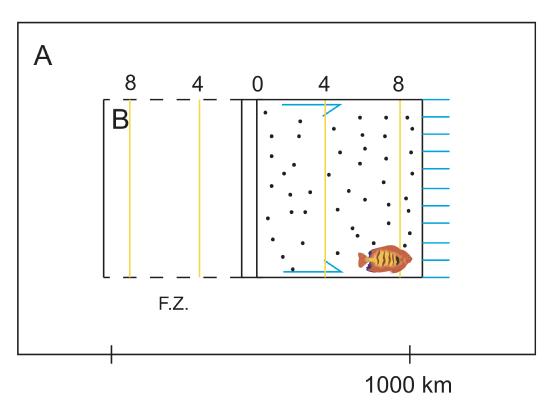
1. Fish moves 1000 km
2. Ridge moves half as far
3. Stipple in plate B
4. What are the trails of the Transform Fault?⇒F.Z.
5. Ridge is at 0. Old ridge is at 10 MA, ridge was moving ⇒ at rate of 50 \(\frac{km}{my}\)
At 8 Ma, 2my (50\(\frac{km}{my}\))=100 km
At 4 Ma, 4 my (50\(\frac{km}{my}\))=200 km


