3.7: Gravitational Potential, Mass Anomalies and the Geoid
- Page ID
- 3521
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Determining the layered structure of a planet requires knowing the gravitational field around a planet and in particular the elliptical shape of the gravity field. Recall from the previous section, that the oblate (ellipsoidal) shape of the planet is a direct result of the viscous flow of a spinning planet. However, the gravity field can also provide information about density anomalies inside the planet and the viscosity layering in the convecting (mantle) part of the planet. Therefore, here we spend more time describing the relationship between the gravity (acceleration) we are familiar with from introductory physics, and the gravitational potential field.
The gravitational potential, \(U\) is defined as,
\[U = -\frac{Gm}{r}\]
and gravity, \(g\) the acceleration caused be the gravitational potential is the gradient of the potential field
\[g = -\triangledown U = -\left(\frac{dU}{dx} + \frac{dU}{dy} + \frac{dU}{dz} \right)\]
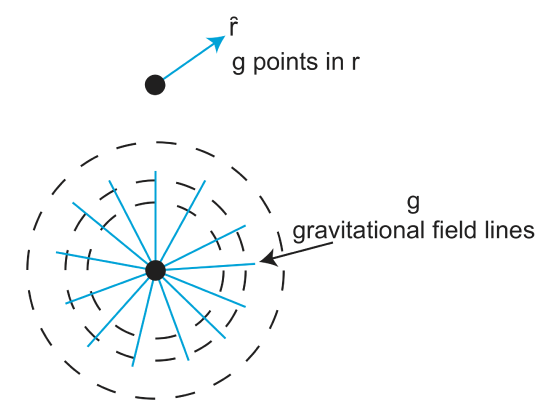
While we don't usually think of gravity as a field quantity, we are probably familiar with the concept of a field from magnetism. Consider a bar magnet, with positive (north) end and negative (south) end. We usually illustrate the magnetic field as lines that come out one end of the magnet and go back in at the other side of the magnet. This magnetic field is create by two magnetic poles (positive and negative). The strength of the magnetic field is strongest near the poles and decays (and switches sign) along these field lines.
Similarly, we can think of gravity as originating at a single "pole", a point mass, with gravity field lines that point radially outward. The strength of gravitational field also decays along these field line. The gravitational potential around a point mass is represented by spherical surfaces centered on the point mass. The magnitude of the gravitational potential, \(U(r)\) is a constant on each of these surfaces: therefore, these surfaces are referred to as equipotential surfaces. Spherical surfaces at greater distances have lower values because (\(U\) decreases proportional to \(1/r\)).
Gravity, \(g\), or the gravitational acceleration at any point, is the gradient of this three-dimensional potential field, and has both a magnitude and a direction. For a point mass or a perfect sphere, \(g\), points radially outward (it is perpendicular to the spherical equipotential surface) and its magnitude is the same everywhere on one of the equipotential surfaces (for a perfect sphere, but not other shapes, as we will see). When we say that gravity is 9.81 m/s\(^2\), we are actually stating the average value of \(g\) on the equipotential surface that is close to concentric with the surface (sea-level) of the Earth. If we move to an equipotential surface further from the Earth, the gradient will be lower and therefore the value of \(g\) decreases. Note that, for a point mass or a perfect sphere
\[ g = - \triangledown U = \frac{dU}{dr} = \frac{d}{dr}\left(-\frac{Gm}{r}\right) = \frac{Gm}{r^2} \]
which gives the more familiar equation for the gravitational acceleration from a point mass, \(g = \frac{Gm}{r^2}\).
Reference Equipotential Gravity Surface, \(U_{ref}\)
Note, that the because the Earth's shape is ellipsoidal (as discussed in the previous section), the gravitational potential surfaces will also be ellipsoidal: there first-order shape follows the oblate shape of the planet. This is what allowed us to use measurements of the gravitational potential to determine the \(J_2\) term needed to find the moment of inertia factor.
It is useful to introduce the idea of a reference gravitational potential surface, \(U_{ref}\) because then we can measure perturbations to a planet's gravitational field and related these to mass anomalies inside.
\[U_{ref} = - \frac{GM}{r}+ J_2\left(\frac{GMa^2}{2r^3}\right)[3\sin^2\phi-1]-\frac{1}{2}\omega^2r^2\cos^2\phi\]
where the first term is due to the underlying spherical shape, the second term accounts for the equatorial bulge (of the viscous "hyrostatic" solid mantle), and the third term is due to the actual spin of the planet. This reference equipotential surface is either predicted (given the known structure of the planet) or determined by fitting the observed field, which is how we get the observed value of \(J_2\). Note that this is the same equipotential surface that is used to determine the hydrostatic flattening term, \(f_{hyd}\). The term hydrostatic refers to the assumption of a viscously deformable planet.
Mass Anomalies On and In a Planet
Planets like Earth, which has mantle convection, have regions where the rock is either more dense or less dense than the average layered structure. For example, where cold tectonic plates sink back into the mantle, this cold rock is denser than the surrounding. Where hot plumes rise from the core mantle boundary, this rock is less dense (more buoyant) than the surrounding rock. These regions of higher or lower density are termed mass anomalies.
How does the shape of the gravitational potential and the direction of the gravity field lines change if the planet is not a homogeneous or concentrically layered planet?
To answer this question, there are two key points to remember:
- The gravity of the planet can be represented a the sum of the gravity for point mass distributed throughout the planet. This means that if I add mass locally, I can imagine adding a spherical gravitational potential field from that mass to the overall gravitational potential for the whole planet.
- For a given equipotential surface the magnitude of gravity on the surface is a constant and the magnitude is directly proportional to the mass.
Consider the sketch below. This fictitious planet has a giant (not to scale) topographic mass anomaly on one side. The gravitational field from this mass is added to the gravitational field for the rest of the planet. Therefore, near this mass the equipotential surfaces are shifted outward away from the extra mass.
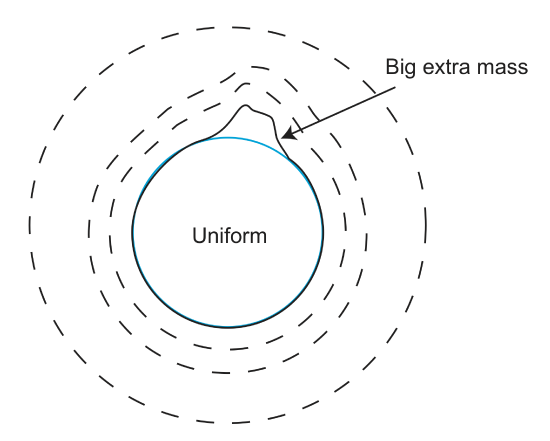
Zooming in on the regions of the planet with the extra topographic mass, we can also consider how the change in the shape of the equipotential surface, from that of a perfect sphere, changes the orientation of the gravity field lines. Remember that the gravity always points perpendicular to the gradient of the potential field. This direction is always mostly radial on the planet, but locally, the direction can be tilted away from the radial direction due to the extra (or missing) mass.
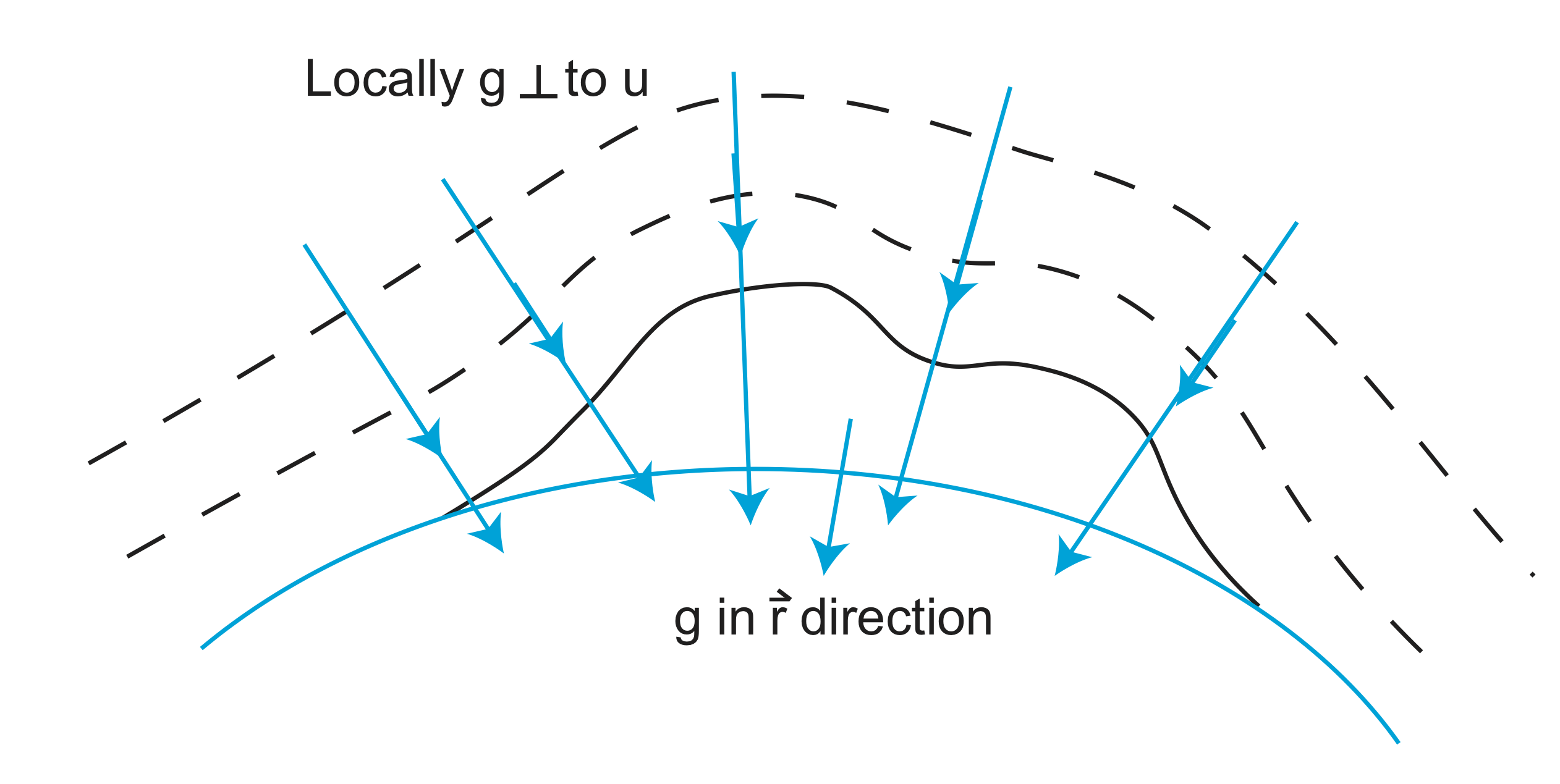
While it may be easier to visualize the mass anomaly from a huge mountain on the surface of a planet, it turns out the biggest undulations of the gravity field come from mass anomalies inside the Earth. This is because most of the mass anomalies due to topography are balanced (compensated) by a mass anomaly of lower density crust immediately underneath (see section on isostasy).
The sketch (meant to be purely schematic) below shows two mass anomalies in an otherwise homogeneous planet. The equipotential surface moves outward above the region with more mass (higher density) and it more inward in the region with less mass (lower density).
Now consider how gravity \(g\) changes due to the mass anomalies. How does the gradient in the potential surface change near these anomalies? Imagine that the blue (solid) line is the surface of the planet. As you walk north along this line starting at the equator you measure a constant value of gravity \(g_o\) until you reach the region affect by the extra mass. As you keep walking north, the magnitude of the gravity increases to a peak and then decreases again on the other side. The value of \(g\) changes because you are crossing over equipotential surfaces that are at smaller distances (r) from the extra mass and therefore have larger magnitudes of both \(U\) and the gradient of the \(U\).
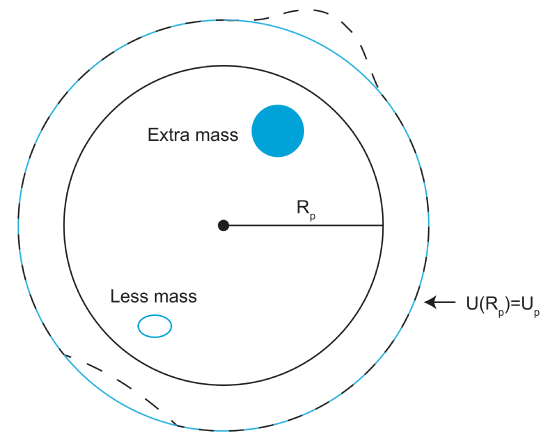
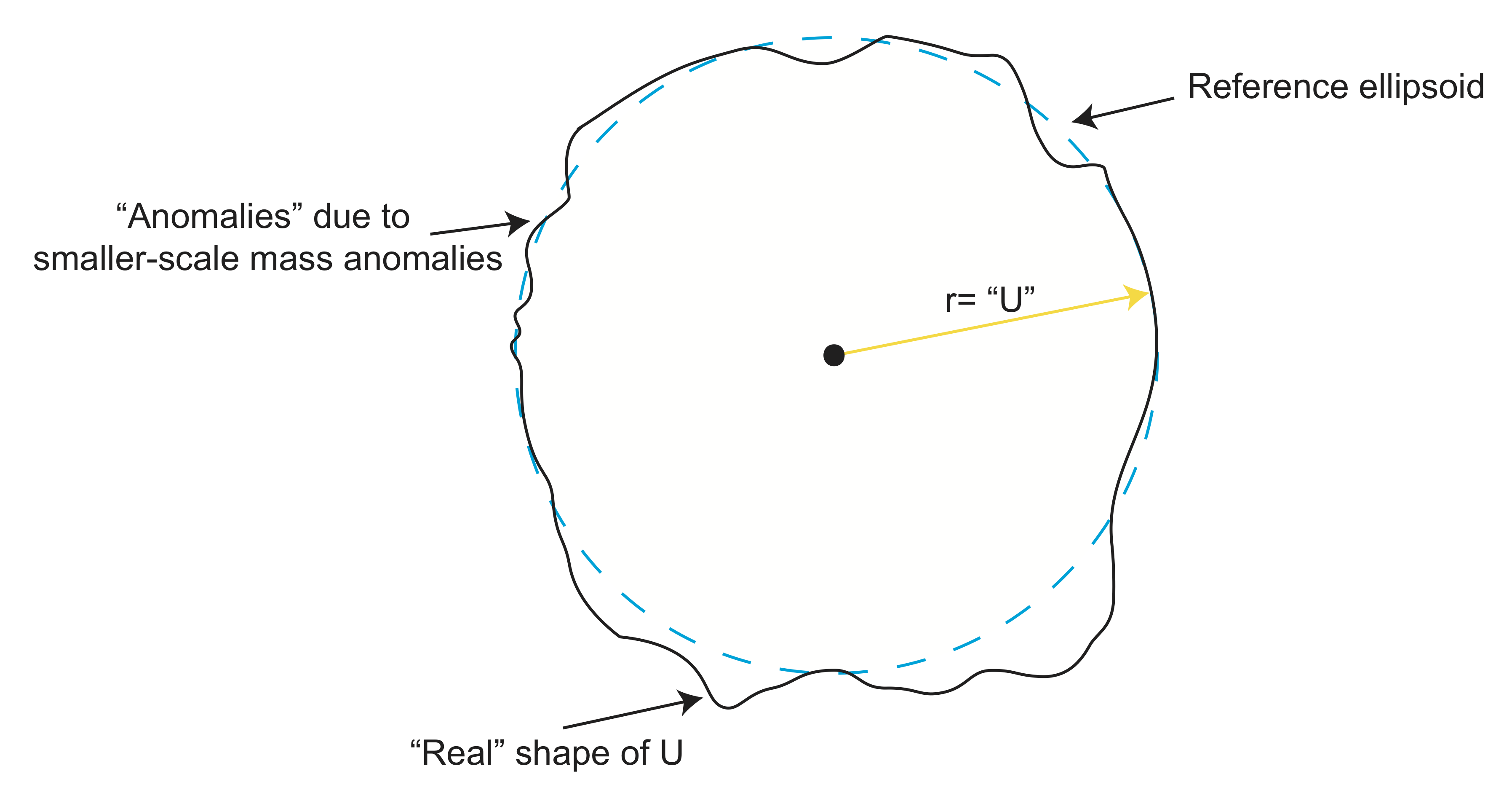
Height of the Geoid or "The Geoid"
Because the undulations in the gravitational equipotential surface are related to mass anomalies in the earth, it is useful to find a way of just representing the undulations rather than always considering the full potential field. The sketch below has to surfaces. The blue dashed line represents the reference equipotential surface discussed above, which accounts all of the signal related the layered structure of the earth. The solid black line represents the observed shape of the equipotential surface that is closest to sea-level: this surface is called the geoid. The height of the geoid above or below the reference equipotential surface,
\[ N = U_{obs} - U_{ref} \]
The height of the geoid is measured in meters: it is the radial distance between the two surfaces at every point. Note that \(N\) is often referred to as the geoid height and also (mistakenly) sometimes referred to as "the geoid" (a confusing shorthand jargon that one gets use to). The geoid height is positive above extra mass and negative above regions with less mass. However, interpreting these undulations is not always straightforward because there can be mass anomalies at multiple depths and sinking or rising mass anomalies can create other mass anomalies at the core-mantle boundary and the Earth's surface due to viscous flow that couples to these boundaries.
Flow Induced Mass Anomalies
[ THIS SECTION NEEDS A NEW FIGURE THAT SHOWS HOW THE SURFACES ABOVE AND BELOW AND DRAGGED/PUSHED DOWNWARD AND CREATE MASS ANOMALIES]
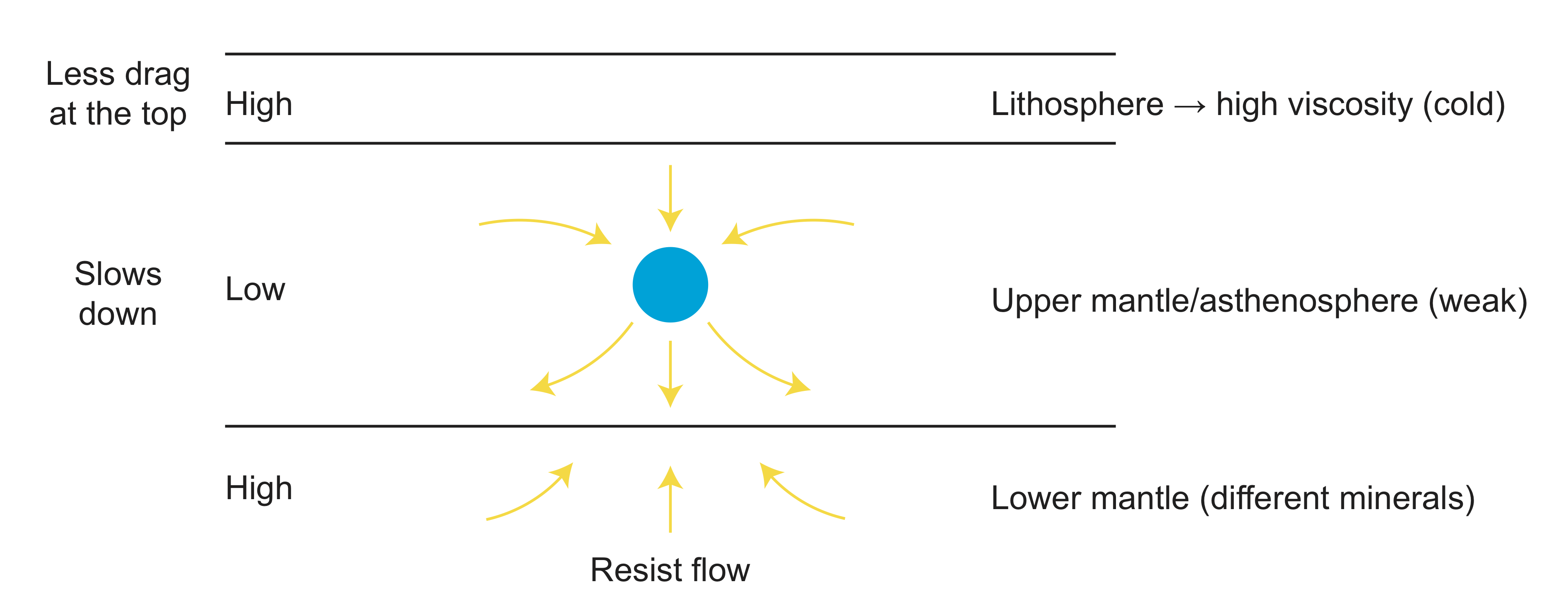
In earth, there are viscous layers as seen below.
- dragging down of the top layer creates a region of less mass because air or water fill in where the lithosphere pulled down.
- below the sinking mass the viscous flow pushes down on the core mantle boundary also creating a region of less mass because less dense mantle material fills in where the denser core material pushed downward.
- the amount the top surface or core-mantle-boundary are deflected depends on viscosity structure of the mantle. In the Earth, the lower mantle has a higher viscosity than the upper mantle. This means that the stress pushing down on the core-mantle boundary will be bigger than the stress pulling down at the surface. So, the mass anomaly at the core-mantle boundary will have a bigger volume than the one at the surface.
The total change to the gravity signal at the surface is due to the original sinking mass anomaly and the flow-induced mass anomalies. The amount each mass anomaly contributes depends on its distance from the surface. In some cases the flow induced mass anomaly at the surface can lead to negative geoid height above a higher density sinking mass because the missing mass at the surface is closer to the surface so it has a bigger effect on the gravity at the surface.
Modeling of the viscous flow and comparison to the observations is one of the primary ways we know the layered viscosity structure inside the mantle.
Spherical Harmonic Representation of the Geoid
The observed gravitational potential field and the geoid height are usually represented in terms of spherical harmonics. Spherical harmonics are like sines and cosines of varying wavelengths, but they depend on (\(\theta,\phi\)) lat/lon. For the purposes of this explanation, let's consider the geoid height, which is just the distance above or below the reference. The figure below shows what the spherical harmonic functions look like on a sphere. Let's consider light regions as being positive geoid height and dark regions as being negative geoid height. Each of the spheres represents one function in the series of spherical harmonics that can be added together to represent the observed geoid height. The first sphere (all white) gives that average value on the sphere. When adding each of the higher order functions, the magnitude of a constant factor in front of each term determines how much of that term is added to the sum. The more functions we include in the summation (higher order) the more detailed (short wavelength) we include in our approximation. Expressing an observation in terms of a sum of spherical harmonic functions is also referred to as a spherical harmonic expansion.
As and example, the expansion of the gravitational potential in terms of spherical harmonics is given by,
\[U=\frac{Gm}{r}\left(1-\sum_{\ell=1}^{\infty}J_2\ell \left[\dfrac{a}{r}\right]^{2\ell}P_{2\ell}(\cos\theta)\right)\]
where \(\frac{Gm}{r}\) is the point mass. At \(r>a\) (a is the equatorial radius), the value of the fraction decreases. The ellipticity, \(J_2\) is the value of \(J_{2\ell}\) when \(\ell = 1\) and is the largest term in the summation.



