3.7: Flow Separation
- Page ID
- 4806
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The overall pattern of flow at fairly high Reynolds numbers past blunt bodies or through sharply expanding channels or conduits is radically different from the pattern expected from inviscid theory, which I have said is often a good guide to the real flow patterns. Figure \(\PageIndex{1}\) shows two examples of such flow patterns, one for a sphere and one for a duct or pipe that has a downstream expansion at some point. Near the point where the solid boundary begins to diverge or fall away from the direction of the mean flow, the boundary layer separates or breaks away from the boundary. This phenomenon is called flow separation.
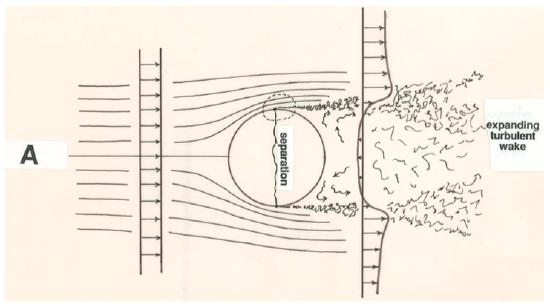
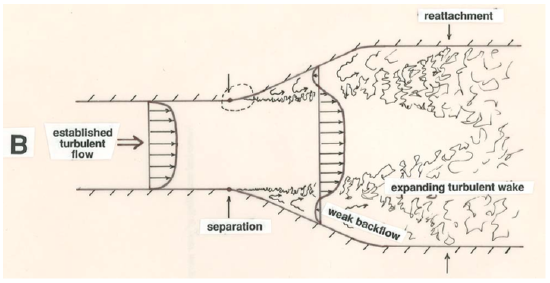
In all cases the flow separates from the boundary in such a way that the fluid keeps moving straight ahead as the boundary surface falls away from the direction of flow just upstream. The main part of the flow, outside the boundary layer, diverges from the solid boundary correspondingly. If you look only at the regions enclosed by the dashed curves in Figure \(\PageIndex{1}\) you can appreciate that flow separation is dependent not so much on the overall flow geometry as on the change in the orientation of the boundary relative to the overall flow—a change that involves a curving away of the boundary from the overall flow direction. Separation takes place at or slightly downstream of the beginning of this curving away.
The region downstream of the separation point is occupied by stagnant fluid with about the same average velocity as the boundary itself. In this region the fluid has an unsteady eddying pattern of motion, with only a weak circulation as shown in Figure \(\PageIndex{1}\). As soon as the boundary layer leaves the solid boundary it is in contact with this slower-moving fluid across a surface of strong shear. This surface of shearing is unstable, and a short distance downstream of the separation point it becomes wavy and then breaks down to produce turbulence. This turbulence is then mixed or diffused both into the main flow and into the stagnant region, and it is eventually damped out by viscous shearing within eddies, but its effect extends for a great distance downstream. The stagnant region of fluid inside the separation surface, together with the region of strong turbulence developed on the separation surface, is called a wake. Far downstream from a blunt body like a sphere (Figure \(\PageIndex{1}\)A) the wake turbulence is weak and the average fluid velocity along a profile across the mean flow is slightly less than the free-stream velocity. In flow past an expansion in a duct or channel (Figure \(\PageIndex{1}\)B), the expanding zone of wake turbulence eventually impinges upon the boundary; downstream of this point, where the flow is said to reattach to the boundary, the flow near the boundary is once again in the downstream direction, and a new boundary layer develops until far downstream of the expansion the flow is once again fully established.
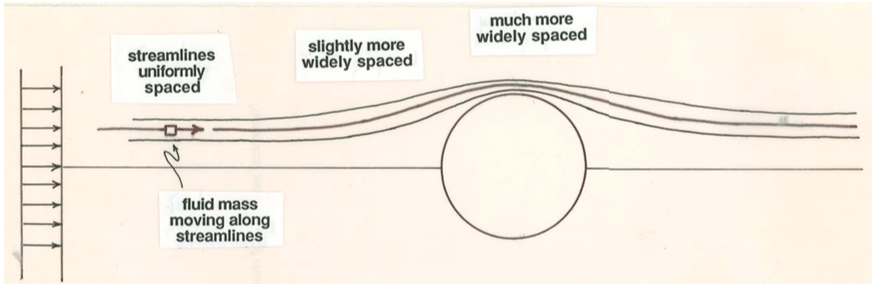
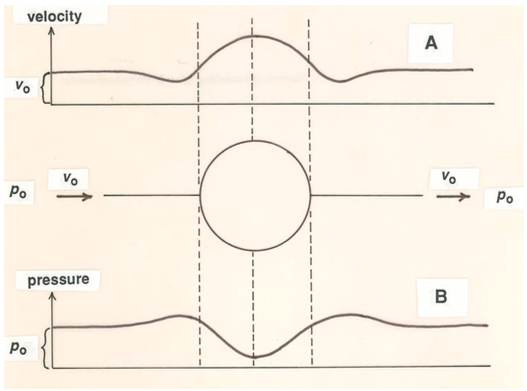
You can understand why flow separation takes place by reference to steady inviscid flow around a sphere (Figure \(\PageIndex{2}\)). Remember that variations in fluid velocity can be deduced qualitatively just from variations in spacing of neighboring streamlines. As a small mass of fluid approaches the sphere along a streamline that will take it close to the surface of the sphere, it decelerates slightly from its original uniform velocity and then accelerates to a maximum velocity at the midsection of the sphere (Figure \(\PageIndex{3}\)A). Beyond the midsection it experiences precisely the reverse variation in velocity: it decelerates to minimum velocity and then accelerates slightly back to the free-stream velocity. We can apply the Bernoulli equation (Equation 3.4.7 or 3.4.8) to find the corresponding variation in fluid pressure (Figure \(\PageIndex{3}\)B). The pressure is slightly greater than the free-stream value at points just upstream and just downstream of the sphere but shows a minimum at the midsection. It is this variation in pressure that causes strong accelerations and decelerations as the fluid passes around the sphere. In front of the sphere the pressure decreases along the streamline (the spatial rate of change or gradient of pressure is said to be negative or favorable), so there is a net force on the fluid mass in the direction of motion, causing an acceleration. In back of the sphere the pressure increases along the streamline (the pressure gradient is positive or adverse), so there is a net force opposing the motion, and the fluid mass decelerates.
In inviscid flow the pressure is the only force in the fluid. But in the real world of viscous fluids, a boundary layer develops next to the sphere (Figure \(\PageIndex{4}\)). If the boundary layer is thin, the streamwise variation in fluid pressure given by the Bernoulli equation along streamlines just outside the boundary layer is approximately the same as the pressure on the boundary; the pressure outside the boundary layer is said to be impressed on the boundary. If now you follow the motion of a fluid mass along a streamline that is close enough to the sphere to become involved in the boundary layer, a viscous force as well as the impressed pressure force acts on the fluid mass. Because the viscous force everywhere opposes the motion, the fluid mass cannot ultimately regain its uniform velocity after passing the sphere, as in inviscid flow. The fluid cannot accelerate as much in front of the sphere as in the inviscid flow, and it reaches the midsection with lower velocity; then the adverse pressure gradient in back of the sphere, which is augmented by the viscous retardation, decelerates the fluid to zero velocity and causes it to start to move in reverse. This reverse flow forms a barrier to the continuing flow from the front of the sphere, and so the flow must break away from the boundary to pass over the obstructing fluid. Because velocities are small along streamlines close to the boundary, this deceleration to zero velocity occurs only a short distance downstream of the onset of the adverse pressure gradient where the boundary curves away from the mean flow direction.
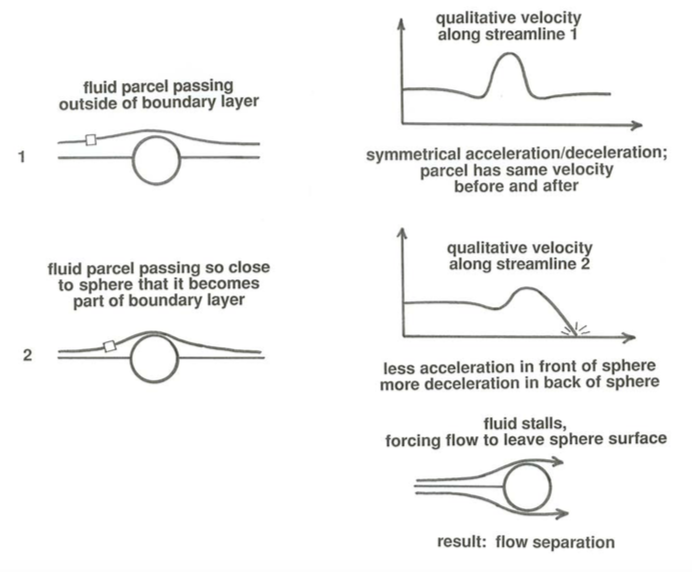
Once the separated flow is established, the flow pattern looks something like that shown in Figure \(\PageIndex{5}\). This figure is just a detail of the region enclosed by the dashed curves in Figure \(\PageIndex{1}\).

You might justifiably ask why this same explanation should not hold just as well for slow flow around a sphere at Reynolds numbers small enough to be in the Stokes range. A superficial answer would be that according to Stokes’ law for slow viscous flow around a sphere the distributions of pressure and shear stress are such that the flow passes around the sphere without reversal. A more basic explanation, which is qualitatively true but may not be very helpful, is as follows. As noted earlier in this chapter, flow around a sphere at low velocities is characterized by fluid accelerations that are everywhere so small compared to fluid velocities that the viscous forces are everywhere closely balanced by pressure forces, so that there is no tendency for fluid to decelerate to a stall. At these low velocities, retardation by viscous shearing in the fluid caused by the presence of the solid boundary extends for a great distance away from the surface of the sphere. As the velocity around the sphere increases, this retarded fluid is to a progressively greater extent swept or advected back around the sphere, to be “replaced” by faster-moving fluid, thus concentrating the region of retardation into a relatively thin layer near the solid boundary. The pressure distribution in the fluid outside this thin boundary layer becomes more and more like that predicted by inviscid theory. Think in terms of a balance between spreading of retardation outward from the solid boundary, on the one hand, and delivery of faster-moving fluid from upstream, on the other hand. As the Reynolds number increases, the latter effect becomes more and more important relative to the former. Ultimately, flow separation develops for the reasons outlined above.


