3.4: The Bernoulli Equation
- Page ID
- 4165
In the example of inviscid flow past a sphere described in the preceding section, the pressure is high at points where the velocity is low, and vice versa. It is not difficult to derive an equation, called the Bernoulli equation, that accounts for this relationship. Because this will be useful later on, I will show you here how it comes about.
Flowlines
First I have to be more specific about what I have casually been calling flow lines. Fluid velocity is a vector quantity, and, because the fluid behaves as a continuum, a velocity vector can be associated with every point in the flow. (Mathematically, this is described as a vector field.) Continuous and smooth curves that can be drawn to be everywhere tangent to the velocity vectors throughout the vector field are called streamlines (Figure \(\PageIndex{1}\)). One and only one streamline passes through each point in the flow, and at any given time there is only one such set of curves in the flow. There obviously is an infinity of streamlines passing through any region of flow, no matter how small; usually only a few representative streamlines are shown in sketches and diagrams. An important property of streamlines follows directly from their definition: the flow can never cross streamlines.
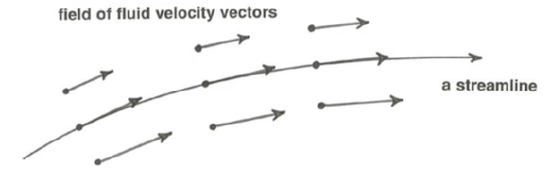
If the flow is steady, the streamline pattern does not change with time; if the streamline pattern changes with time, the flow is unsteady. But note that the converse of each of these statements is not necessarily true, because an unsteady flow can exhibit an unchanging pattern of streamlines as velocities everywhere increase or decrease with time.
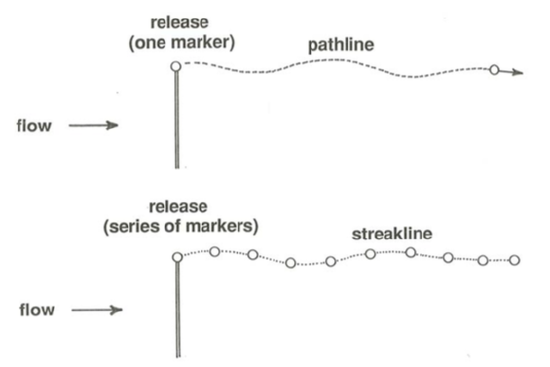
There are two other kinds of flow lines, with which you should not confuse streamlines (Figure \(\PageIndex{2}\)): pathlines, which are the trajectories traced out by individual tiny marker particles emitted from some point within the flow that is fixed relative to the stationary boundaries of the flow, and streaklines, which are the streaks formed by a whole stream of tiny marker particles being emitted continuously from some point within the flow that is fixed relative to the stationary boundaries of the flow. In steady flow, streamlines and pathlines and streaklines are all the same; in unsteady flow, they are generally all different.
Streamtubes and the Bernoulli Equation
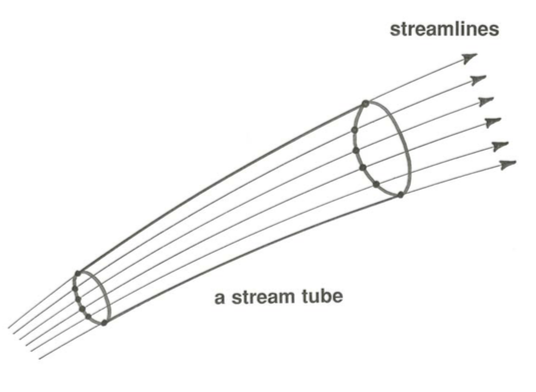
You also can imagine a tube-like surface formed by streamlines, called a stream tube, passing through some region (Figure \(\PageIndex{3}\)). This surface or set of streamlines can be viewed as functioning as if it were a real tube or conduit, in that there is flow through the tube but there is no flow either inward or outward across its surface.
Consider a short segment of one such tiny stream tube in a flow of incompressible fluid (Figure \(\PageIndex{4}\)). Write the equation of motion (Newton’s second law) for the fluid contained at some instant in this stream-tube segment. The cross-sectional area of the tube is \(\Delta A\), and the length of the segment is \(\Delta s\). If the pressure at cross section 1, at the left-hand end of the segment, is \(p\), then the force exerted on this end of the segment is \( p \Delta A\). It is not important that the area of the cross section might be slightly different at the two ends (if the flow is expanding or contracting), or that \(p\) might vary slightly over the cross section, because you can make the cross-sectional area of the stream tube as small as you please. What is the force on the other end of the tube? The pressure at cross section 2 is different from that at cross section 1 by \((\partial p / \partial s) \Delta s\), the rate of change of pressure in the flow direction times the distance between the two cross sections, so the force on the right-hand end of the tube is
\[\left(p+\frac{\partial p}{\partial s} \Delta s\right) \Delta A \label{3.7} \]
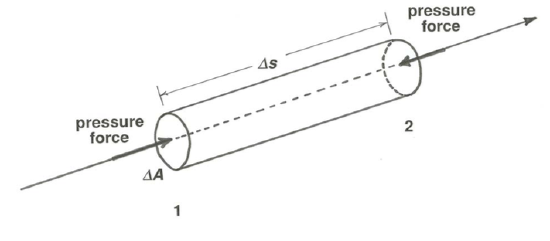
The net force on the stream tube in the flow direction is then
\[p \Delta A-\left(\mathrm{p}+\frac{\partial p}{\partial s} \Delta s\right) \Delta A=-\frac{\partial p}{\partial s} \Delta s \Delta A \label{3.8} \]
The pressure on the lateral surface of the tube is of no concern, because the pressure force on it acts normal to the flow direction.
Newton’s second law, \(F = d(m v) / d t\) , for the fluid in the segment of the stream tube, where \(v\) is the velocity of the fluid at any point (in this section \(v\) is used not as the component of velocity in the \(y\) direction but as the component of velocity tangent to the streamline at a given point), is then
\[-\frac{\partial p}{\partial s} \Delta s \Delta A=\frac{d}{d t}[v(\rho \Delta s \Delta A)] \label{3.9} \]
Simplifying Equation \ref{3.9} and making use of the fact that \(\rho\) is constant and so can be moved outside the derivative,
\[-\frac{\partial p}{\partial s}=\rho \frac{d v}{d t} \label{3.10} \]
The derivative on the right side of Equation \ref{3.10} can be put into more convenient form by use of the chain rule and a simple “undifferentiation” of one of the resulting terms:
\[\begin{aligned}-\frac{\partial p}{\partial s} &=\rho \frac{d v}{d t} \\ &=\rho\left[\frac{\partial v}{\partial t} \frac{d t}{d t}+\frac{\partial v}{\partial s} \frac{d s}{d t}\right] \\ &=\rho\left[\frac{\partial v}{\partial t}+v \frac{\partial v}{\partial s}\right] \end{aligned}\]
\[=\rho\left[\frac{\partial v}{\partial t}+\frac{1}{2} \frac{\partial\left(v^{2}\right)}{\partial s}\right] \label{3.11} \]
Equation \ref{3.11} is strictly true only for the single streamline to which the stream tube collapses as we let \(\Delta A\) go to \(0\), because only then need we not worry about possible variation of either \(p\) or \(v\) over the cross sections. Assuming further that the flow is steady, \(\partial v / \partial t=0\), and Equation \ref{3.11} becomes
\[-\frac{\partial p}{\partial s}=\frac{\rho}{2} \frac{\partial\left(v^{2}\right)}{\partial s} \label{3.12} \]
It is easy to integrate Equation \ref{3.12} between two points \(1\) and \(2\) on the streamline (remember that this equation holds for any streamline in the flow):
\(-\int_{1}^{2} \frac{\partial p}{\partial s} d s=\frac{\rho}{2} \int_{1}^{2} \frac{\partial\left(v^{2}\right)}{\partial s} d s\)
\[p_{2}-p_{1}=-\frac{\rho}{2}\left(v_{2}^{2}-v_{1}^{2}\right) \label{3.13} \]
or, viewed in another way,
\[p+\frac{\rho v^{2}}{2}= \text {const} \label{3.14} \]
You can see from Equation \ref{3.13} that if the flow is steady and incompressible there is an inverse relationship between fluid pressure and fluid velocity along any streamline. Equation \ref{3.13} or Equation \ref{3.14} is called the Bernoulli equation. Remember that it holds only along individual streamlines, not through the entire flow. In other words, the constant in the Equation \ref{3.14} is generally different for each streamline in the flow. And it holds only for inviscid flow, because if the fluid is viscous there are shearing forces across the lateral surfaces of stream tubes, and Newton’s second law cannot be written and manipulated so simply. But often in flow of a real fluid the viscous forces are small enough outside the boundary layer that the Bernoulli equation is a good approximation.
Note
Note that the right-hand side of Equation \ref{3.13} is the negative of the increase in kinetic energy per unit volume of fluid between point 1 and point 2. The Bernoulli equation is just a statement of the work–energy theorem, whereby the work done by a force acting on a body is equal to the change in kinetic energy of the body. In this case, fluid pressure is the only force acting on the fluid.
In discussing inviscid flow around a sphere I called the front and rear points of the sphere the stagnation points, because velocities relative to the sphere are zero there. Using the Bernoulli equation it is easy to find the corresponding stagnation pressures. Taking the free-stream values of pressure and velocity to be po and vo, writing Equation \ref{3.13} in the form
\[p-p_{o}=-\frac{\rho}{2}\left(v^{2}-v_{o}^{2}\right) \label{3.15} \]
and substituting \(v = 0\) at the stagnation points, the stagnation pressures (the same for front and rear points) are
\[p=p_{o}+\frac{\rho v_{o}^{2}}{2} \label{3.16} \]


