3.3: Inviscid Flow
- Page ID
- 4164
Over the past hundred and fifty years a vast body of mathematical analysis has been devoted to a kind of fluid that exists only in the imagination: an inviscid fluid, in which no viscous forces act. This fiction (in reality there is no such thing as an inviscid fluid) allows a level of mathematical progress not possible for viscous flows, because the viscous-force term in the Navier–Stokes equation disappears, and the equation becomes more tractable. The major outlines of mathematical analysis of the resulting simplified equation, which is mostly beyond the scope of these notes, were well worked out by late in the 1800s. Since then, fluid dynamicists have been extending the results and applying or specializing them to problems of interest in a great many fields.
Fluid Velocity for Inviscid Flow
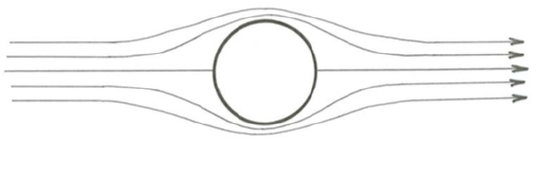
The pattern of inviscid flow around a sphere, obtained as noted above by solving the equation of motion for inviscid flow, is shown in Figure \(\PageIndex{1}\). The arrangement of flow lines differs significantly from that in creeping viscous flow around the sphere (Figure 3.2.1): the symmetry is qualitatively the same, but, in contrast to creeping flow, the flow lines become more closely spaced around the midsection, reflecting acceleration and then deceleration of the flow as it passes around the sphere. Figure \(\PageIndex{2}\) is a plot of fluid velocity along the particular flow line that meets the sphere at its front point, passes back along the surface of the sphere, and leaves the sphere again at the rear point. The velocity varies symmetrically with respect to the midsection of the sphere: it falls to zero at the front point, accelerates to a maximum at the midsection, falls to zero again at the rear point, and then attains its original value again downstream. The front and rear points are called stagnation points, because the fluid velocity is zero there. Note that elsewhere the velocity is not zero on the surface of the sphere, as it is in viscous flow. Do not let this unrealistic finite velocity on the surface of the sphere bother you; it is a consequence of the unrealistic assumption that viscous effects are absent, so that the no-slip condition is not applicable.

Fluid Pressure for Inviscid Flow
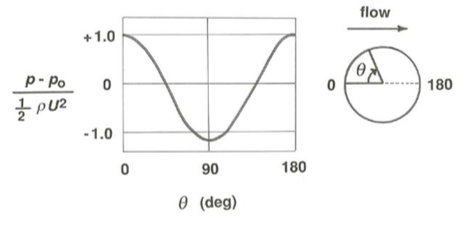
Figure \(\PageIndex{3}\) shows the distribution of fluid pressure around the surface of a sphere moving relative to an inviscid fluid. As with velocity, pressure is distributed symmetrically with respect to the midsection, and its variation is just the inverse of that of the velocity: relative to the uniform pressure far away from the sphere, it is greatest at the stagnation points and least at the midsection. One seemingly ridiculous consequence of this symmetrical distribution is that the flow exerts no net pressure force on the sphere, and therefore, because there are no viscous forces either, it exerts no resultant force on the sphere at all! This is in striking contrast to the result noted above for creeping viscous flow past a sphere (Figure 3.2.3), in which the distribution of pressure on the surface of the sphere shows a strong front-to-back asymmetry; it is this uneven distribution of pressure, together with the existence of viscous shear forces on the boundary, that gives rise to the drag force on a sphere in viscous flow.
Value of Inviscid Theory
So the distributions of velocity and pressure in inviscid flow around a sphere, and therefore of the fluid forces on the sphere, are grossly different from the case of flow of viscous fluid around the sphere. Then what is the value of the inviscid approach? You will see in the section on flow separation later on that at higher real-fluid velocities the boundary layer in which viscous effects are concentrated next to the surface of the sphere is thin, and outside this thin layer the flow patterns and the distributions of both velocity and pressure are approximately as given by the inviscid theory. Moreover, the boundary layer is so thin for high flow velocities that the pressure on the surface of the sphere is approximately the same as that given by the inviscid solution just outside the boundary layer. And because at these high velocities the pressure forces are the main determinant of the total drag force, the inviscid approach is useful in dealing with forces on the sphere after all. Behind the sphere the flow patterns given by inviscid theory are grossly different from the real pattern at high Reynolds numbers, but you will see that one of the advantages of the inviscid assumption is that it aids in a rational explanation for the existence of this great difference.
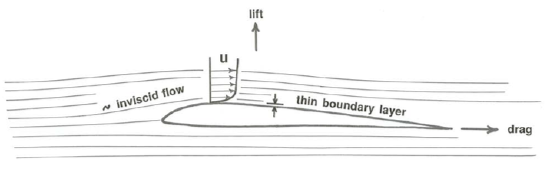
In many kinds of flows around well streamlined bodies like airplane wings, agreement between the real viscous case and the ideal inviscid case is much better than for flow around blunt or bluff bodies like spheres. In flow of air around an airplane wing, viscous forces are important only in a very thin layer immediately adjacent to the wing, and outside that layer the pressure and velocity are almost exactly as given by inviscid theory (Figure \(\PageIndex{4}\)). It is these inviscid solutions that allow prediction of the lift on the airplane wing: although drag on the wing is governed largely by viscous effects within the boundary layer, lift is largely dependent upon the inviscid distribution of pressure that holds just outside the boundary layer. To some extent this is true also for flow around blunt objects resting on a planar surface, like sand grains on a sand bed under moving air or water.