8.3: Particle Motions vs. Turbulence

A few qualitative observations on the effect of a turbulent flow field on the motions of suspended particles might be useful here, to set the stage for later chapters.

Think about a sediment particle in a turbulent fluid. Clearly, its trajectory will be sinuous rather than straight, and its velocity will be irregular rather than constant. The particle undergoes two kinds of accelerations at the same time:

1. temporal accelerations, because the velocity varies with time at points the particle happens to occupy; and
2. spatial accelerations, because the particle falls through regions with different fluid velocity.

Physical effects, partly related, that we have to consider are the following. Details on some of these effects are given in later paragraphs.

• Relative inertia
• Particle size relative to eddy size
• Turbulent velocity fluctuations relative to particle velocity
• The effect of acceleration on the drag force

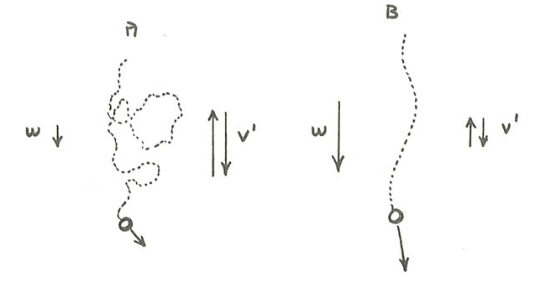
The effect of relative inertia is expressed by the ratio \(\rho_{s} /\rho \). For \(\rho_{s}/ \rho >> 1\), the much greater inertia of the particle causes its trajectory to be relatively little affected by the turbulence (Figure \(\PageIndex{1}\)A). For \(\rho_{s}/\rho \approx 1\), on the other hand, the approximately equal inertia of the particle and the fluid causes the trajectory of the particle to be strongly affected by the turbulence (Figure \(\PageIndex{1}\)B). This effect is independent of the weight of the particle: in an extraterrestrial place with very small \(g\), a particle can have a small immersed specific weight \(\gamma^{\prime}\) but large \(\rho_{s}/\rho\), whereas in an extraterrestrial place with very large \(g\), a particle can have a large \(\gamma^{\prime}\) but small \(\rho_{s}/\rho\). On the Earth, however, weight and relative inertia are unavoidably linked.

Figure \(\PageIndex{1}\): The effect of relative particle inertia when a particle moves through a turbulent fluid. A) Relative inertia is high; B) relative inertia is low.

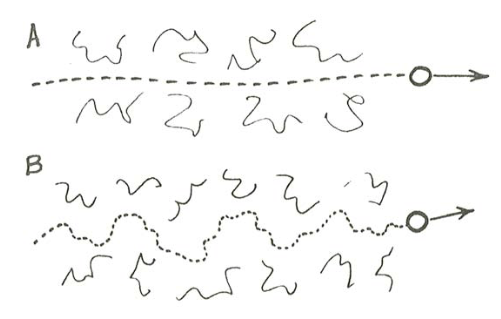
If the sediment particle is much larger than the turbulent eddies, then small eddies distort the local velocity field near the surface of the particle and affect the drag force on the particle, but the motion of the particle is not much affected (Figure \(\PageIndex{2}\)A). If the particle is much smaller than the surrounding eddies, however, the particle senses a nearly uniform but unsteady fluid acceleration in its vicinity; the curvature of the particle trajectory is large relative to particle size (Figure \(\PageIndex{2}\)B).

Figure \(\PageIndex{2}\): The effect of particle size relative to eddy size. A) The particles are much larger than the eddies. B) The particles are smaller than the maximum eddy size.

 

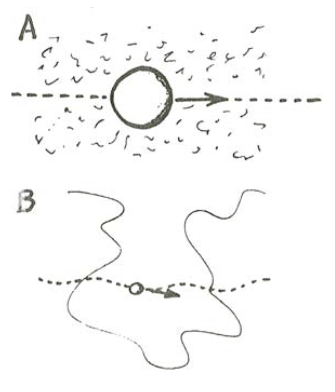
The effect of turbulent velocity fluctuations relative to particle velocity is especially relevant to settling particles. If the vertical turbulent velocity fluctuations are much greater than the settling velocity of the particle, then the particle has a highly sinuous trajectory, with frequent reversals of its vertical velocity component (Figure \(\PageIndex{3}\)A). If the vertical turbulent velocity fluctuations are much less than the settling velocity of the particle, however, then the settling velocity is little affected by turbulence: the fall is always downward, the speed of the particle relative to the bottom varies only slightly, and the path of settling is only slightly sinuous (Figure \(\PageIndex{3}\)B).

Figure \(\PageIndex{3}\): Effect of particle settling velocity relative to turbulent velocity fluctuations. A) The particle settles slowly relative to the vertical velocity fluctuations. B) The particle settles rapidly relative to the vertical velocity fluctuations.

 

What was done in Chapters 2 and 3 in Part 1 on the drag force on a sphere was predicated upon steady flow. When the local fluid velocity around the sphere is changing, the drag force is in general different from that predicted for a uniform relative velocity of the same value, because the local patterns of velocity and fluid pressure lag behind the changing free-stream flow velocity.