7.1: Playing on a Rotating Table

Introduction

In everything up to now in these notes, we have assumed that the flow environment is stationary. Just think back to flow around a sphere or flow down a channel. And even if the flow environment is in uniform motion, relative to you as the observer, you have already seen that you can convert the problem to that of a stationary flow environment just by moving with flow environment itself; think back to the problem of relative motion of a sphere and an ambient fluid.

But what if the flow environment is accelerating? That turns out to be quite a different matter. This chapter examines some of the effects of steady rotation of the flow environment. (Remember that rotation involves acceleration, of the radial rather than the tangential kind, even with a steady rotation rate.) The effects of rotation on the flow are striking, and I think not intuitive. These effects are of central importance in the study of what are called geophysical flows: the movements of the atmosphere and the oceans on scales of hundreds and thousands of kilometers. The boundaries of these flows are the rotating solid Earth, and we the observers are rotating with that solid Earth. Admittedly, the effects of rotation do not have a very direct bearing on the small-scale dynamics of sediment transport, but the indirect consequences are so far-reaching that I could not resist including this chapter in these notes.

Playing on a Rotating Table

In a large unobstructed indoor area (a gymnasium or a warehouse would be best, but a big room in your house would suffice), build a giant flat horizontal turntable—just a disk mounted at its center point on a vertical rotating shaft (Figure \(\PageIndex{1}\)). You can rotate the whole disk at any desired constant rotation rate, described by its angular velocity \(\gamma\), measured in radians per second. It would be best if you painted the surface of the disk a flat black, the better to observe the motions of the brilliantly white marker spheres you are going to roll around on the surface. To make things really exciting, be sure to coat the white marker spheres with a thick chalky coating of some sort that tracks off evenly onto the surface of the turntable as the spheres roll about.

Figure \(\PageIndex{1}\): Playing on a rotating table.

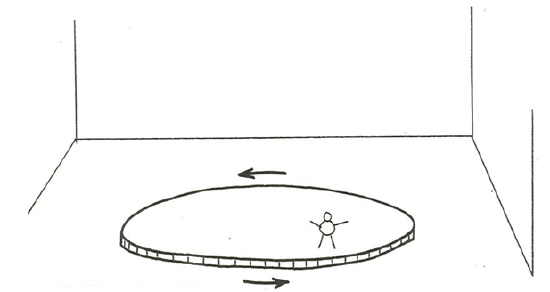
To do things right, you are also going to need an observation perch above the turntable. This perch should be easily movable from place to place above the surface, but (and this is important) stationary relative to the floor of the room while it is in use. One of those mechanized cherry-picker seats, extending horizontally from the margin of the disk, would do nicely, if you can afford it.

Set the rotation rate, settle into your perch, occupy a point just over the turntable, and roll one of your marked spheres onto the table, just as if you were at a bowling alley. Here is the big question: What would the track of the sphere look like on the turntable? (You are going to have to assume that the turntable exerts no substantial force on the rolling ball. That is not really true, but the effects are small enough that you can safely ignore them for the purposes of this demonstration. If you are uncomfortable with that assumption, you can always imagine a magic air-hockey puck that scoots nearly frictionlessly over the turntable, leaving a powdery white trail behind it.)

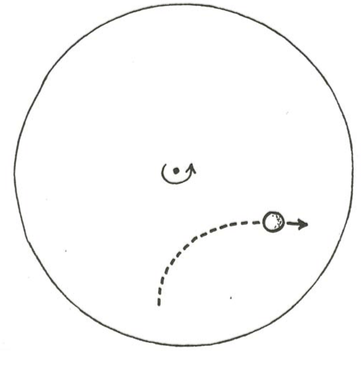
The big jump that your powers of deduction or imagination have to take here is to see that the track left by the ball on the table would be curved (Figure \(\PageIndex{2}\)). And, once you are comfortable with that idea, it might naturally occur to you to think about whether that curved track is a circular arc. The answer turns out to be NO, although the reasons are a bit too intricate to deal with at the moment.

Figure \(\PageIndex{2}\): The track left by a ball rolling on a rotating table.

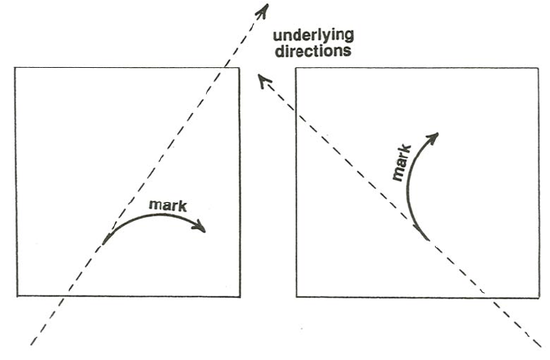
If you cannot afford the time and money to build the turntable but you still want to get some results, here is a simpler and much less expensive way of demonstrating the phenomenon (Figure \(\PageIndex{3}\)). Pin a big piece of posterboard to the wall so that it can be rotated about its center point, and have an assistant stand to one side and rotate the posterboard in a hand-over-hand motion as steadily as possible. Stand on one side of the posterboard with a marker pen, and draw a line on the posterboard in such a way that the tip of the pen moves in uniform rectilinear motion relative to the underlying wall. That is not easy to do, because you need to try to ignore the surface of the posterboard, and the mark that is being made on it, and instead concentrate on the imaginary path of the pen point on the motionless wall behind. You would find (Figure \(\PageIndex{4}\)) that no matter where you start on the posterboard, and no matter which direction you choose for your line, the mark on the posterboard will be an arc, not a straight line!

Figure \(\PageIndex{3}\): How to show that the track of an object moving in a straight line looks curved from the viewpoint of an observer in a rotating frame of reference.

Figure \(\PageIndex{3}\).

You do not even need to rig up such a posterboard exercise, really; just think about your rapidly obsolescing phonograph. Pretend that the needle that passively follows the groove in the record is in fact constrained to move from the edge of the record to the center of the record in an almost straight line relative to the underlying stationary phonograph structure. The needle makes a spiral path on the record, with curvature as described in the two foregoing experiments.

And incidentally, this phonograph exercise shows conclusively that the curving arc is not exactly circular: the curvature is tighter along parts of the path located closer to the axis of rotation. That is basically because the velocity of the moving object (the needle) relative to the rotating surface (the record) decreases as the needle makes its way toward the center of the record. Why? Because the speed of the needle relative to the fixed stars is constant but the velocity of points on the record increases from zero at the center to a maximum at the outer edge.

But back to the big turntable: have your assistant roll a marker sphere onto the turntable while you are riding on the turntable. Watch the ball as it rolls and leaves its curving track. It will look to you as though some mysterious sideways force is continuously acting on the ball normal to its path to push it off its course. Something seems to be wrong with Newton’s first law, which tells you that the ball should be moving in a straight line at constant speed. You know what the problem is, of course: the fictitious side force is an artifact of your observation of the ball from the standpoint of the rotating turntable. If you reoccupied your perch and rolled a clean, bright, chalkless ball onto the dimly lit black surface of the turntable, you would see the ball roll in a nice straight line! The fictitious side force that seems to act on moving bodies in a rotating environment is called the Coriolis force, after the nineteenth-century French mathematician who first analyzed the effect. And the apparent acceleration of the sphere (it is a radial acceleration, not a tangential acceleration, in that only the direction changes, not the speed) is called the Coriolis acceleration. The entire effect is called the Coriolis effect.

What is the relevance of this demonstration to the motion of fluids? You could produce all kinds of fluid flows right on the surface of that turntable, by using that surface as your fluid dynamics laboratory: flow in an open channel, a free-convective flow in a big dishpan, or even just a sheet of water flowing freely across the surface of the turntable. In each case, every tiny element of the flowing fluid is subjected to that same Coriolis force. For the right combinations of fluid speeds and rotation rates, the Coriolis effect would have profound consequences for the pattern of fluid movement.