1.12: Understanding Maps

Understanding Maps

Maps are perhaps the most important tools for navigation and evaluating features on the land's surface, underwater, or even underground. Maps are used for many issues involving land use and natural resource management. Maps have been used back into prehistoric times. However, the evolution of maps in the modern digital world has changed map making—enhancing their use in nearly all aspects of modern science, technology, and culture. Modern maps are created with geographic information systems (GIS). A GIS is a computer-based map-generating program that can merge geographic (spatial) information with many kinds of topical themes in database format. Such themes may consist of medical information (such as disease outbreak data), water resources, roads, buildings and civic infrastructure, power grid information, agricultural and biological information, etc.). Satellite data are increasingly used for nearly all aspects of mapping of the land, oceans, and weather patterns.

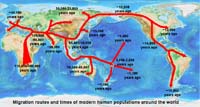
Figure 1.29. Maps show thematic information in a geographic context. The theme of this map shows human migration routes on a world map base.

Many maps display relief or elevation information . Relief relates to height and shape characteristics of a landscape (such as high relief, low, relief, gentle relief, rugged relief, etc. Shaded-relief maps show changes in elevation (topography and bathymetry) using shades of gray or color.

What are Latitude and Longitude?

Locations on the Earth's surface are defined using latitude and longitude coordinate system (Figure 1.30).

Latitude is the angular distance of a place north or south of the earth's equator, usually expressed in degrees and minutes. Lines of latitude are called parallels. Latitude lines parallel the Equator. Each degree of latitude is approximately 69 miles (111 kilometers) apart. Latitude in the Northern Hemisphere can be determined by sighting on the North Star (which lies directly above the North Pole) and determining the angle of the star above the horizon (subtract it from 90°).

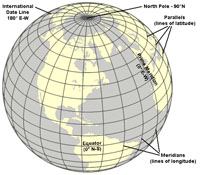Longitude is the angular distance of a place east or west of the Prime Meridian usually expressed in degrees and minutes. In order to make an accurate map of the stars for use in ship navigation, in 1884, a location indicating the precise location of 0° East-West was designated in the cross hairs of a telescope in the Royal Observatory (now located on the grounds of the National Maritime Museum) in Greenwich England. This line marks the reference location of the Prime Meridian now used in all global mapping (including GPS location systems). The International Date Line is on the opposite side of the earth located 180° east or west of the Prime Meridian.

Figure 1.30. Longitude and Latitude projected on a globe

A meridian is a circle of constant longitude passing through a given place on the earth's surface and the terrestrial poles. Longitude lines (of equal spacing measured in degrees) are widely spaced at the equator but converge at point at the North and South Poles. The Prime Meridian is designated 0° (zero degrees). Meridian lines east of the Prime Meridian are designated positive values (0° to 180° east); whereas meridian lines west of the Prime Meridian are designated negative values (-0° to -180°). At 180° east or west is the International Date Line. A degree of longitude is widest at the equator at 69.172 miles (111.321) and gradually shrinks to zero at the poles. At 40° north or south the distance between a degree of longitude is 53 miles (85 km).

Defining locations with a latitude-longitude coordinate system—any location on the planet surface can be defined by a number in degrees, minutes, and seconds north or south of the Equator and east or west of the Prime Meridian. (Compare to hours, minutes, seconds on a clock!)

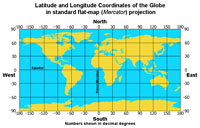
Figure 1.31. Map of the world showing latitude and longitude in a Mercator (flat) projection

Figure 1.32. Map of world showing with Mercator Projection - notice distortion in high latitudes because longitude lines are not converging

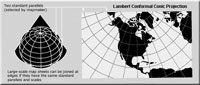
Figure 1.33. Map of North America with Lambert Conic Projection - on this scale distortion of America is minimal, but look at South America.

Example: Location of the Statue of Liberty in New York Harbor

The standard coordinates (in degrees, minutes, and seconds) of the Statue of Liberty are:
Latitude: 40°68′92"N
Longitude: 74°04′ 45"W.

Described in decimal degrees the coordinates of the Statue of Liberty are:
Latitude: 40.689758° N
Longitude:-74.045138° W.

An example from San Diego, California
The monument on top of Mount Soledad in La Jolla is located:
Latitude: 32.8398° N
Longitude: 117.2523° W.

Fig. 34. A globe view is the only way to have perfect map projection!

Find the latitude and longitude of any named location or landscape feature on the GeoNames website.

The earth is round (a sphere like a globe) but maps are flat. As a result, maps that show large regions are distorted. Map projections are attempts to portray a portion of the Earth on a flat surface (examples are shown in Figures 1-31 to 1-33). The flattening of a map always causes some distortions of distance, direction, scale, and area. Large scale maps (such as a map of a continent or a world show much distortion, however, maps on small scales (such as a map of a town or neighborhood) have relatively little distortion. There are many map projection systems, each serves different purposes and has some variety of distortion. Learn more about map projections at the U.S. Geological Survey's Map Projections website.

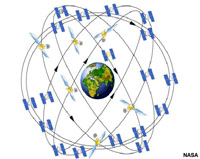A Global Positioning System (GPS) is a space-based global navigation satellite system that provides reliable location and time information in all weather and at all times and anywhere on or near the Earth when and where there is an unobstructed line of sight to four or more GPS satellites (Figure 1.35). GPS is now used for nearly all forms of digital map navigation.

Figure 1.35. Satellite network of the Global Positioning System.