14.2: Variable Equatorial Circulation: El Niño/La Niña

The trades are remarkably steady, but they do vary from month to month and year to year, especially in the western Pacific. One important source of variability are Madden-Julian waves in the atmosphere (McPhaden, 1999). If the trades in the west weaken or reverse, the air-sea system in the equatorial regions can be thrown into another state called El Niño. This disruption of the equatorial system in the Pacific is the most important cause of changing weather patterns around the globe.

Although the modern meaning of the term El Niño denotes a disruption of the entire equatorial system in the Pacific, the term has been used in the past to describe several very different processes. This causes a lot of confusion. To reduce the confusion, let’s learn a little history.

A Little History

In the 19th century, the term was applied to conditions off the coast of Peru. The following quote comes from the introduction to Philander’s (1990) excellent book El Niño, La Niña, and the Southern Oscillation:

In the year 1891, Señor Dr. Luis Carranza of the Lima Geographical Society contributed a small article to the Bulletin of that Society, calling attention to the fact that a counter-current flowing from north to south had been observed between the ports of Paita and Pacasmayo.

The Paita sailors, who frequently navigate along the coast in small craft, either to the north or the south of that port, name this countercurrent the current of “El Niño” (the Child Jesus) because it has been observed to appear immediately after Christmas.

As this counter-current has been noticed on different occasions, and its appearance along the Peruvian coast has been concurrent with rains in latitudes where it seldom if ever rains to any great extent, I wish, on the present occasion, to call the attention of the distinguished geographers here assembled to this phenomenon, which exercises, undoubtedly, a very great influence over the climatic conditions of that part of the world.— Señor Frederico Alfonso Pezet’s address to the Sixth International Geographical Congress in Lima, Peru 1895.

The Peruvians noticed that in some years the El Niño current was stronger than normal, it penetrated further south, and it is associated with heavy rains in Peru. This occurred in 1891 when, again quoting from Philander’s book,

…it was then seen that, whereas nearly every summer here and there there is a trace of the current along the coast, in that year it was so visible, and its effects were so palpable by the fact that large dead alligators and trunks of trees were borne down to Pacasmayo from the north, and that the whole temperature of that portion of Peru suffered such a change owing to the hot current that bathed the coast. …—Señor Frederico Alfonso Pezet.

…the sea is full of wonders, the land even more so. First of all the desert becomes a garden …. The soil is soaked by the heavy downpour, and within a few weeks the whole country is covered by abundant pasture. The natural increase of flocks is practically doubled and cotton can be grown in places where in other years vegetation seems impossible.—From Mr. S.M. Scott & Mr. H. Twiddle quoted from a paper by Murphy, 1926.

The El Niño of 1957 was even more exceptional, so much so that it attracted the attention of meteorologists and oceanographers throughout the Pacific basin:

By the fall of 1957, the coral ring of Canton Island, in the memory of man ever bleak and dry, was lush with the seedlings of countless tropical trees and vines.

One is inclined to select the events of this isolated atoll as epitomizing the year, for even here, on the remote edges of the Pacific, vast concerted shifts in the ocean and atmosphere had wrought dramatic change.

Elsewhere about the Pacific it also was common knowledge that the year had been one of extraordinary climatic events. Hawaii had its first recorded typhoon; the seabird-killing El Niño visited the Peruvian coast; the ice went out of Point Barrow at the earliest time in history; and on the Pacific’s western rim, the tropical rainy season lingered six weeks beyond its appointed term—Sette and Isaacs (1960).

Just months after the event, in 1958, a distinguished group of oceanographers and meteorologists assembled in Rancho Santa Fe, California to try to understand the Changing Pacific Ocean in 1957 and 1958 (Sette and Isaacs (1960)). There, for perhaps the first time, they began the synthesis of atmospheric and oceanic events leading to our present understanding of El Niño.

While oceanographers had been mostly concerned with the eastern equatorial Pacific and El Niño, meteorologists had been mostly concerned with the western tropical Pacific, the tropical Indian Ocean, and the Southern Oscillation. Hildebrandsson, the Lockyers, and Sir Gilbert Walker noticed in the early decades of the 20th century that pressure fluctuations throughout that region are highly correlated with pressure fluctuations in many other regions of the world (figure \(\PageIndex{1}\)). Because variations in pressure are associated with winds and rainfall, they wanted to find out if pressure in one region could be used to forecast weather in other regions using the correlations.

Figure \(\PageIndex{1}\): Correlation coefficient of annual-mean sea-level pressure with pressure at Darwin. – – – – Coefficient < −0.4. After Trenberth and Shea (1987).

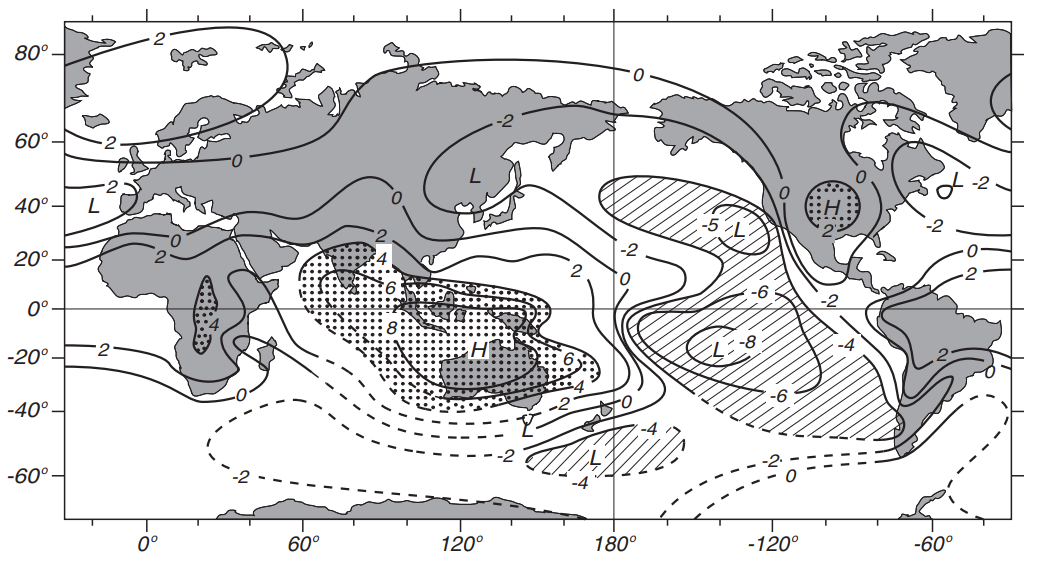
The early studies found that the two strongest centers of the variability are near Darwin, Australia and Tahiti. The fluctuations at Darwin are opposite those at Tahiti, and resemble an oscillation. Furthermore, the two centers had strong correlations with pressure in areas far from the Pacific. Walker named the fluctuations the Southern Oscillation.

The Southern Oscillation Index is sea-level pressure at Tahiti minus sea-level pressure at Darwin (figure \(\PageIndex{2}\)) normalized by the standard deviation of the difference. The index is related to the trade winds. When the index is high, the pressure gradient between east and west in the tropical Pacific is large, and the trade winds are strong. When the index is negative trades, are weak.

Figure \(\PageIndex{2}\): Correlation coefficient of annual-mean sea-level pressure with pressure at Darwin. – – – – Coefficient < −0.4. After Trenberth and Shea (1987).

The connection between the Southern Oscillation and El Niño was made soon after the Rancho Santa Fe meeting. Ichiye and Petersen (1963) and Bjerknes (1966) noticed the relationship between equatorial temperatures in the Pacific during the 1957 El Niño and fluctuations in the trade winds associated with the Southern Oscillation. The theory was further developed by Wyrtki (1975).

Because El Niño and the Southern Oscillation are so closely related, the phenomenon is often referred to as the El Niño-Southern Oscillation or ENSO. More recently, the oscillation is referred to as El Niño/La Niña, where La Niña refers to the positive phase of the oscillation when trade winds are strong, and water temperature in the eastern equatorial region is very cold.

Definition of El Niño

Philander (1990) points out that each El Niño is unique, with different temperature, pressure, and rainfall patterns. Some are strong, some are weak. So, exactly what events deserve to be called El Niño? The ICOADS data show that the best indicator of El Niño is sea-level pressure anomaly in the eastern equatorial Pacific from 4\(^{\circ}\)S to 4\(^{\circ}\)N and from 108\(^{\circ}\)W to 98\(^{\circ}\)W (Harrison and Larkin, 1996). It correlates better with sea-surface temperature in the central Pacific than with the Southern-Oscillation Index. Thus the importance of the El Niño is not exactly proportional to the Southern Oscillation Index—the strong El Niño of 1957–58 has a weaker signal in figure \(\PageIndex{2}\) than the weaker El Niño of 1965–66.

Trenberth (1997) recommends that those disruptions of the equatorial system in the Pacific shall be called an El Niño only when the 5-month running mean of sea-surface temperature anomalies in the region 5\(^{\circ}\)N–5\(^{\circ}\)S, 120\(^{\circ}\)W– 170\(^{\circ}\)W exceeds \(0.4^{\circ}\text{C}\) for six months or longer.

So El Niño, which started life as a change in currents off Peru each Christmas, has grown into a giant. It now means a disruption of the ocean-atmosphere system over the whole equatorial Pacific.

Theory of El Niño

Wyrtki (1975) gives a clear description of El Niño.

During the two years preceding El Niño, excessively strong southeast trades are present in the central Pacific. These strong southeast trades intensify the subtropical gyre of the South Pacific, strengthen the South Equatorial Current, and increase the east-west slope of sea level by building up water in the western equatorial Pacific. As soon as the wind stress in the central Pacific relaxes, the accumulated water flows eastward, probably in the form of an equatorial Kelvin wave. This wave leads to the accumulation of warm water off Ecuador and Peru and to a depression of the usually shallow thermocline. In total, El Niño is the result of the response of the equatorial Pacific to atmospheric forcing by the trade winds.

Sometimes the trades in the western equatorial Pacific not only weaken, they actually reverse direction for a few weeks to a month, producing westerly wind bursts that quickly deepen the thermocline there. The deepening of the thermocline launches an eastward-propagating Kelvin wave and a westward-propagating Rossby wave. (If you are asking “What are Kelvin and Rossby waves?”, I will answer that in a minute. So please be patient.)

The Kelvin wave deepens the thermocline as it moves eastward, and it carries warm water eastward. Both processes cause a deepening of the mixed layer in the eastern equatorial Pacific a few months after the wave is launched in the western Pacific. The deeper thermocline in the east leads to upwelling of warm water, and the surface temperatures offshore of Ecuador and Peru warms by \(2– 4^{\circ}\text{C}\). The warm water reduces the temperature contrast between east and west, further reducing the trades. The strong positive feedback between sea-surface temperature and the trade winds causes rapid development of El Niño.

Figure \(\PageIndex{3}\): Anomalies of sea-surface temperature (in \(^{\circ}\text{C}\)) during a typical El Niño obtained by averaging data from El Niños between 1950 and 1973. Months are after the onset of the event. After Rasmusson and Carpenter (1982).

With time, the warm pool spreads east, eventually extending as far as 140\(^{\circ}\)W (figure \(\PageIndex{3}\)). Plus, water warms in the east along the equator due to upwelling of warm water, and to reduced advection of cold water from the east due to weaker trade winds.

The warm waters along the equator in the east cause the areas of heavy rain to move eastward from Melanesia and Fiji to the central Pacific. Essentially, a major source of heat for the atmospheric circulation moves from the west to the central Pacific, and the whole atmosphere responds to the change. Bjerknes (1972), describing the interaction between the ocean and the atmosphere over the eastern equatorial Pacific, concluded:

In the cold ocean case (1964) the atmosphere has a pronounced stable layer between 900 and 800 mb, preventing convection and rainfall, and in the warm case (1965) the heat supply from the ocean eliminates the atmospheric stability and activates rainfall. …A side effect of the widespread warming of the tropical belt of the atmosphere shows up in the increase of exchange of angular momentum with the neighboring subtropical belt, whereby the subtropical westerly jet strengthens …The variability of the heat and moisture supply to the global atmospheric thermal engine from the equatorial Pacific can be shown to have far-reaching large-scale effects.

Klaus Wyrtki (1985), drawing on extensive observations of El Niño, writes:

A complete El Niño cycle results in a net heat discharge from the tropical Pacific toward higher latitudes. At the end of the cycle the tropical Pacific is depleted of heat, which can only be restored by the slow accumulation of warm water in the western Pacific by the normal trade winds. Consequently, the time scale of the Southern Oscillation is given by the time required for the accumulation of warm water in the western Pacific.

It is these far-reaching events that make El Niño so important. Few people care about warm water off Peru around Christmas; many care about global changes the weather. El Niño is important because of its atmospheric influence.

When the Kelvin wave reaches the coast of Ecuador, part is reflected as an westward-propagating Rossby wave, and part propagates north and south as a coastal trapped Kelvin wave carrying warm water to higher latitudes. For example, during the 1957 El Niño, the northward propagating Kelvin wave produced unusually warm water off shore of California, and it eventually reached Alaska. This warming of the west coast of North America further influences climate in North America, especially in California.

As the Kelvin wave moves along the coast, it forces Rossby waves which move west across the Pacific at a velocity that depends on the latitude \((\PageIndex{3})\). The velocity is very slow at high latitudes and fastest on the equator, where the reflected wave moves back as a deepening of the thermocline, reaching the central equatorial Pacific a year later. Similarly, the westward propagating Rossby wave launched at the start of the El Niño in the west, reflects off Asia and returns to the central equatorial Pacific as a Kelvin wave, again about a year later.

El Niño ends when the Rossby waves reflected from Asia and Ecuador meet in the central Pacific about a year after the onset of El Niño (Picaut, Masia, and du Penhoat, 1997). The waves push the warm pool at the surface toward the west. At the same time, the Rossby wave reflected from the western boundary causes the thermocline in the central Pacific to become shallower when the waves reaches the central Pacific. Then any strengthening of the trades causes upwelling of cold water in the east, which increases the east-west temperature gradient, which increases the trades, which increases the upwelling (Takayabu et al 1999). The system is then thrown into the La Niña state with strong trades, and a very cold tongue along the equator in the east.

La Niña tends to last longer than El Niño, and the cycle from La Niña to El Niño and back takes about three years. The cycle isn’t exact. El Niño comes back at intervals from 2-7 years, with an average near four years (figure \(\PageIndex{2}\)).

Equatorial Kelvin and Rossby Waves

Kelvin and Rossby waves are the ocean’s way of adjusting to changes in forcing such as westerly wind bursts. The adjustment occurs as waves of current and sea level that are influenced by gravity, Coriolis force \(f\), and the north-south variation of Coriolis force \(\partial f /\partial y = \beta\). There are many kinds of these waves with different frequencies, wavelengths, and velocities. If gravity and \(f\) are the restoring forces, the waves are called Kelvin and Poincaré waves. If \(\beta\) is the restoring force, the waves are called planetary waves. One important type of planetary wave is the Rossby wave.

Two types of waves are especially important for El Niño: internal Kelvin waves and Rossby waves. Both waves can have modes that are confined to a narrow, north-south region centered on the equator. These are equatorially trapped waves. Both exist in slightly different forms at higher latitudes.

Kelvin and Rossby wave theory is beyond the scope of this book, so I will just tell you what they are without deriving the properties of the waves. If you are curious, you can find the details in Philander (1990): Chapter 3; Pedlosky (1987): Chapter 3; and Apel (1987): §6.10–6.12. If you know little about waves, their wavelength, frequency, group and phase velocities, skip to Chapter 16 and read Section 16.1.

Figure \(\PageIndex{4}\): Sketch of the two-layer model of the equatorial ocean used to calculate planetary waves in those regions. After Philander (1990: 107).

The theory for equatorial waves is based on a two-layer model of the ocean (figure \(\PageIndex{4}\)). Because the tropical ocean has a thin, warm surface layer above a sharp thermocline, such a model is a good approximation for those regions. Equatorial-trapped Kelvin waves are non-dispersive, with group velocity: \[c_{K_{g}} = c \equiv \sqrt{g' H}, \quad \text{where} \quad g' = \frac{\rho_{2} - \rho_{1}}{\rho_{1}} g \nonumber \]

\(g'\) is reduced gravity, \(\rho_{1}\), \(\rho_{2}\) are the densities above and below the thermocline, and \(g\) is gravity. Trapped Kelvin waves propagate only to the east. Note that \(c\) is the phase and group velocity of a shallow-water, internal, gravity wave. It is the maximum velocity at which disturbances can travel along the thermocline. Typical values of the quantities in \((\PageIndex{1})\) are: \[\frac{\rho_{2} - \rho_{1}}{\rho_{1}} = 0.003; \quad H = 150 \ \text{m}; \quad c = 2.1 \ \text{m/s} \nonumber \]

At the equator, Kelvin waves propagate eastward at speeds of up to 3 m/s, and they cross the Pacific in a few months. Currents associated with the wave are everywhere eastward with north-south component (figure \(\PageIndex{5}\)).

Figure \(\PageIndex{5}\): Left: Horizontal currents associated with equatorially trapped waves generated by a bell-shaped displacement of the thermocline. Right: Displacement of the thermocline due to the waves. The figures shows that after 20 days, the initial disturbance has separated into an westward propagating Rossby wave (left) and an eastward propagating Kelvin wave (right). After Philander et al. (1984: 120).

Kelvin waves can also propagate poleward as a trapped wave along an east coast of an ocean basin. Their group velocity is also given by \((\PageIndex{2}\)), and they are confined to a coastal zone with width \(x = c/(\beta y)\).

The important Rossby waves on the equator have frequencies much less than the Coriolis frequency. They can travel only to the west. The group velocity is: \[c_{R_{g}} = - \frac{c}{(2n + 1)}; \quad n = 1,2,3, \ldots \nonumber \]

The fastest wave travels westward at a velocity near 0.8 m/s. The currents associated with the wave are almost in geostrophic balance in two counter-rotating eddies centered on the equator (figure \(\PageIndex{5}\)).

Away from the equator, low-frequency, long-wavelength Rossby waves also travel only to the west, and the currents associated with the waves are again almost in geostrophic balance. Group velocity depends strongly on latitude: \[c_{R_{g}} = -\frac{\beta g' H}{f^{2}} \nonumber \]

Wave dynamics in the equatorial regions differ markedly from wave dynamics at mid-latitudes. Baroclinic waves are much faster, and the response of the ocean to changes in wind forcing is much faster than at mid-latitudes. For planetary waves near the equator, we can speak of an equatorial wave guide.

Now, let’s return to El Niño and its “far-reaching large-scale effects.”