11.2: Dynamic Theory of Tides
- Page ID
- 4459
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Equilibrium Theory of tides predicts that each day there will be two high and two low tides, each one occurring at the same time day after day, with each pair producing tides of similar heights. While this view provides a basic explanation for the primary forces that generate the tides, it does not take into account such variables as the effects of the continents, the depth of the water, and many other factors. In all, there are almost 400 variables that must be incorporated into predicting the tides! The Dynamic Theory of tides takes these other factors into account, and shows that the tides are much more complicated and variable from place to place than the Equilibrium Theory would suggest. For example, some areas receive only one high and one low tide per day (see section 11.3). Furthermore, the tidal range varies greatly across the globe; in the Mediterranean Sea, there can be a difference of only 10 cm between high and low tides, while the Bay of Fundy in Canada experiences a tidal range of up to 17m (56 ft) every day (Figure \(\PageIndex{1}\)).

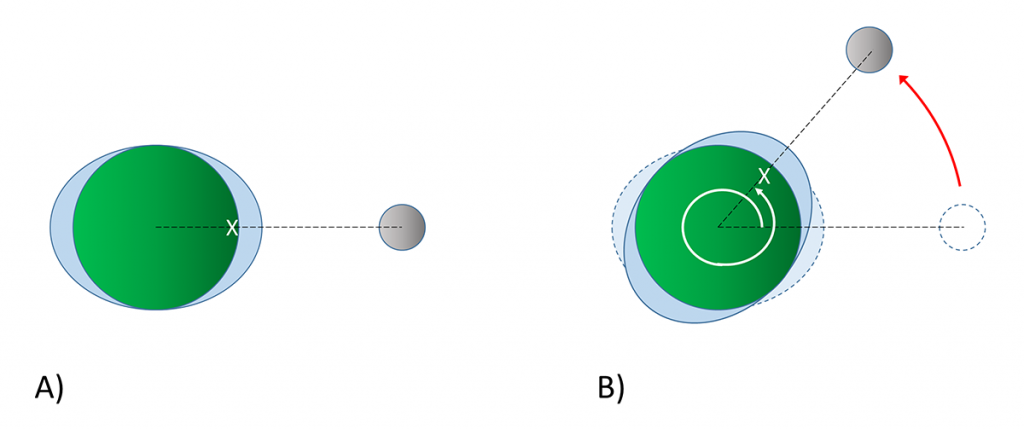
Examination of any tide chart will show that the tides don’t occur at same time each day; in fact, each tidal peak occurs about 50 minutes later than it did in the previous day. This is due to the orbit of the moon around the Earth. Imagine a high tide that occurs at a particular location (X) at 1:00 pm (Figure \(\PageIndex{2}\)). The high tide occurs as location X moves through the bulge of water facing the moon. It will take the Earth 24 hours to complete one revolution, to bring location X back to site of the water bulge that caused that high tide. However, during those 24 hours, the moon has also moved as it orbits the Earth, so the high tide bulge has moved beyond its original location. The Earth thus has to rotate an additional distance for location X to reach the bulge and experience that same high tide. Because it takes the moon about 28 days to orbit the Earth, the moon gets “ahead” of the Earth’s rotation by about 50 minutes per day. Therefore, it takes location X 24 hours and 50 minutes to rotate through the same tidal bulge, and as a result, the tidal peaks occur about 50 minutes later each day. In our example, an afternoon high tide at 1:00 pm on one day would be followed by a high tide at about 1:50 pm the following day. This 24 hour and 50 minute cycle is referred to as a tidal day.
The motion of the moon impacts the tidal cycles in other ways. As the moon orbits the Earth, its orbital plane is at an angle relative to the rotational plane of Earth. This angle, or declination, means than the moon fluctuates between an angle of 28.5o north of the equator, to 28.5o south of the equator roughly every two weeks (the cycle from maximum to minimum and back takes about 27 days). Figure \(\PageIndex{3}\) illustrates a case where the moon is at its maximum declination 28.5o north of the equator, creating its corresponding tidal maxima. A point on the Earth at the latitude indicated by the red line would experience two high tides as it rotated through 24 hours, at points A and B. But the two high tides would not be of equal heights; the high tide at A would be higher than the high tide at B. This helps create a mixed semi-diurnal tide; two high tides of different heights per day (see section 11.3).

Finally, the continents and the bottom topography of the oceans have an impact on the tides that are experienced in an area. Because the tides are essentially waves with extremely long wavelengths extending halfway across the Earth, they behave as shallow water waves, and they are influenced and refracted by the bottom contours, leading to regional tidal variations. When the tidal crests encounter land, they are are reflected, and the wave moves back out to sea, theoretically until it encounters another continent on the opposite side of the ocean basin. The crest is once again reflected, and the water oscillates back and forth as a standing wave across the ocean basin. However, because of the scale over which these tidal waves move, we must take into account the influence of the Coriolis Effect. As the tidal crest is reflected back across the ocean basin, its path is deflected by the Coriolis force; to the right in the Northern Hemisphere, and to the left in the Southern Hemisphere (see section 9.1). Using the Northern Hemisphere as an example, imagine a tidal crest that has reached land on the western side of an ocean basin. It would have a tendency to be reflected and move across the basin towards the east. But the Coriolis force deflects the movement to the right, causing the crest to instead head south. When the crest hits land in the south, it would now tend to reflect towards the north, but once again the Coriolis deflection to the right kicks in, and the wave instead moves to the east. From the east the reflected wave is deflected to the north, and so on. The result of all of this is that instead of a simple standing wave moving back and forth across the ocean, the tidal crest follows a circular pattern around the ocean basin, counterclockwise in the Northern Hemisphere and clockwise in the Southern Hemisphere. This is analogous to shaking a pan full of water in a circular manner, and watching the water follow a similar circular path as it sloshes around inside. This large scale circular rotation pattern of tides is called amphidromic circulation (Figure \(\PageIndex{4}\)). The rotation occurs around a central amphidromic point or node, that shows little tidal variation, while the largest tidal ranges occur on the edges of the circulation pattern. In Figure \(\PageIndex{4}\) the amphidromic points are indicated by the dark blue areas where the white lines converge, like spokes from a bicycle wheel, and the dark red and brown areas show the regions of maximum tidal heights. The tidal maxima will rotate around the amphidromic points, taking about 12 hours for a complete rotation, leading to two high and two low tides per day in many places. If a tidal maximum is occurring along one of the white lines in Figure \(\PageIndex{4}\) at a certain time in the Northern Hemisphere, one hour later that high tide will have moved to the white line to the left (counterclockwise), and so on until it completes a rotation. In the Southern Hemisphere, the tide will move to the line to the right for clockwise rotation.

The result of all of these variables is that the tides will not always occur twice each day, at the same time and with equal heights as the Equilibrium Theory of tides may suggest. Instead, each region of the oceans has a unique set of factors that contribute to the types of tides it will experience. The major types of tides are discussed in the next section.


