6.4: Sound

Sound is a form of energy transmitted through pressure waves; longitudinal or compressional waves similar to the seismic P-waves we discussed in section 3.3. With ocean sounds, the energy is transmitted via water molecules vibrating back and forth parallel to the direction of the sound wave, and passing on the energy to adjacent molecules. Therefore, sound travels faster and more efficiently when the molecules are closer together and are better able to transfer their energy to neighboring particles. In other words, sound travels faster through denser materials. Since water is much denser than air, the speed of sound in water (about 1500 m/s) is approximately five times faster than the speed in air (around 330 m/s). This helps explain why we sometimes have difficulty localizing the source of a sound that we hear underwater. We localize sound sources when our brains detect the tiny differences in the time of arrival of sounds reaching our ears. A sound coming from our left will reach our left ear a fraction of a second before reaching our right ear. Our brains can process that small difference in time of arrival to recognize the direction from which the sound came. In water, the sound is so much faster that the difference in arrival time between our ears becomes too small for us to interpret, and we lose the ability to localize the source.

However, as with sound in air, the speed of sound in the ocean is not constant; it is influenced by a number of variables including temperature, salinity, and pressure, and an increase in any of these factors will lead to an increase in the speed of sound. We have seen that these variables change with depth and location; so to will the speed of sound differ in different regions of the ocean.

To examine the way the speed of sound changes as a function of depth, we need to consider the vertical profiles for temperature and pressure. At the surface, the pressure is low, but the temperature is at its highest point in the water column. The temperature effects dominate at the surface, so the speed of sound is fast in surface waters. As depth increases, the temperature and the speed of sound decline. Near the bottom, the extreme pressure dominates, and even though temperatures are low, the speed of sound increases with depth. At moderate depths (between a few hundred and one thousand meters) there is a zone where both temperature and pressure are relatively low, so the speed of sound is at a minimum. This zone of minimum speed is called the SOFAR channel (Sound Fixing And Ranging) or the Deep Sound Channel (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\) Profiles of temperature, pressure, and sound speed with depth. Sound speed is high at the surface due to the high temperatures, and is high at depth because of the high pressure. At moderate depths lies the SOFAR channel, the region of slowest sound speed (PW).

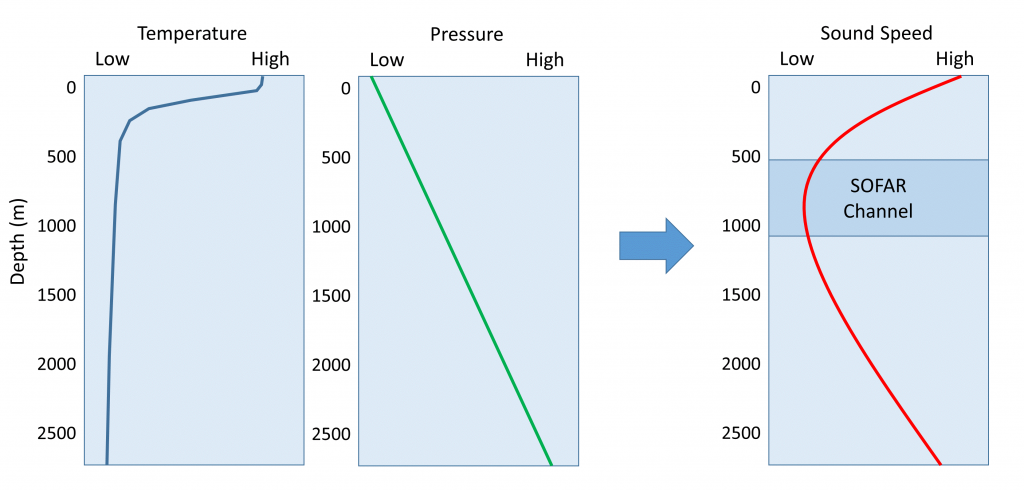
The SOFAR channel is important because sounds produced in that region can be propagated over very long distances with little attenuation (loss of energy). Sound waves produced in the channel radiate out in all directions. Waves that travel into shallower or deeper water outside of the sound channel are entering a region of faster sound transmission. As we saw with seismic waves, when these sound waves encounter a region of differing transmission speed, the waves tend to be refracted or bent back towards the region of lower speed. As a result, sound waves moving from the SOFAR channel into shallower water will be refracted back towards the channel. As the sound waves go deeper below the channel, they will be refracted upwards, back into the channel and the region of slower speed. In this way, much of the sound does not dissipate out into the water in all directions, but instead is trapped within the channel, and can travel very long distances with little loss of energy (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\) Sound propagation in the SOFAR channel. Sound waves emanating from a source will be refracted towards the region of slower speed, “trapping” the sound in the SOFAR channel (PW).

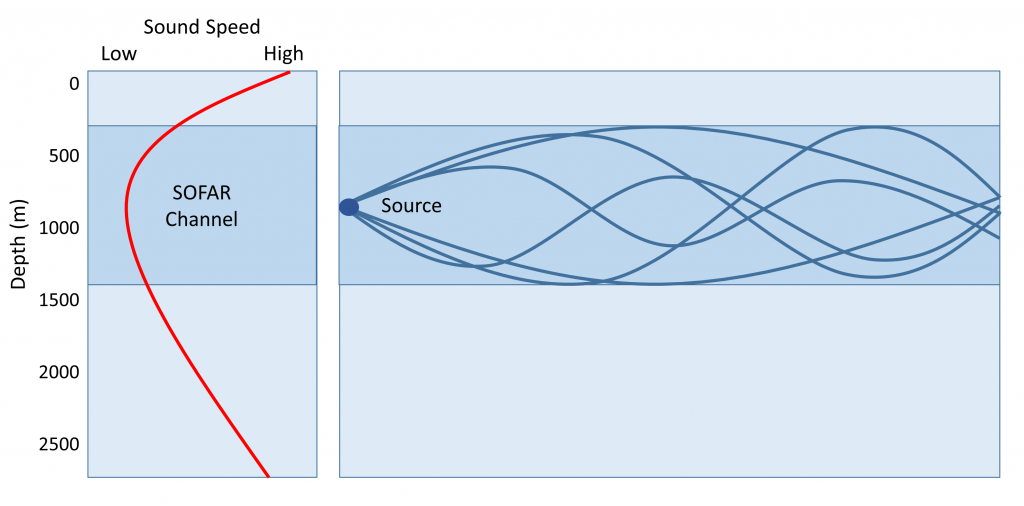
There are several practical applications of the SOFAR channel. Baleen whales are thought to use the SOFAR channel to communicate with each other over long distances of hundreds to thousands of kilometers. Their vocalizations are very loud and are low frequency calls, which travel farther than high frequency sounds in the oceans. The military has been able to track submarines using the SOFAR channel, and during World War II it was used to locate downed pilots or missing ships and planes. A stranded pilot could drop a small device into the water, and once it sank into the SOFAR channel it would explode, creating a sound that could be heard at multiple listening stations. Using the time of arrival of the sound at the various receivers, the location of the source could be determined through triangulation. In the 1990s it was suggested that the SOFAR channel could be used to monitor global ocean temperatures. A project known as ATOC (Acoustic Thermometry of Ocean Climate) was proposed where loud, low frequency sounds produced near Hawaii and California would travel through the SOFAR channel to receiving stations around the Pacific. By monitoring the time it took for the sounds to reach the receivers, scientists could monitor changes in ocean temperatures on a global scale, as sounds would move faster through a warming ocean.

Since sound travels better through water than air, the energy required to transmit a given sound wave is higher in air than in water. The energy, or intensity (loudness) of a sound is measured on the decibel (dB) scale. It turns out that it takes about 61 times more energy to transmit a sound through air than through water. Because of this energy difference, there is a 61 dB difference between sounds transmitted through air and water, such that a sound intensity of 120 dB in water would be equivalent to an intensity of about 60 dB in air. This should be kept in mind when trying to compare sounds in the ocean with sounds in the air. A sound of 130 dB in air is about equivalent to standing 100 m from a jet engine at takeoff. A sound of 130 dB in water is equivalent to about 70 dB in air, which is the intensity of the sound of a vacuum cleaner. It should also be pointed out that on the dB scale, an increase of 10 dB means the sound is 10 times louder. In other words, 20 dB is 10 x louder than 10 dB, while 30 dB is 100 x louder than 10 dB.

---

Additional links for more information:

• Discovery of Sound in the Sea website: http://www.dosits.org/