4.2: Overview, Solar Energy, Pressure, and Wind Belts
- Page ID
- 14941
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The connections between atmospheric circulation, ocean currents and Earth's climate are both simple and wonderfully complex. We could easily spend the whole semester studying these topics and developing the background for ocean circulation, but we won't. Instead, we'll hit the high points and build a background for understanding ocean currents and thermo-haline circulation. It makes sense to start with atmospheric circulation because ocean surface currents are driven by wind. The basic pattern of surface ocean circulation, including the large-scale gyres, is caused by wind and the factors that produce large-scale wind patterns. We need to start by seeing how solar energy input on Earth and poleward transport of heat by winds sets up large-scale atmospheric cells that produce Easterly and Westerly winds in three main bands from the equator to the poles. The Coriolis effect, produced by Earth's rotation and conservation of momentum, plays an important role here. Ocean structure also plays an important role and we need to look at density driven circulation in the ocean as produced by temperature and salinity: so-called thermohaline circulation. Ocean circulation is three-dimensional and both surface currents and deep water currents play an important role in heat transport. Large-scale ocean currents are impacted by the Coriolis effect, and depth-variations in coupling between surface flow and wind stress produce another important effect, known as Ekman transport, which we will discuss. Ultimately, when we put all the pieces together, the goal is to arrive at a coherent picture of how solar energy, winds, and ocean circulation combine to produce a global thermostat for Earth.
It's all about Blowing Hot Air
This image shows large-scale atmospheric circulation on Earth. Note the three-dimensionality of the circulation. On the right-hand side of the image the arrows show vertical and horizontal air flow as part of six convection cells, three in each of the Northern and Southern hemispheres. The central part of the image shows surface winds blowing from the east (the Trade winds) or the west (The Westerlies) --note that the Polar Easterlies are not easily seen in this image.
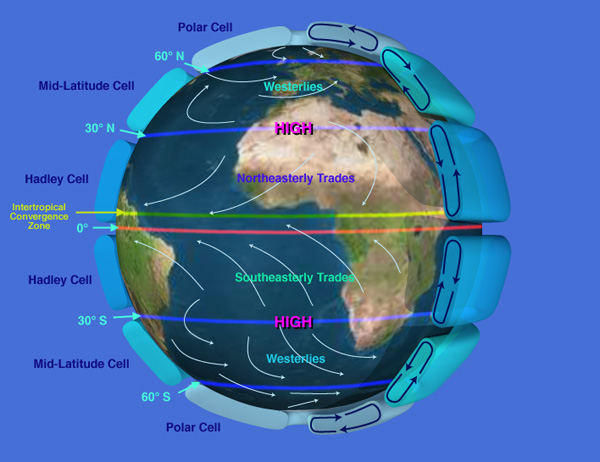
Atmospheric Circulation and the Trade Winds
Source: NASA
Hadley circulation
One of the most important things to understand from this image is that everything is driven by unequal solar heating as a function of latitude. The energy from our Sun is focused on the equatorial region and spread comparatively thinly over the polar regions. This is true on an average annual basis, Earth receives more solar energy at the equator than at the poles. As a result, the land, water, and air, over the equator are warm, and air rises over the equator. This warm air rises through the atmosphere and flows poleward as an upper atmosphere wind that is, essentially, an air-mail package of heat known as a Hadley Cell. The image here has arrows showing circulation in a vertical plane along a line of longitude (just to the east of the African continent) but, of course, this circulation occurs at all longitudes. Hadley circulation is 3D; heat moves poleward in upper atmosphere winds and there is a return flow from north to south (in the Northern hemisphere) that sets up the Northeasterly Trade winds (with the help of the Coriolis effect, as we'll see below).
Pressure belts
The Hadley Cell is set up by rising air over the equator. It begins with warming of air surrounding the equator, which creates a large region of lower surface pressures (due in part to the fact that columns of warm air weigh less than columns of cold air). This belt of equatorial low pressure causes air to be drawn together in a region called the Intertropical Convergence Zone (ITCZ). The convergence of warm, moist air over the equator transports large volumes of air aloft, to the top of the troposphere. This air is confined vertically by the base of the stratosphere and thus spreads out north and south toward the poles.
Because of Earth's spherical shape, the poleward-flowing air is compressed into an increasingly smaller volume as it moves away from the equatorial region. The airmasses also cool as they move poleward. The buildup of cool air aloft causes surface pressures to rise because surface pressure depends on the weight of the entire atmospheric column. The mass convergence and cooling also cause air mass densification, which forces some of the air aloft to sink. At some point, normally ~ 30 deg. North/South, the increase in surface pressures reaches a maximum, marking a belt of subtropical high pressure. Sinking air is dry and characterized by a lack of clouds and precipitation. These regions of subtropical high pressure systems are known for their tranquil weather. Air masses flowing equatorward from these high pressure belts form the Trade Winds that feed the ITCZ, thus completing the Hadley Cell circulation. Similar thinking explains the existence and wind circulation in the Ferrel Cell (labeled the 'mid-latitude' cell in this image) and the Polar Cell.
Activity 1: Pressure Belts
Let's think about the global pattern of atmospheric pressure. Hadley circulation implies a systematic pattern of pressure variation as a function of latitute. One question we could ask involves differences in air masses within a Hadley cell. Referring to the figure above: how do air masses differ between the ascending limbs of a Hadley Cell, over the equator, compared to the descending limb at 30 deg. North?
- Atmospheric Pressure(link is external) Start by skimming this page. Look at Figures 7d-1 and 7d-4 and read the associated text. (Note: The animation for 7d-4 may open in a separate Quicktime window or be downloaded to your desktop)
- Using these data, let's calculate the average density for air at 30 deg. North compared to that at the equator. You can assume that the atmosphere extends to the 70 km, which is within the Mesosphere. A useful formula for the relationship between pressure, p, density, ρ, gravity, g, and height, h, is: p = ρgh
- Let's assume that the average air pressure over the equator at Earth's surface is roughly 101.3 kPa (recall: 1 Pa = 1 Newton per square-meter). Does this jive with what you see in figure 7d-4? In this case, what is the average density of air if the column is 70 km tall?
- Now calculate the density at 30 deg. north, assuming an average surface pressure of 102.5 kPa.
- Comment on how air pressure varies as a function of time throughout the year (hint, look at the animation on the web page that you just read).
- Thinking back to what you know about heat capacity and latent heat, do these differences in density make sense relative to your expectations for heat transfer by large-scale winds? Is the air at 30 deg. north likely to be colder/warmer/denser compared to that at the equator?
Submitting your work
Save your document as either a Microsoft Word or PDF file in the following format:
L4_Activity1_AccessAccountID_LastName.doc (or .pages or .pdf)
For example, student Elvis Aaron Presley's file would be named "L4_Activity1_eap1_presley.doc".
Put the file in the DropBox under Lesson 4 on Canvas.
Grading Criteria
See the grading rubric for specifics on how this assignment will be graded.


