3.2: Ice, Water, and Vapor
- Page ID
- 14929
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
We will first examine water as a molecule, and then explore the implications of water's molecular structure for its physical behavior and its importance as a "universal solvent." This first section examines the phases of water.
Reading assignment
Read Chapter 6 (pp. 151-182) in Life's Matrix: A Biography of Water by Philip Ball(link is external), then read the material in this section. Ball, an editor for Nature, has an elegant way of framing the "weirdness" of the water molecule that highlights water's unusual properties. This chapter is a nice treatment to accompany our "drier" outline below.
The Water Molecule
A molecule of water is composed of two atoms of hydrogen and one atom of oxygen. Now, the one and only electron ring around each hydrogen atom has only one electron. The negative charge of the electron is balanced by the positive charge of the one proton in the nucleus. Protons have mass, electrons do not. One electron and one proton: hydrogen has an atomic number of one. In the hydrogen nucleus is also one neutron; no charge but the weight of one proton. One proton, one neutron: hydrogen has an atomic weight of two. The electron ring of hydrogen would like to possess two electrons to create a stable configuration. Oxygen, on the other hand, has an inner electron ring with two electrons, which is cool because that is a stable configuration. The outer ring, on the other hand, has six electrons but it would like to have two more because in the second electron ring, eight electrons make the stable configuration. To balance the negative charge of eight (2+6) electrons, the oxygen nucleus has eight protons. Eight protons and eight electrons: oxygen has an atomic number of eight. The eight protons in the nucleus are matched by eight neutrons. Eight protons, eight neutrons: oxygen has an atomic weight of 16. Hydrogen and oxygen would like to have stable electron configurations but do not as individual atoms. They can get out of this predicament if they agree to share electrons (a sort of an energy "treaty"?). So, oxygen shares one of its outer electrons with each of two hydrogen atoms, and each hydrogen atom shares its one and only electron with oxygen. This is called a covalent bond. Each hydrogen atom thinks it has two electrons, and the oxygen atom thinks that it has eight outer electrons. Everybody's happy, no?
Figure. 1:
O
/ \
H H
However, the two hydrogen atoms are both on the same side of the oxygen atom with an angle of about 105 degrees between them (see Fig. 1) so that the positively charged nuclei of the hydrogen atoms are left slightly exposed, so to speak, leaving that end of the water molecule with a weak positive charge. Meanwhile on the other side of the molecule, the electrons of the oxygen atom give that end of the molecule a weak negative change. For this reason, a water molecule is called a "dipolar" molecule. Water is an example of a polar solvent, capable of dissolving most other compounds. In solution, the weak positively charged side of one water molecule will be attracted to the weak negatively charged side of another water molecule and the two molecules will be held together by a weak "hydrogen bond," and so on. At the temperature range of seawater, the weak hydrogen bonds are constantly being broken and re-formed. This gives water some structure, but allows the molecules to slide over each other easily, making it a liquid.
Water Properties
A calorie is the amount of heat it takes to raise the temperature of 1 g of pure water 1 degree C at sea level. Therefore, it would take 100 calories to heat water from 0˚, the freezing point of water, to 100˚C, the boiling point. However, it would take 540 calories to convert that 1 g of water at 100˚C to 1 g of water vapor still at 100˚C. This is called the heat of vaporization. You would have to remove 80 calories from 1 g of water at the freezing point, 0˚C, to convert it to 1 g of ice at 0˚ C. This is called the heat of fusion.
Water does not give up or take up heat very easily. Therefore, it is said to have a high heat capacity. In Pennsylvania, it is common to have a difference of 20˚C between day and night temperatures. During the same time frame, the temperature of lake water would hardly change at all.
Water flows easily. It is said to have a low "viscosity." Compare this with motor oil or honey that each have relatively high viscosities (or to the upper mantle that has an even higher viscosity as discussed in class during our "plate tectonics" lectures). If you can't get the honey to flow out of the jar and onto your toast in the morning, you put it in the microwave and "nuke" it, then it flows easily, i.e. increasing the temperature lowers the viscosity. Similarly, warm water is less viscous than cold water.
Pure water has a density of 1.0 g/cm3 at 4˚C. As you increase or decrease the temperature from 4˚C, the density decreases. In fact, if you measure the temperature of the deep water in large, temperate-latitude lakes that freeze over in the winter, you will find that the temperature is 4˚C; that is because fresh water is at its maximum density at that temperature, and as surface waters cool off in the fall and early winter, the lakes overturn and fill up with 4˚C water. As you add dissolved solids to pure water to increase the salinity, the density increases. The density of average seawater with a salinity of 35 o/oo (35 g/kg) and at 4˚C is 1.028 g/cm3 As you add salts to seawater, you also change some other properties. Increasing salinity increases the boiling point and decreases the freezing point. Normal seawater freezes at -2˚C, 2˚C colder than pure water. Increasing salinity also lowers the temperature of maximum density.
When Water Freezes, It Expands

Fig. 2 A rough sketch of water molecules in ice crystal (hexagonal form)
When water is a liquid, the water molecules are packed relatively close together, but can slide past each other and move around freely (that makes it a liquid). When water freezes, however, bonds are formed that lock the molecules in place in a regular (hexagonal) pattern (Fig. 2). For nearly every known chemical compound, the molecules are held closer together (bonded) in the solid state (e.g., in mineral form or ice) than in the liquid state. Water, however, is unique in that it bonds in such a way that the molecules are held farther apart in the solid form (ice) than in the liquid form. Water expands when it freezes making it less dense than the water from which it freezes. In fact, its volume is a little over 9% greater (or density ca. 9% lower) than in the liquid state. For this reason, ice floats on the water (like an ice cube in a glass of water). This latter property is very important for organisms in the oceans and fresh-water lakes. For example, fish in a pond survive the winter because ice forms on top of the pond (it floats) and effectively insulates (does not conduct heat from the pond to the atmosphere as efficiently) the rest of the pond below, preventing it from freezing from top to bottom (or bottom to top). If water did not expand when freezing, then it would be denser than liquid water when it froze; therefore, it would sink and fill lakes or the ocean from bottom to top. Once the oceans filled with ice, life there would be impossible. We are all aware that the expansion of liquid water to ice exerts a tremendous force. If you have ever put a full container of water with a tight-fitting lid, or a can of soda in the freezer, you may have experienced this. Ten cups of water will to turn into 11 cups of ice when it freezes. The force of the crystallization of ice is capable of bursting water pipes and causing cracks in rocks to expand, thus accelerating the erosion of mountains!
The diagram below (Fig. 3) illustrates some changes in the freezing point and the density of pure water, and changes imposed by salt addition. Note that the density of pure water is at a maximum at 4°C, whereas density continues to increase as temperature decreases when the salt content is 35 o/oo (parts per thousand)--near the average salinity of seawater. Also, the freezing point of water is depressed when salt is added (that's why we put salt on icy roads and sidewalks!). We will explore the implications of this later in the course when we consider the circulation of the oceans and the production of "deep" water. Water is only slightly compressible as demonstrated by the small, but measurable, change in density as pressure increases. Pressure is measured here in bars (not the kind you might be savoring about now), where 1 atmosphere (the pressure at sea level) equals = 1.01325 bar = 101.3 kPa. Thus, the maximum pressure of 4000 bars on the graph is equivalent to the pressure at about 4000 meters depth in the ocean (the average depth of the ocean is about 3800 meters). Pressure increases at the rate of one atmosphere every 10 meters (those of you who dive know this). Air-filled volumes, such as human body cavities, cannot withstand the water pressures at depth (this includes most things except for the specially strengthened hulls of submersibles and submarines), but if we could fill our lungs with water and somehow still respire, like fish, we could do some interesting diving. Even at 4000 meters, water has compressed only about 2.3% with respect to the volume it had at the surface (an increase in density of 2.3%, do the calculation given the graphical data below). What was the name of the movie that used that principle? OK, on to the next section...
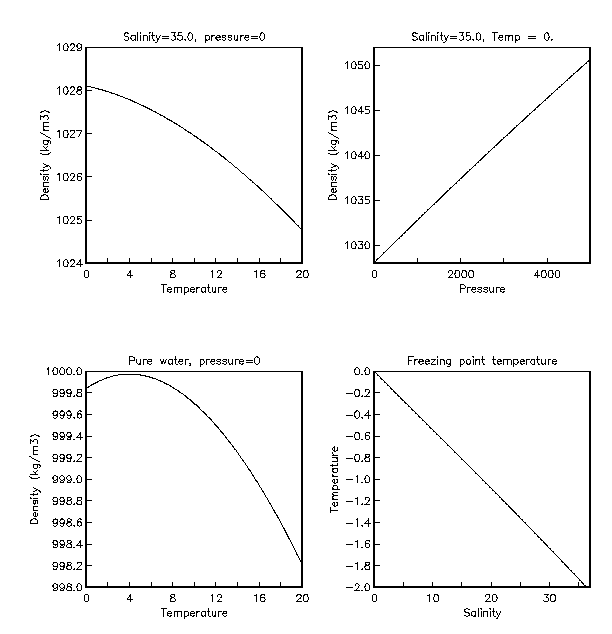
Figure 3: The change in seawater density at 35 o/oo with pressure (bars) (top), and density and freezing points of pure water and saltwater (bottom).
Credit: ucsd.edu


