10.1: What does turbulent drag do to horizontal boundary layer flow?
- Page ID
- 6552
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The turbulent drag force on the horizontal air flow within the atmospheric boundary layer can approach the size of the other terms in the horizontal equation of motion. Note that this turbulent drag force acts to reduce the air velocity and therefore is opposite the air flow velocity vector.
Let’s look at the force balance when the turbulent drag force is included. We will call this turbulent drag "friction" because it is commonly called that, but it is really quite different.
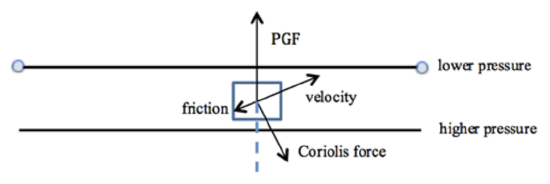
Credit: W. Brune
Note that the turbulent drag (friction) force is parallel to the velocity vector and is opposite in direction.
In the x-direction (along the isobars) the balance of forces is:
friction (x-component) = Coriolis (x-component).
In the y-direction (perpendicular to the isobars), the balance of opposing forces is:
friction (y-component) + Coriolis (y-component) = PGF
Because of the turbulent drag force and the velocity dependence of the Coriolis force, the parcel velocity points toward the lower pressure and the air parcel will tend to move across isobars toward the low pressure. Typical cross-isobaric flow in the boundary layer makes an angle of \(30^{\circ}\) with the isobars. Thus, surface air moves toward low pressure and away from high pressure.
Above the atmospheric boundary layer, however, turbulent drag is not generally important and geostrophic and gradient flows are good approximations.
The effects of turbulent drag are very important for weather. When divergence aloft causes upward-moving air below, it becomes associated with a low-pressure region near Earth's surface. A pressure gradient force is created, but the air moving toward the low pressure is turned to travel counterclockwise around the low by the Coriolis force. However, turbulent drag slows the wind and turns it to cross isobars toward the low pressure, creating convergence, which causes uplift, clouds, and perhaps precipitation. The opposite is true for surface high-pressure regions occurring under regions of convergence aloft, which causes descent. The anticyclonic winds around the surface high are slowed and turn outward, causing divergence near the surface, leading to descending air and clear skies. The following video (1:43) provides further discussion of friction:
Friction
- Click here for transcript of the Friction video.
-
When the flow is in the upper part of the atmospheric boundary layer, which is a kilometer or two above the surface, the turbulence in the boundary layer acts to impede the horizontal wind. This resistance to flow is not really friction. But it does act to slow the wind down, no matter the wind's direction. As a result, we can assume that this turbulent drag is a force that opposes the wind velocity. Look at what adding a turbulent resistant turn does to the force balance for straight line flow in the upper boundary layer. The PGF force is perpendicular to the pressure gradient as usual. However, the friction opposes the velocity, and slows it down. At the same time, the Coriolis force is always perpendicular to the velocity and to the right. And because the velocity is slowed down, the Coriolis force is less. The velocity vector gets turned toward the PGF vector, and thus toward the low pressure. Note that the x direction of the frictional force must balance and be opposite to the x direction of the Coriolis force. And the y directions of the friction and Coriolis forces must be opposite to and balance the PGF in the y direction in the diagram. Boundary layer turbulent drag turns to velocity across isobars for low pressure, which causes convergence, while boundary layer turbulent drag turns to velocity across isobars away from high pressure, which causes divergence. These friction effects tend to amplify the convergence into surface low pressure and divergence from surface high pressure.
Quiz 10-3: Balance of forces and motion.
- Find Practice Quiz 10-3 in Canvas. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
- When you feel you are ready, take Quiz 10-3. You will be allowed to take this quiz only once. Good luck!

