5.2.2: The Velocity of Light in Crystals and the Refractive Index
- Page ID
- 18974
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When light passes near an atom, perhaps in a crystal, the vibrating electric wave causes electrons orbiting the atom to oscillate. The oscillations absorb energy from the light, and the wave slows. As light passes from air into most nonopaque minerals, its velocity may decrease by a third or a half. Because the frequency of the light remains unchanged, we know that the wavelength must decrease by a similar fraction (because v = λν).
A wave’s velocity through a crystal is described by the crystal’s refractive index (n), which depends on chemical composition, crystal structure, and bond type in the crystal. The refractive index (n) is the ratio of the velocity (v) of light in a vacuum to the velocity in the crystal:
blankn = vvacuum / vcrystal
Because light passes through a vacuum faster than through any other medium, n always has a value greater than 1. High values of n correspond to materials that transmit light slowly. Under normal conditions, the refractive index of air is 1.00029. Because it is much easier to work with air than with a vacuum, this is a common reference value and we often calculate refractive index as:
blankn = vair / vcrystal
| Refractive Index Values | |
| air fresh water fluorite borax sodalite window glass quartz garnet zircon zincite diamond |
1.000293 1.333 1.434 1.466 1.480 1.52 1.533 1.78 1.923 2.021 2.419 |
Most minerals have refractive indices between 1.5 and 2.0 (see examples in the table to the right). Fluorite, borax, and sodalite are examples of minerals that have a very low ( < 1.5) index of refraction. At the other extreme, zincite, diamond, and rutile have very high indices (> 2.0). The refractive index is one of the most useful properties for identifying minerals in grain mounts but is less valuable when we examine thin sections because it is impossible to determine precise values for n when viewing minerals in thin section.
5.2.2.1 Snell’s Law and Light Refraction
We have all seen objects that appear to bend as they pass from air into water. A straw in a glass of soda, or an oar in lake water, seem bent or displaced when we know they are not. We call this phenomenon refraction. Figure 5.10 shows an example – a pencil in a glass of water. Refraction occurs when light rays pass from one medium to another (for example water and air in Figure 5.10) with a different refractive index. If the light strikes the interface at an angle other than 90°, it changes direction and can distort a view. (Refraction occurs for waves of many different types, not just light waves. For example, earthquake waves are refracted as they interact with layers in Earth.)

When refraction occurs, a light beam bends toward the medium with higher refractive index (where light travels slower) because one side of the beam moves faster than the other. Consider a beam traveling from air into water (Figure 5.11a). The side of the beam that reaches the interface first will be slowed as it enters the water. It sort of stubs its toe. So the beam bends toward the water. However, no refraction occurs for beams traveling at 90° to an interface between media with different refractive indices; the beam follows a straight course.

Figures 5.11b shows the opposite case: a beam traveling from a medium with a high refractive index (slower light velocity) into another with a lower refractive index (faster light velocity). The beam refracts toward the medium with a higher index, as it did in Figure 5.11a.
As seen in Figure 5.11, when light reaches an interface between two different media, the angle between the beam and a perpendicular to the interface is the angle of incidence (θi). After crossing the interface, the angle between the beam and a perpendicular to the interface is the angle of refraction (θr). The relationship between the angle of incidence (θi) and the angle of refraction (θr) is
\[\dfrac{\sin(θ_i)}{\sin(θ_r)} = \dfrac{v_i}{v_r} = \dfrac{n_r}{n_i}\nonumber\]
where vi and vr are the velocities of light through two media, and ni and nr are the indices of refraction of the two media. This relationship, Snell’s Law, is named after Willebrod Snell, the Dutch scientist who first derived it in 1621.
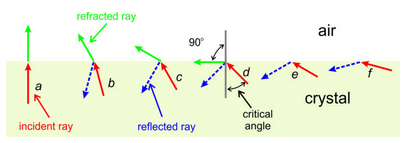
Figure 5.12 shows an incident light ray passing from within a crystal to air outside the crystal. If the incident ray is perpendicular to the crystal-air interface (drawing a), all light leaves the crystal. If the angle incidence is small (drawing b), most light escapes and is refracted at some angle to the crystal face, but some light reflects back into the crystal. We call this internal reflection. As the angle of incidence increases, the proportion of light that is reflected increases. When the angle of incidence becomes large enough (drawing d), the refracted ray travels along the crystal-air interface. And for greater incidence angles, no refraction can occur and all light reflects back into the crystal.
Rearranging Snell’s Law tells us that we can calculate the angle of refraction as follows:
blankθr = sin-1[(ni/nr) x sin θi]
By definition, sine values can never be greater than 1.0. Suppose a light beam is traveling from a crystal into air. In this situation, ni > nr, and because the term in square brackets on the right-hand side of the equation above must be less than or equal to 1.0, for some large values of θi there is no solution. The limiting value of θi is the critical angle of refraction (Figure 5.12d). If the angle of incidence is greater, none of the light will escape; the entire beam will be reflected inside the crystal as shown in Figures 5.12 e and f. This is the reason crystals with a high refractive index, such as diamond, exhibit internal reflection that gives them a sparkling appearance. Measuring the critical angle of refraction is a common method for determining refractive index of a mineral. Instruments called refractometers enable such measurements.
In Figure 5.12d, the critical angle (θi) is about 45o. The angle of refraction (θr) is 90o. Plugging these values into Snell’s law (above) we find that vi/vr is 0.7071. In other words, the velocity of light through the crystal is 71% of the velocity through air and, inverting this we find that the crystal has a refractive index of about 1.41. This is on par with many minerals that have low refractive indices.
5.2.2.2 Dispersion and Luster

The refractive index of most materials varies with the wavelength of light. In other words, the velocity of light in a crystal varies with the light’s color. This variation is dispersion. One consequence of dispersion is that different colors of light follow different paths through a crystal because they refract at different angles (according to Snell’s Law). We can sometimes see dispersion in thin sections but it is only readily apparent in a few minerals. An excellent but nonmineralogical example of dispersion is the separation of white light into different colors when refracted by a glass prism (Figure 5.13). When a beam of white light enters and exits a prism, different wavelengths (colors) exit at different angles, resulting in the production of colorful rainbows. Note also the reflected beam of white light in Figure 5.13. Reflection and refraction often occur together; their relative intensities depend on the angle at which the light hits an interface.

For a mineralogical example of dispersion, we may consider diamond. Diamond’s extreme dispersion accounts, along with its high refractive index, for the play of colors (fire) that diamonds display (seen in Figure 5.14). If not for dispersion, diamonds might sparkle, but the sparkles would all be the same color. Minerals with low dispersion generally appear dull no matter how well cut or faceted. They may, however, be useful as lenses because dispersion can separate colors and cause unwanted effects.
A mineral’s refractive index and dispersion profoundly affect its luster. Minerals with both very high refractive index and dispersion, such as diamond or cuprite, appear to sparkle and are termed adamantine. Minerals with a moderate refractive index, such as spinel and garnet (n = 1.5 -1.8), may appear vitreous (glassy) or shiny; those with a low refractive index, such as borax, will appear drab because they do not reflect or refract as much incident light. Refractive index depends on many things, but a high n-value suggests minerals composed of atoms with high atomic numbers, or of atoms packed closely together.


