1.8: Fabrics
- Page ID
- 12514
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction: foliations and lineations
Any rock that has properties that vary with direction is said to have fabric. Like most structures, fabrics can be primary or secondary. Examples of primary fabric are bedding in sedimentary rocks and flow banding in igneous rocks. Secondary fabrics typically indicate that strain has occurred. Fabrics are common in folded rocks, and if fabrics develop at the same time as folding they often have a very specific relationship to folds.
Fabrics may be planar or linear. Planar fabrics are also called foliations. (Note that some textbooks restrict the term foliation to particular types of planar fabric, with coarse mineral grains as in a schist; we will use it in a more general sense to designate any planar fabric.) Rocks with a strong secondary planar fabric are sometimes called S-tectonites (the S is for schistosity). Linear fabrics are called lineations. Rocks with a strong secondary lineation are sometimes called L-tectonites.
It is common to find a lineation that lies parallel to (or in the plane of) a planar fabric. Rocks with a strong tectonic lineation that lies in the plane of a tectonic foliation are sometimes called LS-tectonites.
Fabric Elements
Fundamental to the description of fabrics is the concept of a fabric element. Fabric elements (Fig. 1, 2) are the things that are aligned to give a rock a fabric. Fabric elements include things like layers and lenses of different composition, grains of minerals that are tabular (like mica) or acicular (like hornblende or sillimanite). Folds can also be fabric elements, if there are enough of them.
This leads to a second important concept: the idea of a penetrative fabric. A fabric is penetrative if it is present everywhere in the rock. For example, some slates can be split almost anywhere: there’s effectively an infinite number of cleavage planes. In others, the cleavage planes are visibly spaced and are termed non-penetrative.
Penetrative fabrics
A fabric is penetrative if:
- It is present throughout the rock;
- It is not possible to count the number of fabric planes or lines;
- It is not possible to see spaces between the fabric planes or lines.
Non-penetrative fabrics
A fabric is non-penetrative if:
- The fabric planes or lines are spaced apart within the rock, or
- It is possible to see spaces between the fabric planes or lines where no fabric is present, or
- The fabric planes or lines can be counted.
Note that penetrative character is a scale-dependent concept; a fabric that is penetrative at map and outcrop scale may prove to be non-penetrative in thin section.
Fabric elements
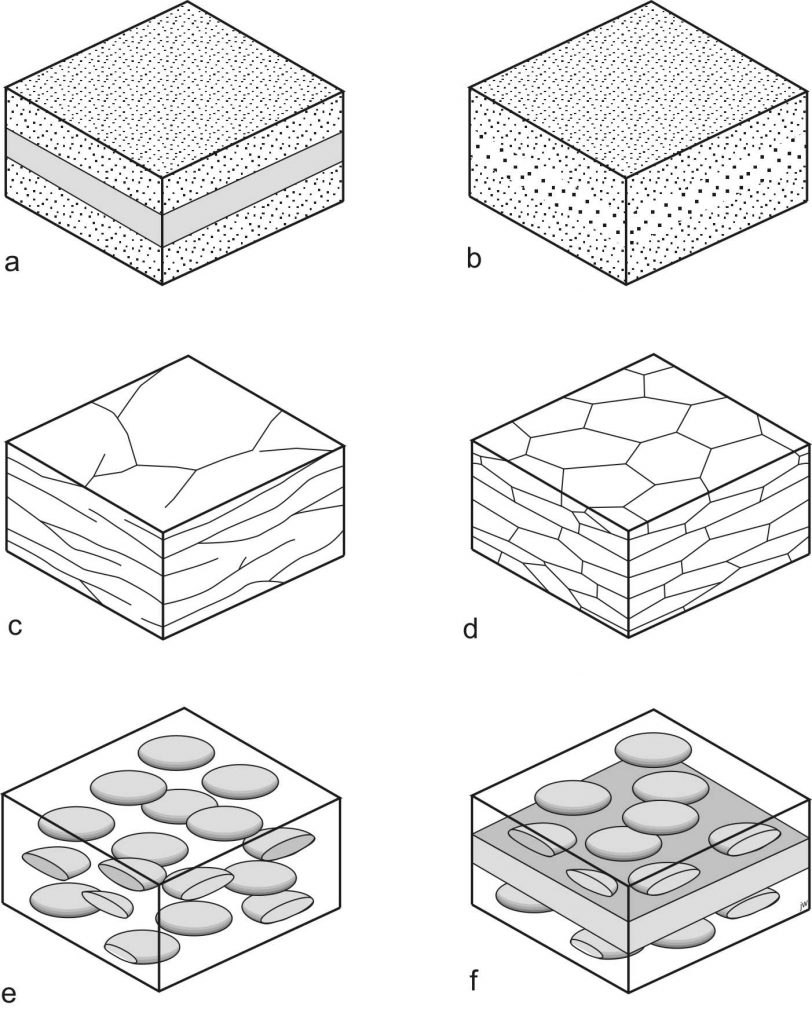
The following types of fabric elements can give a rock a fabric. Notice that it’s common for a given fabric to be defined by a combination of fabric elements, as shown in Figures 1 and 4.
Tabular mineral grains:
Platy or flake-shaped mineral grains like mica are often aligned to produce a foliation.
Less obviously, tabular mineral grains may contribute to lineation if their orientations are scattered so that their planes all include a particular line.
Acicular mineral grains:
Needle-shaped, or acicular, mineral grains like amphibole and sillimanite are often aligned to produce a lineation.
Less obviously, needle-shaped mineral grains may contribute to foliation if they are distributed parallel to a plane.
Crystallographic preferred orientation (CPO):
Sometimes it is necessary to look at thin section under the microscope to see a fabric. If the crystallographic axes of a particular mineral are all parallel to a particular plane or line, then the rock has a fabric. Typically this will only become obvious when the microscope stage is rotated between crossed polars, especially when a 1-lambda plate is inserted; all the grains change colours ‘in sync’ as the stage is rotated.
Domains:
A domain is a region within a rock that has a distinctive composition or texture. Flattened clasts in a sedimentary rock can produce a foliation if they are all aligned to a plane. Stretched clasts in a sedimentary rock can produce a lineation if they are all aligned parallel to a line.
Layers:
Layers are really just domains that are very extensive and parallel-sided.
Rods:
Rods are really just domains that are very elongated and continuous.
Cracks and discontinuities:
Closely spaced fractures can produce a type of cleavage called fracture cleavage.
Fold hinges:
Numerous closely spaced fold hinges may produce a lineation in highly deformed rocks. This structure is called a crenulation lineation.
Fold axial surfaces:
Numerous closely spaced fold axial surfaces define a fabric called called crenulation cleavage, because the axial surfaces may be planes of weakness along which a rock tends to split.
Intersecting foliations:
Whenever two intersecting foliations are present, there is always an intersection lineation defined by their intersection. In the field, although it’s possible to calculate the intersection lineation from strike-and-dip measurements of the two foliations, it’s usually much more accurate to measure the lineation directly.
Common types of foliation, and their origins

Primary fabrics:
Sedimentary rocks are typically recognized by their primary fabrics. Actually, two types of fabric are common:
- Bedding and lamination are defined by layers of different composition or texture, typically reflecting environmental change during deposition;
- Fissility is a fabric characteristic of mudrocks, in which the sheet silicates have been aligned by compaction to produce a penetrative primary foliation.

Slaty cleavage:
Slaty cleavage is a penetrative fabric in which micas or other sheet silicates, below the limit of visibility with the naked eye, are aligned parallel to a plane, which becomes an easy plane of splitting. Strain studies have shown that slaty cleavage typically forms perpendicular to the direction of maximum shortening, the Z axis of the strain ellipsoid. In other words, cleavage forms parallel to the X-Y plane. Some slaty cleavages are penetrative down to the scale of individual mineral grains; others show domains under the microscope.
Cleavage is thought to develop by a combination of processes including:
- Physical rotation (transposition) of mineral grains as a rock is deformed;
- Solution of grains subjected to high stress (pressure solution);
- Growth of new mineral grains during deformation.
Slaty cleavage is the defining characteristic of the rock-type slate.
Schistosity:
Schistosity is a coarser grained version of slaty cleavage, and is the term used for a more or less penetrative foliation defined by mineral grains coarser than about 1 mm. Many geologists actually recognize an intermediate feature phyllitic foliation, when the fabric-defining minerals are just visible. However, the boundaries between these categories have never been formally defined.
Schistosity involves the same types of process as slaty cleavage, but is typical of higher metamorphic grades and always involves significant new mineral growth.
Gneissic banding:
Gneissic banding is developed as a result of recrystallization during medium- to high-grade metamorphism. It is characterized by the preferred orientation of platy, tabular, or prismatic minerals, and by subparallel lenticular mineral grains and grain aggregates. Most gneisses also display compositional (mafic/felsic) banding.
Flattening fabric:
When a foliation is defined by domains that represent identifiable deformed objects in a rock, such as flattened pebbles in a deformed conglomerate, the fabric can be called a flattening fabric. (Most foliations are probably produced by flattening, but this term is used when the origin is obvious.)

Pressure-solution cleavage:
Sometimes deformed rocks contain domains or layers of different composition that can be shown to have originated as a result of solution of particular minerals. For example, quartz may be preferentially dissolved from certain bands within a rock, producing mica-rich seams that separate quartz-rich lithons.
Crenulation cleavage:
Crenulation cleavage is defined by closely spaced fold axial surfaces. It’s almost always a second or later generation of fabric: an initial deformation produces a foliation and later deformation folds that foliation to produce a crenulation cleavage.
Sometimes crenulation cleavage is combined with pressure solution to produce differentiated crenulation cleavage.
Mylonitic foliation:
Extreme ductile shearing in shear zones tends to reduce the grain size of mineral grains, while stretching the original grains out into domains of extreme dimensions, and also producing strong crystallographic preferred orientation. This type of foliation is called mylonitic foliation. It’s almost always accompanied by a lineation, producing an LS-fabric.
Relationships of foliations to folds
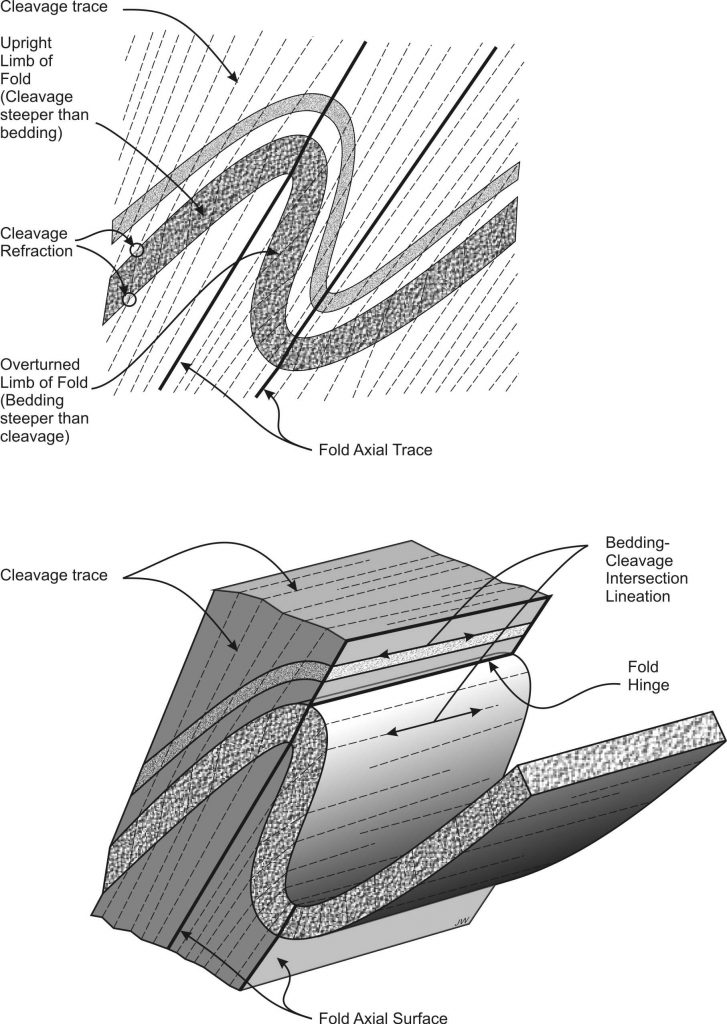
Foliations are often developed parallel, or roughly parallel, to the axial surfaces of folds (Fig. 3). This relationship is common because both structures originate from the same strain. Fabric planes and fold axial surfaces are perpendicular to the shortening direction, the short axis of the strain ellipsoid (Z). Foliation of this type is called axial planar foliation (or axial planar cleavage, etc. depending on the type of foliation.)
In detail, axial planar foliations often depart from exact parallelism with the axial surface of a fold, because of local strain variation. One very common style is called cleavage refraction (Fig. 5) in which cleavage bends so that it is more perpendicular to competent layers, and more parallel to incompetent layers.
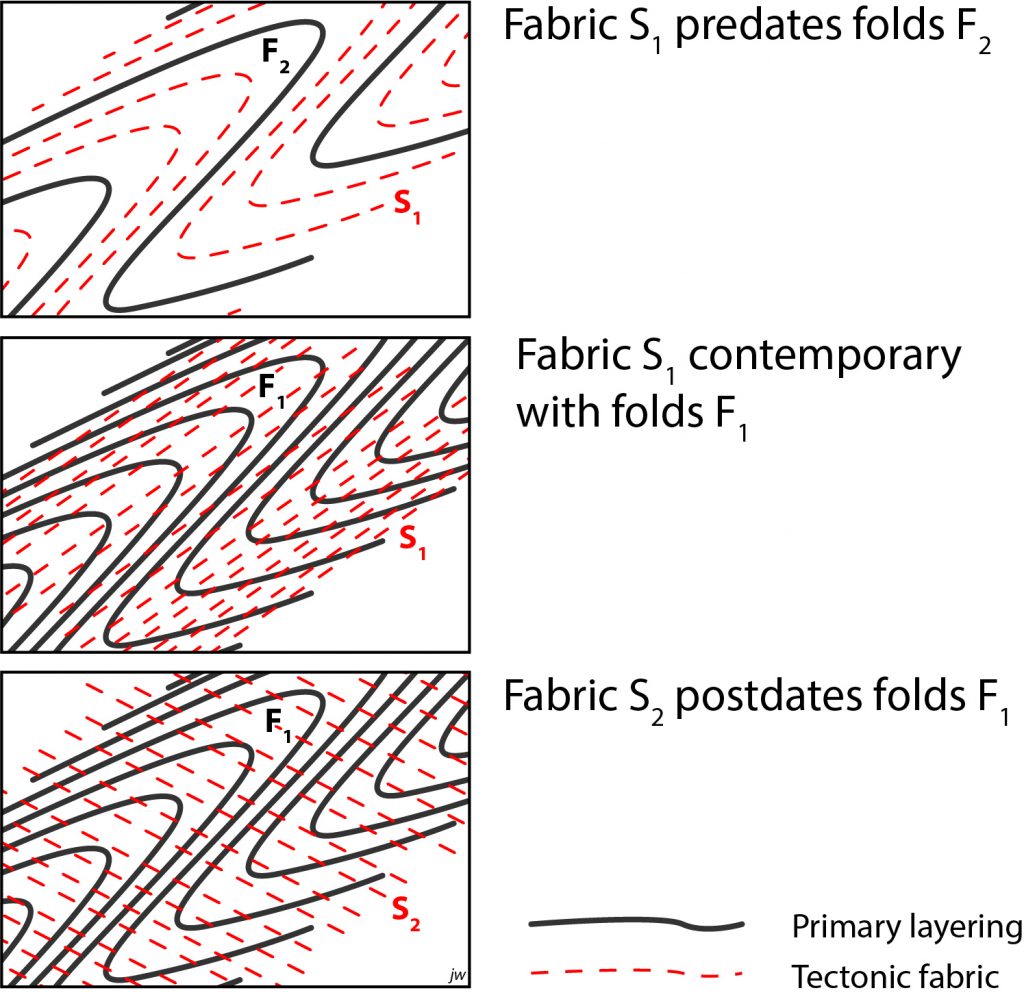
The axial planar relationship is very useful when disentangling superimposed folds. It’s conventional to number fold generations, starting with the earliest, as F1, F2, F3 etc. The corresponding axial planar foliations are called S1, S2 etc., where S1 is axial planar to F1, but is folded by F2. Sometimes the numbering scheme is even extended to bedding, which is labelled S0.
Common types of lineation, and their origins
Primary lineations: Primary lineations are less common than primary foliations. Typically, primary lineations in sedimentary and igneous rocks both reflect flow direction.
Mineral lineations: Mineral lineations are the linear equivalent of slaty cleavage and schistosity. Strain studies suggest that mineral lineations typically form parallel to the direction of maximum extension, the S1, or X axis of the strain ellipsoid. Like their planar counterparts. they probably form by a combination of grain rotation, solution, and grain growth during deformation.

Stretching lineation: When a lineation is defined by domains that represent identifiable deformed objects in a rock, such as stretched pebbles in a deformed conglomerate, the fabric can be called a stretching lineations.

Crenulation lineation: Crenulation cleavage is defined by closely spaced fold hinges. It’s almost always a second or later generation of fabric: an initial deformation produces a foliation and later deformation folds that foliation to produce a crenulation lineation. Crenulation lineation is almost always visible when crenulation cleavage is present.

Mylonitic lineation: Extreme ductile shearing in shear zones tends to reduce the grain size of mineral grains, while stretching the original grains out into domains of extreme dimensions, and also producing strong crystallographic preferred orientation. This variety of stretching lineation is called mylonitic lineation. It’s almost always accompanied by a foliation, producing an LS-fabric.
Intersection lineation: Whenever two intersecting foliations are present, there is always an intersection lineation defined by their intersection. In the field, although it’s possible to calculate the intersection lineation from strike-and-dip measurements of the two foliations, it’s usually much more accurate to measure the lineation directly.

Relationship of lineation to folds
In folds with axial planar foliations, an intersection lineation is formed where the cleavage planes cut through the folded surfaces. If the folds are reasonably cylindrical, this intersection lineation is parallel to the fold axis. Measuring the intersection lineation is therefore a valuable way of finding fold axis orientations in areas where fold hinges are not well exposed.
Sometimes a second lineation can be seen in folded rocks with axial planar slaty cleavage. This lineation takes the form of faint streaks on the cleavage surfaces at a high angle to the fold hinges. It’s sometimes called a down-dip lineation from its orientation in areas of gently plunging folds. It probably originates as a stretching lineation, and represents the long axis of the strain ellipsoid (X).
In higher grade rocks, sometimes stretching lineations (or mineral lineations thought to be formed by stretching) are found parallel to fold hinges. This is usually an indication that extreme shearing has occurred, with the generation of sheath folds. These will be considered in more detail when we deal with mylonites later in the course.
In areas with multiple generations of fabrics and folds, lineations are typically numbered L1, L2 etc., to correspond with fold and foliation generations.


