1.9: Dynamic Analysis- Stress
- Page ID
- 12516
Introduction
Dynamics is the part of structural geology that involves energy, force, stress, and strength.
It’s very important to distinguish dynamic concepts from kinematic ones. Many mistakes have been made in structural geology by people who have tried to do dynamic analysis without first understanding how things have moved (kinematics). Although words like stress and strain have very similar meanings in everyday life, their scientific meanings are very different. Stress is a dynamic term whereas strain is purely kinematic.
Even in everyday life, it’s difficult to measure a force or stress directly. For example, when you stand on a bathroom scale, you are deforming a spring (that’s strain!). It is only because the spring has very precisely known dynamic properties (stress and strain are proportional for the spring) that we can use that strain to infer something about your weight. In geology, our knowledge of the stress-strain relationship for rocks (especially when buried deep in the crust and deformed over millions of years) is quite patchy. Be careful, when using dynamic terms, that you really know what are you are talking about!
Force and stress
Units of force
Force is measure in Newtons where 1 N is the force necessary to accelerate a mass of 1 kg by 1 m/s2.
Units of stress
In structural geology we are almost always interested in what a force does to some part of the Earth’s crust, so we need a measure of force concentration or force per unit area. This is stress.
Note: some textbooks define two different quantities: traction is the force per unit area on a single plane, a vector quantity; stress is the total of forces acting on all possible planes that pass through a point in the Earth’s crust, a tensor quantity. At this level we refer to both concepts as ‘stress’; the sense is almost always clear from the context.
The unit of stress is 1 N/m2 or 1 Pa (Pascal).
1 Pascal isn’t enough to do detectable damage to any kind of rock. More useful units are:
1000 Pa = 1 kPa
106 Pa = 1 MPa
109 = 1 GPa
1 GPa is roughly the pressure at the base of the crust, about 30 km down.
An older unit of stress is the bar.
1 bar = 105 Pa or, more usefully 10 kbar = 1 GPa
There are other units out there. You may encounter the atmosphere (atm), and the pound per square inch (psi)
1 atm = 1.01 bar = 10100 Pa
1 psi = 690 Pa
All these units can be used to describe pressure. Pressure is the state of stress in a stationary fluid, like water. In fact, pressure is also known as hydrostatic stress. Hydrostatic stress is the type of stress experienced by a submerged submarine. Each 1 m2 of the skin of the submarine experiences the same force, acting perpendicular to that surface.
Stress on a plane (a.k.a. traction)
In solids, the situation is more complex. Each surface of a mineral grain within the Earth experiences a different force concentration depending on its orientation. Also, some surfaces experience forces that are not perpendicular to the surface.
In fact, we can resolve the force per unit area (a vector) on a surface into two components.
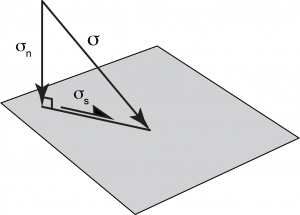
Normal stress, also known as normal traction σn is the part of that stress that acts perpendicular to the surface. Shear stress also known as shear traction σs is the part that acts parallel to the surface.
Because most normal stresses within the Earth act inward, geologists represent compressive normal stress as positive, and use negative numbers for tensile stresses. When we start talking about stress and strain, this can cause confusion, because positive stress (inwards) tends to cause negative extension (ie shortening) and vice versa. (Engineers often use the opposite convention, which is mathematically more logical, but requires pressure to be a negative quantity, which is less intuitive for most people).
State of stress at a point
For any given orientation (strike and dip) of a surface passing through a given point in the crust, there is a different value of normal and shear stress. At first sight this is a bewildering mess of forces, all acting in different directions at the same point, but there are some relationships between the various forces that simplify things.
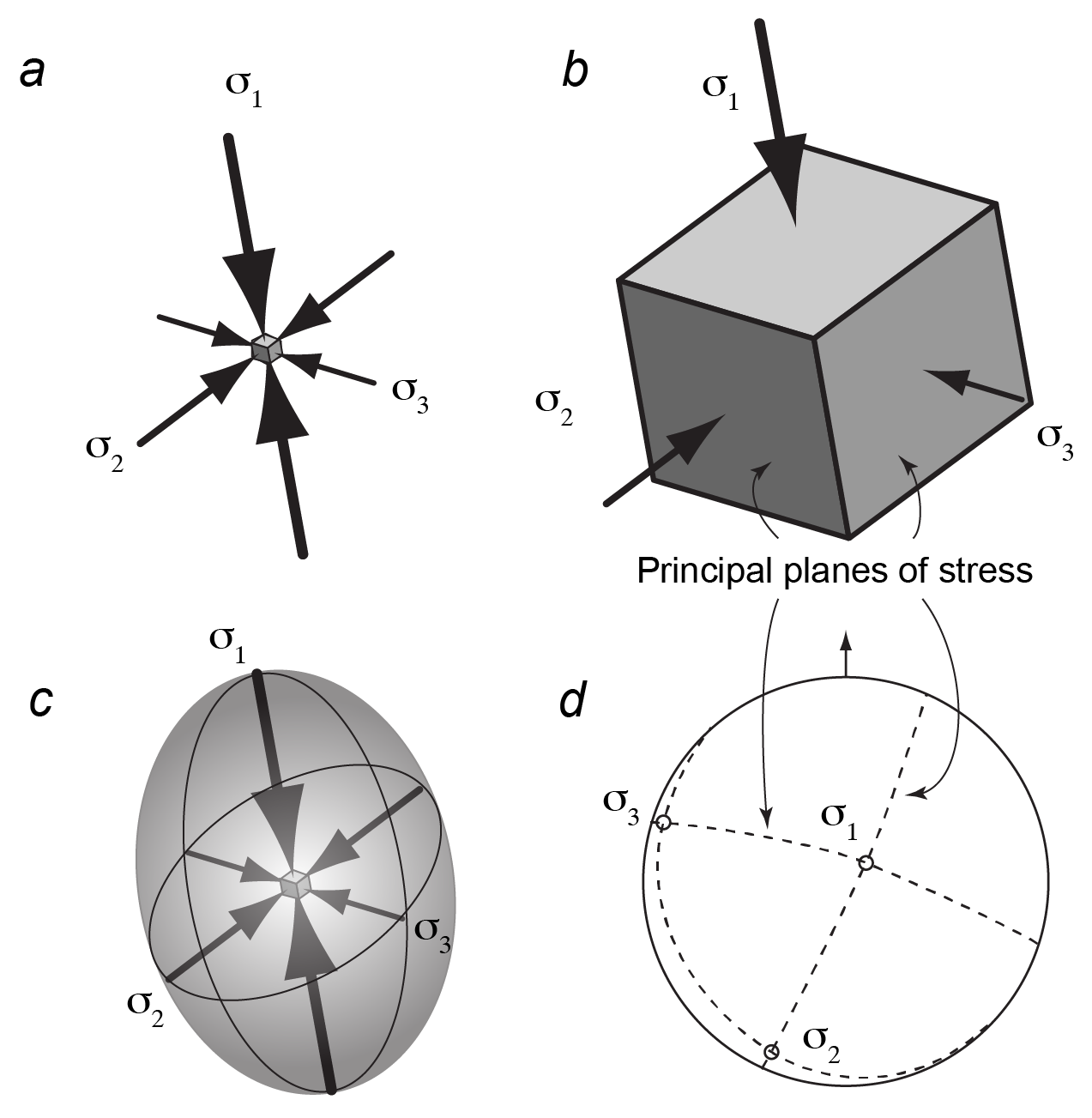
First, if we represent all the stresses acting on all the surfaces as vectors, drawn as arrows, the tails of those arrows make an ellipse (in 2-D) or an ellipsoid (in 3-D). The ellipsoid is called the stress ellipsoid.
Second, it’s possible to prove that there are always three mutually perpendicular planes that experience no shear stress. These are principal planes of stress. The normal stresses they experience are the maximum, minimum, and an intermediate value of normal stress. We call them principal stresses and label them, in order:
σ1 > σ2 > σ3
The directions of the principal stresses are called the stress axes.
You may have noticed that there are close analogies between stress and strain. Be careful not to confuse them! Stress is dynamic; strain is kinematic!
Hydrostatic and lithostatic stress
Hydrostatic stress is the special case where σ1 = σ2 = σ3 and is equivalent to ‘pressure‘ in a fluid. Where the pressure is due to overlying rock, not fluid, the term lithostatic stress is sometimes used.
Non-hydrostatic and differential stress
In much of the Earth’s crust, the state of stress is non-hydrostatic. However, pressure is still a useful concept. What we mean by pressure under those circumstances is mean stress. The mean stress is the average of the three principal stresses.
σm = (σ1 > σ2 > σ3 )/3
The mean stress is the part of the stress that acts to change volume. It’s the most important type of stress for metamorphic petrologists, because high mean stress (high pressure) tends to produce dense minerals like garnet and glaucophane.
What about the rest of the stress? If we subtract the mean stress from each of the principal stresses, we get a “left over” stress system called the deviatoric stress defined by principal values.
σ1 = σm , σ2 = σm , σ3 = σm
The deviatoric stress is the part of the stress that acts to change shape, and is the part of greatest interest to structural geologists.
A related concept is the differential stress. This is just the difference between the largest and the smallest principal stress: σd = σ1 – σ3.
Effective stress
A final concept to be aware of in dynamic analysis is that of effective stress. In porous rock, the pore spaces are typically filled with fluid, often water, but sometimes oil or natural gas. If that fluid is itself under pressure, it partially supports the mineral grains, and reduces the stresses between the solid parts of the rock, making them behave as if they were located at a shallower depth. The effective stress is the true stress minus the fluid pressure. It is the part of the stress that acts within the solid components of a porous rock.
Stress regimes
The Earth’s surface is approximately a plane of zero shear stress (give or take a few ocean currents and wind storms). For this reason, near the Earth’s surface, one of the principal stresses is approximately vertical, and the other two are approximately horizontal.
This idea was first promoted by Scottish geologist William Masson Anderson in 1905, and has become known as the Andersonian theory of stress. Anderson distinguished three near-surface tectonic regimes depending on which stress axis was vertical.
σ1 vertical: Gravity regime
σ2 vertical: Wrench regime
σ3 vertical: Thrust regime
In a general way, these three regimes correspond respectively to typical states of stress near the three types of plate boundary: spreading centres, transform faults, and subduction zones.
Stress-strain relationships
Experimental vs. geological strain rates
Experimental rigs are used to study the types of stress that are necessary to produce different kinds of strain in rocks. A great deal has been learned from such experiments. However, it’s important to realize one major limitation: time. Geological strain rates are of the order of 10-12 – 10-15 strains per second. In the lab, if we don’t want to run our experiments for hundreds of years, it’s not feasible to achieve strain rates much below 10-8 strains per second. To get geologically meaningful results we have to extrapolate experiments to much slower strain rates.
Elastic
When rocks are subjected to small strains at low confining pressure (or mean stress) we find that the stress is proportional to the strain, and the strain is recoverable (i.e. it goes away when the stress is removed).
This type of stress-strain relationship is called elastic. The elastic behaviour or rocks allows them to store strain energy and to transmit seismic waves.
Brittle
As stress and strain are increased, eventually most rocks undergo a catastrophic loss of strength, with the release of stored strain energy. In an experiment this is called brittle fracture or brittle failure. In an experimental rig the result is a loud bang and the sample disintegrates. In the Earth’s crust the result is an earthquake.
Plastic
If the confining pressure is higher still, or the temperature is raised, a different type of behaviour occurs. After an initial phase of elastic deformation, the sample starts to deform in a ductile manner: it flows without breaking. This deformation is also non-recoverable, but it occurs without complete loss of strength. The sample shortens in the σ1 direction, and thickens parallel to σ3.
In ideal plastic behaviour, a sample shows no deformation at all until a certain stress (yield stress) is reached. Thereafter, it deforms freely so that however much shortening is imposed by the rig, it’s impossible to get the stress to go any higher.
Real rocks are a bit more complicated than the ideal. They typically show some elastic deformation below the yield stress, and with continuing plastic deformation the stress may rise a little or fall a little.
Viscous
At temperatures close to their melting point, some rocks show a much simpler type of flow behaviour without a yield stress. In viscous behaviour, any small amount of stress will cause strain to start. The strain rate is proportional to the stress. Viscous behaviour is sometimes also called Newtonian. Water, air, magmas, and rock salt may show approximately Newtonian behaviour.
Competence
What controls how a given rock will respond to stress? Several variables control the specific response in a given situation. Confining stress (or mean stress, roughly equivalent to the concept of ‘pressure’) is one of these variables; mean stress increases with depth within the Earth. Temperature exerts a tremendous influence on rock strength, and also typically increases with depth according to the geothermal gradient. The strain rate, which is the rate at which the rocks are being deformed, is a third variable. Finally, the rock composition exerts considerable influence as well.
For each of the above idealized types of behaviour, there is a parameter that measures a rock’s strength, or resistance to stress. For elastic deformation it is called Young’s modulus; for brittle behaviour it is the differential stress at failure; for plastic deformation it’s the yield stress; and for viscous behaviour it’s the viscosity.
Real rocks show complicated mixtures of these behaviour types, making these quantities very hard to measure. Nonetheless, in the field we can often recognize rock types that have undergone more strain, and those that have undergone less, side by side in the same outcrop (where they have presumably had very similar stress histories). Under these circumstances it’s useful to have a general term for resistance for stress. That term is competence. For example, if we observe that layers of slate have undergone a lot more strain than interbedded quartzite layers, we might deduce that the quartzite was more competent.


