1.4.1: Latitude and Longitude
- Page ID
- 15340
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)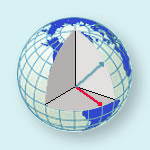
Latitude and longitude comprises a grid system of lines encircling the globe and is used to determine the locations of points on the earth. Lines of latitude, also called parallels, run east - west. Latitude lines always run parallel to each other, and hence, they are always an equal distance apart. Latitude lines never converge or cross.
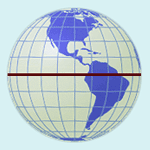
Lines of latitude measure distance north or south of the equator. The latitude of a particular location is the distance, measured in degrees, between that place and the equator along a meridian, or line of longitude. The equator is 0o latitude, and the North and South Poles are located at 90o north and 90o south latitude respectively. In other words, values for latitude range from a minimum of 0o to a maximum of 90o.
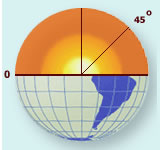
If the earth were a perfect sphere (which it isn't), the distance, or the length, of 1o of latitude would be constant everywhere. In reality, the earth is slightly flattened at the poles, so the length of 1o of latitude at the poles is slightly more than at the equator. At the equator, the length of 1o of latitude is equal to 110.6 km (68.7 mi.) and at the poles, the length of 1o of latitude is equal to 111.7 km (69.4 mi.). For our purposes, we will assume the length of one degree of latitude is 111 km.
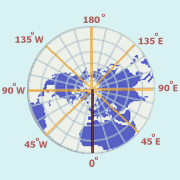
Lines of longitude, also called meridians, run north - south. Meridians are farthest apart at the equator, and converge at the North and South Poles. Lines of longitude measure distance east or west of the prime meridian. The longitude of a particular location is the distance along a parallel, measured in degrees, between that place and the prime meridian. The prime meridian passes through the old Royal Observatory at Greenwich, England, and is sometimes referred to as the Greenwich meridian. Since meridians are farthest apart at the equator and converge at the poles, the distance in kilometers (or miles) of 1o of longitude varies from a maximum at the equator, to a minimum at the poles. At the equator the approximate length of 1o is approximately 111 km (69 mi.). At 60o north and south latitudes, the length of 1o of longitude is approximately 55.5 km (34.5 mi.), or half what it is at the equator.
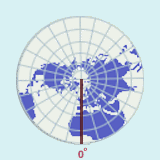
The prime meridian, which runs through Greenwich, England, is referred to as 0o longitude. Points are measured east or west of the prime meridian until one reaches the opposite side of the prime meridian, which is referred to as the International Date Line. This is considered 180o longitude, and is the highest value which longitude can take. In other words, values for longitude range from a minimum of 0o to a maximum of 180o.
An infinite number of parallels or meridians can be drawn on a globe. Thus, parallels and meridians exist for any point on the earth. Generally, only selected parallels and meridians are marked on maps and globes, and these are usually spaced equal distances apart. Parallels and meridians always intersect each other at right angles. In order to locate a particular point on the earth, a latitude and a longitude measurement is necessary. As stated above, these measurements are in degrees, but sometimes measurements smaller than degrees are necessary. In this case, minutes and seconds are used.
When we travel, we usually like to take the shortest route between two locations. If you pass a plane through the center of a sphere, the intersection of the plane and the surface of the sphere creates a great circle. Planes passing through any other part of a sphere without going through the center create small circles. An arc of a great circle is the shortest distance between two points on a sphere and therefore is the preferred route for planes traveling great distances, like crossing an ocean. The concept of great and small circles relates to meridians (longitude) and parallels (latitude). Meridians are half of a great circle (180o) whose ends are at the North and South poles. Parallels of latitude are small circles, except for the equator which is a great circle.
(Source: Wikipedia)
(Source: Wikipedia)
For more information about other locational systems, start "Digging Deeper Into Locational Systems: USPLS and UTM" or continue reading
United States Public Land Survey (USPLS)
Latitude and longitude gives us an easy way of locating points on the Earth. Instead of a point, we may wish to identify land areas. In the United States, the United States Public Land Survey (USPLS), conceived by Thomas Jefferson, is used to identify parcels of land. The USPLS is actually a means of describing parcels of land, but like latitude and longitude, the USPLS is basically a grid that can be used to identify location.

Across the United States, several principal meridians (lines of longitude) have been selected to define "columns" of ranges every six miles either east or west of a particular principal meridian. In a similar fashion, "rows" of townships are delimited every six miles either north or south of a particular baseline, that coincides with a line of latitude. This creates a grid work of townships and ranges encompassing 36 square miles in area. Actually, an individual cell in this grid is sometimes referred to simply as a township.
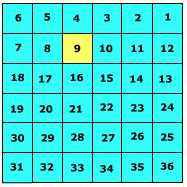
A township is subdivided into 36 1 square mile sections. Sections are numbered beginning at the upper right and working left to section 6, then down to 7, and then right across to section 12 ending with 36 sections as shown in Figure \(\PageIndex{9}\).
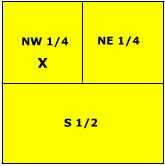
Each section is 640 acres in size and can be further subdivided into smaller units by either halving or quartering the section (Figure EG.16) and described according to direction. For instance, the letter X is located in the NW 1/4, S9, T2N, R3E.
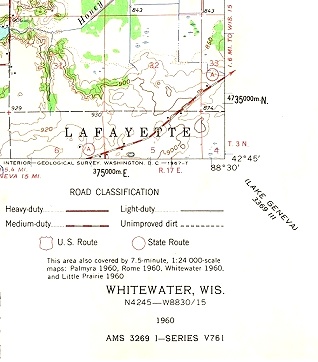
All United States Geological Survey topographic maps show the township, range, and section information on them. the figure below is a portion of the Whitewater, WI 1:24000 USGS topographic map. Township and Range information is found printed in red along the bottom and left margins (R 17E, T3N). Section boundaries are printed in red and their number designation is printed in the center of the section.
The Universal Transverse Mercator (UTM) Grid
Though a spherical coordinate system like latitude and longitude is convenient for large areas, it is cumbersome for small areas. The need for accurate measurements within small areas was realized with the increasing range of artillery during the First and Second World Wars. This spurred the development of rectangular coordinate grid systems as plane rectangular geometry formulas were simpler than spherical geometry formulas upon which latitude and longitude is derived from. The Universal Transverse Mercator (UTM) Grid is one such system.
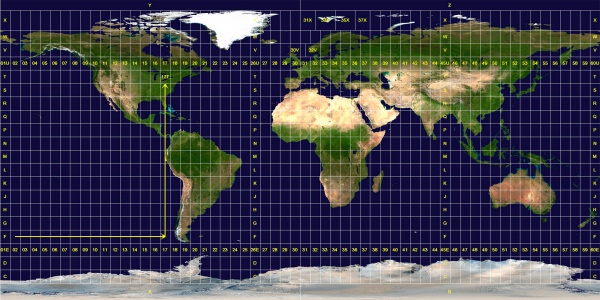
The Universal Transverse Mercator Grid divides the world into 60 north-south zones, each covering a strip 6° wide in longitude between 84N and 80S. Poleward the Universal Stereographic grid (UPS) is used. These longitude zones are numbered (called the "zone number") from Zone 1, between 180° and 174° west longitude, progressing eastward to Zone 60, between 174° and 180° east longitude. Each longitude zone is subdivided into a latitude zone is 8 degrees high north and south of the equator, and lettered starting from "C" at 80° S, increasing up to "X" (called the "zone designator"). The letters "I" and "O" are omitted because of their similarity to the digits one (1) and zero(0). X spans 12° of latitude.
Each longitude zone is subdivided into an eastern and western half by drawing a line down the middle called the "central meridian". A point can be described by its distance east of the origin, called its "easting" value. The central meridian is assigned a false easting of 500,000 meters to insure positive coordinates. Any easting value greater than 500,000 meters indicates a point east of the central meridian. Any easting value less than 500,000 meters indicates a point west of the central meridian. A point's north-south origin depends on the hemisphere it is in. In the northern hemisphere, the origin is the equator and all distances north (or ‘northings’) are measured from the equator. In the southern hemisphere the origin is the south pole and all northings are measured from there. When writing UTM coordinates, the easting is always first and the northing is after it.
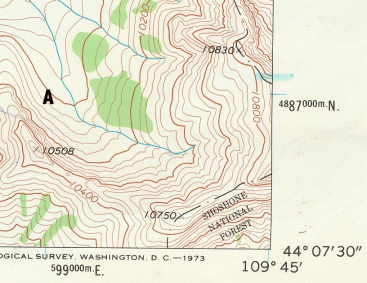
The UTM grid is printed on all U.S. Geological Survey (USGS) maps as blue tick marks in the margins, or as full grid lines. The spacing of the tick marks or grid lines depends on the scale of the map. Point A on the topopgraphic map is located at 599000 E., 4887000 N.


