1.3.6: The Global Positioning System (GPS)

Last updated
Save as PDF

Page ID: 15339

Michael E. Ritter
University of Wisconsin-Stevens Point via The Physical Environment

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The Global Positioning System consists of three parts:

Earth orbiting satellites,
control and monitoring stations across the Earth, and
GPS receivers owned by individuals.

A set of 24 satellites orbiting the Earth every 12 hours broadcasting their position and time. A ground-based receiver listens to the signals from four or more satellites, comparing the time transmissions of each with its own clock. Given that signal travels at a known rate of speed, the receiver can calculate the distance between the satellite and receiver. Combining the position of the satellite at the time of transmission with the distance, the receiver is able to determine its location.

Figure \(\PageIndex{1}\): The constellation of GPS satellites (Courtesy USGS)

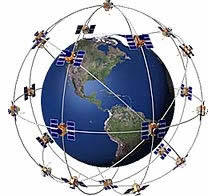
Differential GPS uses a base station of an exact known location and a mobile unit to determine position. GPS determines location by computing the difference between the time that a signal is sent by a satellite and the time it is received by a GPS receiver. The base station calculates its position from satellite signals and compares this location to the known location. The base station broadcasts the range errors they're seeing from GPS satellites to the remote receiver. The mobile receiver uses these correction messages, correlated with the satellite signals its receiving, to determine position.

Figure \(\PageIndex{2}\): GPS ground receiver on the flank of Augustine Volcano (Cook Inlet, Alaska) Courtesy USGS

GPS is being employed in a variety of ways. GPS is widely used for ground, air, and sea navigation. It is used to produce highly accurate maps and record land deformation caused by earthquakes and volcanic eruptions. GPS is showing up in a number of commercial products available to the public from standalone units to automobiles, cell phones, and digital cameras interfaces. A popular use of gps units is geocaching, a high-tech "treasure" hunting game.

Assess your basic understanding of the preceding material by "Looking Back: Tools of the Geographer" or continue reading.