3.1: Discovering How Populations Change
- Page ID
- 11758
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)All species of living organisms—from the bacteria on our skin, to the trees in our yards, to the birds outside—evolved at some point from a different species. Although it may seem that living things today stay much the same from generation to generation, that is not the case: evolution is ongoing. Evolution is the process through which the characteristics of species change and through which new species arise.
The theory of evolution is the unifying theory of biology, meaning it is the framework within which biologists ask questions about the living world. Its power is that it provides direction for predictions about living things that are borne out in experiment after experiment.
Charles Darwin and Natural Selection
The actual mechanism for evolution was independently conceived of and described by two naturalists, Charles Darwin and Alfred Russell Wallace, in the mid-nineteenth century. Importantly, each spent time exploring the natural world on expeditions to the tropics. From 1831 to 1836, Darwin traveled around the world on H.M.S. Beagle, visiting South America, Australia, and the southern tip of Africa. Wallace traveled to Brazil to collect insects in the Amazon rainforest from 1848 to 1852 and to the Malay Archipelago from 1854 to 1862. Darwin’s journey, like Wallace’s later journeys in the Malay Archipelago, included stops at several island chains, the last being the Galápagos Islands (west of Ecuador). On these islands, Darwin observed species of organisms on different islands that were clearly similar, yet had distinct differences. For example, the ground finches inhabiting the Galápagos Islands comprised several species that each had a unique beak shape (Figure below). He observed both that these finches closely resembled another finch species on the mainland of South America and that the group of species in the Galápagos formed a graded series of beak sizes and shapes, with very small differences between the most similar. Darwin imagined that the island species might be all species modified from one original mainland species. In 1860, he wrote, “Seeing this gradation and diversity of structure in one small, intimately related group of birds, one might really fancy that from an original paucity of birds in this archipelago, one species had been taken and modified for different ends.”
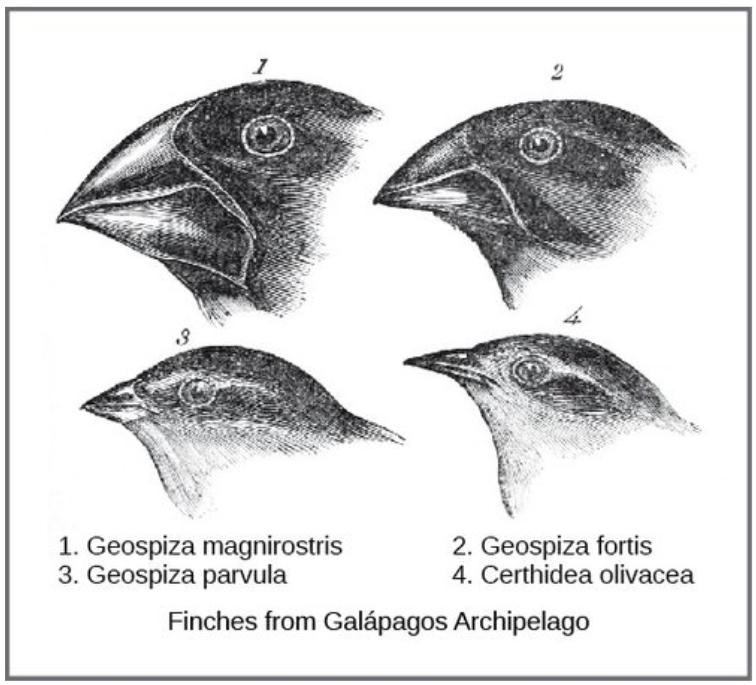
Figure \(\PageIndex{1}\): Darwin observed that beak shape varies among finch species. He postulated that the beak of an ancestral species had adapted over time to equip the finches to acquire different food sources. This illustration shows the beak shapes for four species of ground finch: 1.Geospiza magnirostris (the large ground finch), 2. G. fortis (the medium ground finch), 3. G. parvula (the small tree finch), and 4. Certhidea olivacea (the green-warbler finch).
Demonstrations of evolution by natural selection can be time consuming. One of the best demonstrations has been in the very birds that helped to inspire the theory, the Galápagos finches. Peter and Rosemary Grant and their colleagues have studied Galápagos finch populations every year since 1976 and have provided important demonstrations of the operation of natural selection. The Grants found changes from one generation to the next in the beak shapes of the medium ground finches on the Galápagos island of Daphne Major. The medium ground finch feeds on seeds. The birds have inherited variation in the bill shape with some individuals having wide, deep bills and others having thinner bills. Large-billed birds feed more efficiently on large, hard seeds, whereas smaller billed birds feed more efficiently on small, soft seeds. During 1977, a drought period altered vegetation on the island. After this period, the number of seeds declined dramatically: the decline in small, soft seeds was greater than the decline in large, hard seeds. The large-billed birds were able to survive better than the small-billed birds the following year. The year following the drought when the Grants measured beak sizes in the much-reduced population, they found that the average bill size was larger (Figure below). This was clear evidence for natural selection (differences in survival) of bill size caused by the availability of seeds. The Grants had studied the inheritance of bill sizes and knew that the surviving large-billed birds would tend to produce offspring with larger bills, so the selection would lead to evolution of bill size. Subsequent studies by the Grants have demonstrated selection on and evolution of bill size in this species in response to changing conditions on the island. The evolution has occurred both to larger bills, as in this case, and to smaller bills when large seeds became rare.
Figure \(\PageIndex{3}\): A drought on the Galápagos island of Daphne Major in 1977 reduced the number of small seeds available to finches, causing many of the small-beaked finches to die. This caused an increase in the finches’ average beak size between 1976 and 1978.
Variation and Adaptation
Natural selection can only take place if there is variation, or differences, among individuals in a population. Importantly, these differences must have some genetic basis; otherwise, selection will not lead to change in the next generation. This is critical because variation among individuals can be caused by non-genetic reasons, such as an individual being taller because of better nutrition rather than different genes.
Genetic diversity in a population comes from two main sources: mutation and sexual reproduction. Mutation, a change in DNA, is the ultimate source of new alleles or new genetic variation in any population. An individual that has a mutated gene might have a different trait than other individuals in the population. However, this is not always the case. A mutation can have one of three outcomes on the organisms’ appearance (or phenotype):
- A mutation may affect the phenotype of the organism in a way that gives it reduced fitness—lower likelihood of survival, resulting in fewer offspring.
- A mutation may produce a phenotype with a beneficial effect on fitness.
- Many mutations, called neutral mutations, will have no effect on fitness.
Mutations may also have a whole range of effects on the fitness of the organism that expresses them in their phenotype, from a small effect to a great effect. Sexual reproduction and crossing over, which occurs in meiosis, also lead to genetic diversity: when two parents reproduce, unique combinations of alleles assemble to produce unique genotypes and, thus, phenotypes in each of the offspring.
A heritable trait that aids the survival and reproduction of an organism in its present environment is called an adaptation. An adaptation is a “match” of the organism to the environment. Adaptation to an environment comes about when a change in the range of genetic variation occurs over time that increases or maintains the match of the population with its environment. The variations in finch beaks shifted from generation to generation providing adaptation to food availability.
Whether or not a trait is favorable depends on the environment at the time. The same traits do not always have the same relative benefit or disadvantage because environmental conditions can change. For example, finches with large bills were benefited in one climate, while small bills were a disadvantage; in a different climate, the relationship reversed.
Patterns of Evolution
The evolution of species has resulted in enormous variation in form and function. When two species evolve in different directions from a common point, it is called divergent evolution. Such divergent evolution can be seen in the forms of the reproductive organs of flowering plants, which share the same basic anatomies; however, they can look very different as a result of selection in different physical environments, and adaptation to different kinds of pollinators (Figure below).

In other cases, similar phenotypes evolve independently in distantly related species. For example, flight has evolved in both bats and birds, and they both have structures we refer to as wings, which are adaptations to flight. The wings of bats and birds, however, evolved from very different original structures. When similar structures arise through evolution independently in different species it is called convergent evolution. The wings of bats and birds are called analogous structures (Figure below); they are similar in function and appearance, but do not share an origin in a common ancestor. Instead they evolved independently in the two lineages.

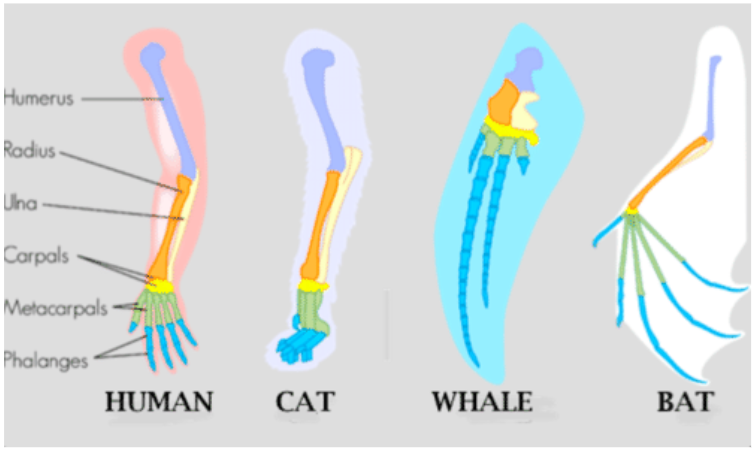
The wings of a hummingbird and an ostrich are homologous structures, meaning they share similarities (despite their differences resulting from evolutionary divergence). The wings of hummingbirds and ostriches did not evolve independently in the hummingbird lineage and the ostrich lineage—they descended from a common ancestor with wings. Figure below shows the homologous structures of several different mammals. They all have the same basic pattern of bones. They inherited this pattern from a common ancestor. However, their forelimbs now have different functions.
The Modern Synthesis
The coherent understanding of the relationship between natural selection and genetics that took shape by the 1940s and is generally accepted today is known as the modern synthesis. In sum, the modern synthesis describes how evolutionary pressures, such as natural selection, can affect a population’s genetic makeup, and, in turn, how this can result in the gradual evolution of populations and species. The theory also connects this gradual change of a population over time, called microevolution, with the processes that gave rise to new species and higher taxonomic groups with widely divergent characters, called macroevolution.
Population Genetics
There are several ways the allele frequencies of a population can change. One of those ways is natural selection. If a given allele confers a phenotype that allows an individual to have more offspring that survive and reproduce, that allele, by virtue of being inherited by those offspring, will be in greater frequency in the next generation. Since allele frequencies always add up to 100 percent, an increase in the frequency of one allele always means a corresponding decrease in one or more of the other alleles. Highly beneficial alleles may, over a very few generations, become “fixed” in this way, meaning that every individual of the population will carry the allele. Similarly, detrimental alleles may be swiftly eliminated from the gene pool, the sum of all the alleles in a population. Part of the study of population genetics is tracking how selective forces change the allele frequencies in a population over time, which can give scientists clues regarding the selective forces that may be operating on a given population. The studies of changes in wing coloration in the peppered moth from mottled white to dark in response to soot-covered tree trunks and then back to mottled white when factories stopped producing so much soot is a classic example of studying evolution in natural populations (Figure below).
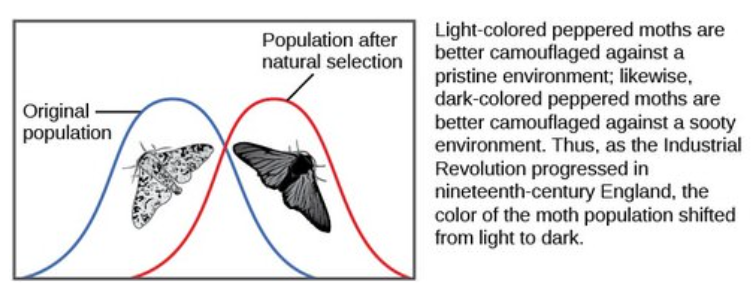
As the Industrial Revolution caused trees to darken from soot, darker colored peppered moths were better camouflaged than the lighter colored ones, which caused there to be more of the darker colored moths in the population.

