2.4: Memories of the Future- The Uncertain Art of Earthquake Forecasting
- Page ID
- 6747
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)“What’s past is prologue.”
William Shakespeare, The Tempest, Act II
“Since my first attachment to seismology, I have had a horror of predictions and of predictors. Journalists and the general public rush to any suggestion of earthquake prediction like hogs toward a full trough.”
Charles Richter, Bulletin of the Seismological Society of America, 1977
1. A Mix of Science and Astrology
Predicting the future does not sit well with most earthquake scientists, including Charles Richter, quoted above. Yet if earthquake research is to truly benefit society, it must lead ultimately to prediction, no matter how elusive that goal may be.
Society asks specialists to predict many things, not just earthquakes. How will the stock market perform? Will next year be a good crop year? Will peace be achieved in the Middle East? The answers to any of these important questions, including the chance of a damaging earthquake near you in the near future, depend on complex bits of information. For each question, experts are asked to predict outcomes, and their opinions often are in conflict. Mathematicians tell me that predicting earthquakes and predicting the behavior of the stock market have a lot in common, even though one is based on physical processes in the Earth, and the other is not.
But earthquake prediction carries with it a whiff of sorcery and black magic, of ladies with long dangling earrings in dark tents reading the palm of your hand. Geologists and seismologists involved in earthquake prediction research find themselves sharing the media spotlight with trendy astrologers, some with business cards, armed with maps and star charts. I heard about one woman on the Oregon coast who claims to become so ill before natural disasters—that have included major California earthquakes and the eruption of Mt. St. Helens—that she has to be hospitalized. After the disaster, she recovers dramatically. Jerry Hurley, a high-school math teacher in Fortuna, California, would get migraine headaches and a feeling of dread before an earthquake. His symptoms were worst when he faced in the direction of the impending earthquake. Hurley is a member of MENSA, the organization for people with high IQ, and he would just as soon somebody else had this supposed “talent.”
Some of these people claim that their predictions have been ignored by those in authority, especially the USGS, which has the legal responsibility to advise the president of the United States on earthquake prediction. They go directly to the media, and the media see a big story.
A self-styled climatologist named Iben Browning forecast a disastrous earthquake on December 3, 1990, in the small town of New Madrid, Missouri. The forecast was picked up by the media, even after a panel of experts, the National Earthquake Prediction Evaluation Council (NEPEC), had thoroughly reviewed Browning’s prediction and had concluded in October of that year that the prediction had no scientific basis. By rejecting Browning’s prediction, the nay-saying NEPEC scientists inadvertently built up the story. Browning, who held a PhD degree in zoology from the University of Texas, had based his prediction on a supposed 179-year tidal cycle that would reach its culmination on December 3, exactly 179 years after a series of earthquakes with magnitudes close to 8 had struck the region. His prediction had been made in a business newsletter that he published with his daughter and in lectures to business groups around the country. Needless to say, he sold lots of newsletters.
Despite the rejection of his prediction by the seismological establishment, Browning got plenty of attention, including an interview on Good Morning America. As the time for the predicted earthquake approached, more than thirty television and radio vans with reporting crews descended on New Madrid. School was let out, and the annual Christmas parade was canceled. Earthquake T-shirts sold well, and the Sandywood Baptist Church in Sikeston, Mo., announced an Earthquake Survival Revival.
The date of the earthquake came and went. Nothing happened. The reporters and TV crews packed up and went home, leaving the residents of New Madrid to pick up the pieces of their lives. Browning instantly changed from earthquake expert to earthquake quack, and he became a broken man. He died a few months later.
The USGS once funded a project to evaluate every nonscientific forecast it could find, including strange behavior of animals before earthquakes, to check out the possibility that some people or animals could sense a premonitory change not measured by existing instruments. Preliminary findings indicated no statistical correlation whatsoever between human forecasts or animal behavior and actual events. The project was aborted for fear that it might earn the Golden Fleece Award of then-Senator William Proxmire of Wisconsin for the month’s most ridiculous government waste of taxpayers’ money.
2. Earthquake Forecasting by Scientists
Most of the so-called predictors, including those who have been interviewed on national television, will claim that an earthquake prediction is successful if an earthquake of anymagnitude occurs in the region. Let’s say that I predict that an earthquake will occur in the Puget Sound region within a two-week period of June of this year. An earthquake occurs, but it is of M 2, not “large” by anyone’s definition. Enough M 2 earthquakes occur randomly in western Washington that a person predicting an earthquake of unspecified magnitude in this area is likely to be correct. Or say that a person predicts that an earthquake of M 6 or larger will occur somewhere in the world in June of this year. It is quite likely that some place will experience an earthquake of that size around that time. Unless damage is done, this earthquake might not make the newspapers or the evening news, except that the predictor would point to it as a successful prediction ignored by the scientific establishment.
To issue a legitimate prediction, a scientist, or anyone else, for that matter, must provide an approximate location, time, andmagnitude, and the prediction must be made in such a way that its legitimacy can be checked. The prediction could be placed in a sealed envelope entrusted to a respected individual or group, which would avoid frightening the public in case the prediction was wrong. But for a prediction to be of value to society, it must be made public, but until prediction becomes routine (if it ever does), one must consider the negative impact on the public of a prediction that fails.
Prediction was one of the major goals of the federal earthquake program when it was established in 1977, and at one time it looked as if that goal might be achieved sooner than expected. In the early 1970s, a team of seismologists at Columbia University suggested that the speed of earthquake waves passing through the Earth’s crust beneath the site of a future earthquake would become slower, then return to normal just before the event. The changes in speed of earthquake waves had been noted before small earthquakes in the Adirondacks of New York State and in Soviet Central Asia.
In 1973, Jim Whitcomb, a seismologist at Caltech, reported that seismic waves had slowed down, then speeded up just before a M 6.7 earthquake in 1971 in the northern San Fernando Valley suburb of Los Angeles. Two years later, he observed the same thing happening near the aftershock zone of that earthquake: a slowdown of earthquake waves, presumably to be followed by a return to normal speed and another earthquake. Other seismologists disagreed. Nonetheless, Whitcomb issued a “forecast”—not his term, for he characterized it as “a test of a hypothesis.” If the changes in the speed of earthquake waves were significant, then there should be another earthquake of magnitude 5.5 to 6.5 in an area adjacent to the 1971 shock in the next twelve months.
My students and I happened to be doing field work on an active fault just west of the San Fernando Valley during this twelve-month period. Each night the coyotes started to howl, we would bolt upright from our sleeping bags at our campsite along the fault and wonder if we were about to have an earthquake.
Whitcomb became an overnight celebrity and was written up in People magazine. An irate Los Angeles city councilman threatened to sue both Whitcomb and Caltech. In the meantime, the predicted time span for the earthquake ran out, with no earthquake. Meanwhile, other scientists tested the Columbia University theory and found a relatively poor correlation between the variation in speed of earthquake waves in the crust and future earthquakes. (Maybe Whitcomb was right in location but off on the time and magnitude. The Northridge Earthquake struck the San Fernando Valley 23 years after the earlier earthquake; its magnitude was 6.7, larger than expected.)
At about the same time as the San Fernando “test of a hypothesis,” a prediction was made by Brian Brady, a geophysicist with the U.S. Bureau of Mines, who worked in the field of mine safety (Olson, 1989). Between 1974 and 1976, Brady published a series of papers in an international peer-reviewed scientific journal, Pure and Applied Geophysics, in which he argued that characteristics of rock failure leading to wall collapses in underground mines are also applicable to earthquakes. Brady’s papers combined rock physics and mathematical models to provide what he claimed to be an earthquake “clock” that would provide the precise time, place, and magnitude of a forthcoming earthquake. Brady observed that earthquakes in 1974 and 1975 near Lima, Peru, had occurred in a region where there had been no earthquakes for a long time, and he forecast a much larger earthquake off the coast of central Peru. Brady’s work received support from William Spence, a respected geophysicist with the USGS.
His prediction received little attention at first, but gradually it became public, first in Peru, where the impact to Lima, a city of more than seven million people, would be enormous, later in the United States, where various federal agencies grappled with the responsibility of endorsing or denying a prediction that had very little support among mainstream earthquake scientists. The prediction received major media attention when Brady announced that the expected magnitude would be greater than 9, and the preferred date for the event was June 28, 1981. The Peruvian government asked the U.S. government to evaluate the prediction that had been made by one of its own government scientists. In response to Peru’s request, a NEPEC meeting was convened in January 1981, to evaluate Brady’s prediction and to make a recommendation to the director of the USGS on how to advise the Peruvians. The panel of experts considered the Brady and Spence prediction and rejected it.
Did the NEPEC report make the controversy go away? Not at all, and Brady himself was not convinced that his prediction had no scientific merit. An interview of Brady by Charles Osgood of CBS News shortly after the January NEPEC meeting was not broadcast until June 1981, close to the predicted arrival time of the earthquake. Officials of the Office of Foreign Disaster Assistance took up Brady’s cause, and the NEPEC meeting was described as a “trial and execution.” The NEPEC panel of experts was labeled a partisan group ready to destroy the career of a dedicated scientist rather than endorse his earthquake prediction.
John Filson, an official with the USGS, made a point of being in Lima on the predicted date of the earthquake to reassure the Peruvian public. The earthquake did not keep Brady’s appointment with Lima, Peru. It has not arrived to this day.
3. Forecasts Instead of Predictions: The Parkfield Experiment
A more sophisticated but more modest forecast was made by the USGS for the San Andreas Fault at Parkfield, California, a backcountry village in the Central Coast Ranges. Before proceeding, we must distinguish between the term prediction, such as that made by Brady for Peru, in which it is proposed that an earthquake of a specified magnitude will strike a specific region in a restricted time window (hours, days, or weeks), and the term forecast, in which a specific area is identified as having a higher statistical chance of an earthquake in a time window measured in months or years. Viewed in this way, the USGS made a forecast, not a prediction, at Parkfield.
Parkfield had been struck by earthquakes of M 5.5 to 6.5 in 1901, 1922, 1934, and 1966, and newspaper reports suggested earlier earthquakes in the same vicinity in 1857 and 1881. These earthquakes came with surprising regularity every twenty-two years, give or take a couple of years, except for 1934, which struck ten years early. The 1966 earthquake arrived not twenty-two but thirty-two years later, resuming the schedule followed by the 1922 and earlier earthquakes. The proximity of Parkfield to seismographs that had been operated for many years by the University of California, Berkeley, led to the interpretation that the last three earthquake epicenters were in nearly the same spot. Furthermore, foreshocks prior to the 1966 event were similar in pattern to foreshocks recorded before the 1934 earthquake.
Scientists at the USGS viewed Parkfield as a golden opportunity to “capture” the next earthquake with a sophisticated, state-of-the-art array of instruments. These instruments were installed to detect very small earthquakes, changes in crustal strain, changes of water level in nearby monitored wells, and changes in the Earth’s magnetic and electrical fields. The strategy was that detection of these subtle changes in the Earth’s crust might lead to a short-term prediction and aid in forecasting larger earthquakes in more heavily populated regions.
At the urging of the California Office of Emergency Services, the USGS took an additional step by issuing an earthquake forecast for Parkfield. In 1984, it was proposed that there was a 95 percent chance, or probability, that an earthquake of magnitude similar to the earlier ones would strike Parkfield sometime in the period 1987 to 1993. A system of alerts was established whereby civil authorities would be notified in advance of an earthquake. Parkfield became a natural laboratory test site where a false alarm would not have the social impact of a forecast in, say, San Francisco or Los Angeles.
The year 1988, the twenty-second anniversary of the 1966 shock, came and went with no earthquake. The next five years passed; still no earthquake. By January 1993, when the earthquake had still not occurred, the forecast was sort of, but not exactly, a failure. The 5 percent probability that there wouldn’t be an earthquake won out over the 95 percent probability that there wouldbe one.
The Parkfield forecast experiment is like a man waiting for a bus that is due at noon. Noon comes and goes, then ten minutes past noon, then twenty past. No bus. The man looks down the street and figures that the bus will arrive any minute. The longer he waits, the more likely the bus will show up. In earthquake forecasting, this is called a time-predictable model: the earthquake will follow a schedule, like the bus.
But there is another view: that the longer the man waits, the less likely the bus will arrive. Why? The bus has had an accident, or a bridge collapsed somewhere on the bus route. The “accident” for Parkfield might have been an earthquake of M 6.7 in 1983, east of Parkfield, away from the San Andreas Fault, near the oil-field town of Coalinga in the San Joaquin Valley. The Coalinga Earthquake may have redistributed the stresses building up on the San Andreas Fault to disrupt the twenty-two-year earthquake “schedule” at Parkfield.
4. The Seismic Gap Theory
Another idea of the 1970s was the seismic gap theory, designed for subduction zones around the Pacific Rim, but applicable also to the San Andreas Fault. According to theories of plate tectonics, there should be about the same amount of slip over thousands of years along all parts of a subduction zone like the Aleutians or Central America (or central Peru, for that matter, leading Brady toward his prediction). Most of the slip on these subduction zones should be released as great earthquakes. But some segments of each subduction zone have been seismically quiet a lot longer than adjacent segments, indicating that those segments that have gone the longest without an earthquake are the most likely to be struck by a future earthquake. This is a variation of the time-predictable model, of waiting for the bus. The longer you wait, the more likely the bus (or earthquake) will show up.
The San Andreas Fault ruptured in earthquakes in 1812, 1857, and 1906, and smaller earthquakes at Parkfield more frequently than that. But the southeasternmost section of the fault from San Bernardino to the Imperial Valley has not ruptured in the 230 years people have been keeping records. Paleoseismological evidence shows that the last major earthquake struck around A.D. 1680, meaning that this section has gone more than three hundred years without a major earthquake. According to the time-predictable model, this part of the fault is “nine and a half months pregnant,” to quote one paleoseismologist. Is this reach of the fault the most likely location of the next San Andreas earthquake, or have other earthquakes in the region altered the schedule, as at Parkfield?
How good is the seismic gap theory in forecasting? In the early 1990s, Yan Kagan and Dave Jackson, geophysicists at UCLA, compared the statistical prediction in 1979 of where earthquakes should fill seismic gaps in subduction zones with the actual experience in the following ten years. If the seismic gap theory worked, then the earthquakes of the 1980s should neatly fill the earthquake-free gaps in subduction zones identified in the 1970s. But the statistical correlation between seismic gaps and earthquakes of the next decade was found to be poor. Some seismic gaps had been filled, of course, but earthquakes also struck where they had not been expected, and some seismic gaps remain unfilled to this day, including the San Andreas Fault southeast of San Bernardino.
The Japanese had been intrigued by the possibility of predicting earthquakes even before a federal earthquake-research program was established in the United States. Like the early stages of the program in the U.S., the Japanese focused on prediction, with their major efforts targeting the Tokai area along the Nankai Subduction Zone southwest of Tokyo. Like the San Andreas Fault at Parkfield, the Nankai Subduction Zone appeared to rupture periodically, with major M 8 earthquakes in 1707, 1854, and a pair of earthquakes in 1944 and 1946. But the Tokai area, at the east end of the Nankai Subduction Zone, did not rupture in the 1944-1946 earthquake cycle, although it had ruptured in the previous two earthquakes. Like Parkfield, the Tokai Seismic Gap was heavily instrumented by the Japanese in search of short-term precursors to an earthquake. Unlike Parkfield, Tokai is a heavily populated area, and the benefits to society of a successful earthquake warning there would be very great.
According to some leading Japanese seismologists, there are enough geologic differences between the Tokai segment of the Nankai Subduction Zone and the rest of the zone that ruptured in 1944 and 1946 to explain the absence of an earthquake at Tokai in the 1940s. One view is that the earlier earthquakes at Tokai in 1707 and 1854 were on local crustal faults, not the east end of the subduction zone, which implies that they would have no bearing on a future subduction-zone earthquake. The biggest criticism was that the Japanese were putting too many of their eggs in one basket: concentrating their research on the Tokai prediction experiment at the expense of a broader-based study throughout the country. The folly of this decision became apparent in January, 1995, when the Kobe Earthquake ruptured a relatively minor strike-slip fault far away from Tokai (Figure 7-1). The Kobe fault had been identified by Japanese scientists as one of twelve “precautionary faults” in a late stage of their seismic cycle, but no official action had been taken.
After the Kobe Earthquake, the massive Japanese prediction program was subjected to an intensive critical review. In 1997, the Japanese concluded at a meeting that their prediction experiment was not working—but they elected to continue supporting it anyway, although at a reduced level. Similarly, research dollars are still being invested at Parkfield, but the experiment has gone back to its original goal: an attempt to “capture” an earthquake in this well-studied natural laboratory and to record it with the network of instruments set up in the mid-1980s and upgraded since then. Indeed, Parkfield has already taught us a lot about the earthquake process. In 2004, the Parkfield array did, indeed, “capture” an earthquake of M 6, which, however, arrived thirty-eight years late.

5. Have the Chinese Found the Way to Predict Earthquakes?
Should we write off the possibility of predicting earthquakes as simply wishful thinking? Before we do so, we must first look carefully at earthquake predictions in China, a nation wracked by earthquakes repeatedly throughout its long history. More than eight hundred thousand people lost their lives in an earthquake in north-central China in 1556, and another one hundred eighty thousand died in an earthquake in 1920.
During the Zhou Dynasty, in the first millennium B.C., the Chinese came to believe that heaven gives wise and virtuous leaders a mandate to rule, and removes this mandate from heaven if the leaders are evil or corrupt. This became incorporated into the Taoist view that heaven expresses its disapproval of bad rule through natural disasters such as floods, plagues, or earthquakes.
In March 1966, the Xingtai Earthquake of M 7.2 struck the densely populated North China Plain two hundred miles southwest of the capital city of Beijing, causing more than eight thousand deaths. It might have been a concern about the mandate from heaven that led Premier Zhou Enlai to make the following statement: “There have been numerous records of earthquake disasters preserved in ancient China, but the experiences are insufficient. It is hoped that you can summarize such experiences and will be able to solve this problem during this generation.”
This call for action may be compared to President Kennedy’s call to put a man on the Moon by the end of the 1960s. Zhou had been impressed by the earthquake-foreshock stories told by survivors of the Xingtai Earthquake, including a M 6.8 event fourteen days before the mainshock, fluctuations in groundwater levels, and strange behavior of animals. He urged a prediction program “applying both indigenous and modern methods and relying on the broad masses of the people.” In addition to developing technical expertise in earthquake science, China would also involve thousands of peasants who would monitor water wells and observe animal behavior. Zhou did not trust the existing scientific establishment, including the Academia Sinica and the universities, and he and Mao Zedong created an independent government agency, the State Seismological Bureau (SSB), in 1970.
Following an earthquake east of Beijing in the Gulf of Bohai in 1969, it was suggested that earthquakes after the Xingtai Earthquake were migrating northeast toward the Gulf of Bohai and Manchuria. Seismicity increased, the Earth’s magnetic field underwent fluctuations, and the ground south of the city of Haicheng in southern Manchuria rose at an anomalously high rate. This led to a long-range forecast that an earthquake of moderate magnitude might strike the region in the next two years. Monitoring was intensified, earthquake information was distributed, and thousands of amateur observation posts were established to monitor various phenomena. On December 22, 1974, a swarm of more than one hundred earthquakes, the largest of M 4.8, struck the area of the Qinwo Reservoir near the city of Liaoyang. At a national meeting held in January 1975, an earthquake of M 6 was forecast somewhere within a broad region of southern Manchuria.
As January passed into February, anomalous activity became concentrated near the city of Haicheng. Early on February 4, more than five hundred small earthquakes were recorded at Haicheng. This caused the government of Liaoning Province to issue a short-term earthquake alert. The people of Haicheng and nearby towns were urged to move outdoors on the unusually warm night of February 4. The large number of foreshocks made this order easy to enforce. Not only did the people move outside into temporary shelters, they also moved their animals and vehicles outside as well. So when the M 7.3 earthquake arrived at 7:36 p.m., casualties were greatly reduced, even though in parts of the city, more than 90 percent of the houses collapsed. Despite a population in the epicentral area of several million people, only about one thousand people died. Without the warning, most people would have been indoors, and losses of life would have been many times larger. China had issued the world’s first successful earthquake prediction.
However, in the following year, despite the intense monitoring that had preceded the Haicheng Earthquake, the industrial city of Tangshan, 220 miles southwest of Haicheng, was struck without warning by an earthquake of M 7.5-7.6. The Chinese gave an official estimate of about two hundred fifty thousand people killed. Unlike Haicheng, there were no foreshocks. And there was no general warning.
What about the mandate from heaven? The Tangshan Earthquake struck on July 28, 1976. The preceding March had seen major demonstrations in Tiananmen Square by people laying wreaths to the recently deceased pragmatist Zhou Enlai and giving speeches critical of the Gang of Four, radicals who had ousted the pragmatists, including Deng Xiaoping, who would subsequently return from disgrace and lead the country. These demonstrations were brutally put down by the military (as they would be again in 1989), and Deng was exiled. The Gang of Four had the upper hand. But after the Tangshan Earthquake, Chairman Mao Zedong died and was succeeded by Hua Guofeng. The Gang of Four, including Mao’s wife, opposed Hua, but Hua had them all arrested on October 6. Deng Xiaoping returned to power in 1977 and launched China’s progress toward becoming a superpower, with greatly increased standards of living for its citizens. One could say that the mandate from heaven had been carried out!
Was the Haicheng prediction a fluke? In August 1976, the month following the Tangshan disaster, the Songpan Earthquake of M 7.2 was successfully predicted by the local State Seismological Bureau. And in May 1995, a large earthquake struck where it was predicted in southwestern China. Both predictions resulted in a great reduction of casualties. As at Haicheng, both earthquakes were preceded by foreshocks.
Why have the Chinese succeeded where the rest of the world has failed? For one thing, Premier Zhou’s call for action led to a national commitment to earthquake research unmatched by any other country. Earthquake studies are concentrated in the China Earthquake Administration (CEA, the new name for the SSB), with a central facility in Beijing, and laboratories in every province. The CEA employs thousands of workers, and seismic networks cover the entire country. Earthquake preparedness and precursor monitoring are carried out at all levels of government, and, in keeping with Chairman Mao’s view that progress rests with “the broad masses of the people,” many of the measurements are made by volunteers, including school children.
Even so, perhaps most and possibly all of the apparent Chinese success is luck. All of the successful forecasts included many foreshocks, and at Haicheng the foreshocks were so insistent that it would have taken a major government effort for the people not to take action and move outdoors on the night of February 4. The Haicheng earthquake was the largest earthquake in an earthquake swarm, whereas the Tangshan earthquake in the following year was a mainshock followed by aftershocks. No major earthquake in recent history in the United States or Japan is known to have been preceded by enough foreshocks to lead to a short-term prediction useful to society. Also, despite the few “successful” predictions in China, many predictions have been false alarms, and the Chinese have not been forthright in publicizing their failures. These false alarms are more than would have been acceptable in a Western country. In addition, the Wenchuan earthquake of M 7.9 in Sichuan Province killed more than 80,000 people. It was not predicted.
6. A Strange Experience in Greece
On a pleasant Saturday morning in May 1995, the townspeople of Kozáni and Grevena in northwestern Greece were rattled by a series of small earthquakes that caused people to rush out of their houses. While everyone was outside enjoying the spring weather, an earthquake of M 6.6 struck, causing more than $500 million in damage, but no one was killed. Just as at Haicheng, the foreshocks alarmed people, and they went outside. The saving of lives was not due to any official warning; the people simply did what they thought would save their lives.
No official warning? Into the breach stepped Panayiotis Varotsos, a solid-state physicist from the University of Athens. For more than fifteen years, Varotsos and his colleagues Kessar Alexopoulos and Konstantine Nomicos have been making earthquake predictions based on electrical signals they have measured in the Earth using a technique called VAN, after the first initials of the last names of its three originators. Varotsos claimed that his group had predicted an earthquake in this part of Greece some days or weeks before the Kozáni-Grevena Earthquake, and after the earthquake he took credit for a successful prediction. Varotsos had sent faxes a month earlier to scientific institutes abroad pointing out signals indicating that an earthquake would occur in this area. But the actual epicenter was well to the north of either of two predicted locations, and the predicted magnitude was much lower than the actual earthquake, off by a factor of 1,000 in energy release.
The VAN prediction methodology has changed over the past two decades. The proponents say they can predict earthquakes of magnitude greater than M 5 one or two months in advance, including a devastating earthquake near Athens in 1999. As a result, Varotsos’ group at Athens received for a time about 40 percent of Greece’s earthquake-related research funds, all without review by his scientific colleagues. His method has been widely publicized in Japan, where the press implied that if the VAN method had been used, the Kobe Earthquake would have been predicted. Although several leading scientists believe that the VAN method is measuring something significant, the predictions are not specific as to time, location, and magnitude. However, VAN has received a lot of publicity in newspapers and magazines, on television, and even in Japanese comic books.
This section on prediction concludes with two quotations from eminent seismologists separated by more than fifty years.
In 1946, the Jesuit seismologist, Father James Macelwane, wrote in the Bulletin of the Seismological Society of America: “The problem of earthquake forecasting [he used the word forecasting as we now use prediction] has been under intensive investigation in California and elsewhere for some forty years, and we seem to be no nearer a solution of the problem than we were in the beginning. In fact the outlook is much less hopeful.”
In 1997 Robert Geller of Tokyo University wrote in Astronomy & Geophysics, the Journal of the Royal Astronomical Society: “The idea that the Earth telegraphs its punches, i.e., that large earthquakes are preceded by observable and identifiable precursors—isn’t backed up by the facts.”
7. Reducing Our Expectations:
Forecasts Rather Than Predictions
Our lack of success in predicting earthquakes has caused earthquake program managers, even in Japan, to cut back on prediction research and focus on earthquake engineering, the effects of earthquakes, and the faults that are the sources of earthquakes. Yet in a more limited way, we can say something about the future; indeed, we must, because land-use planning, building codes, and insurance underwriting depend on it. We do this by adopting the strategy of weather forecasting—20 percent chance of rain tonight, 40 percent tomorrow.
Earthquake forecasting, a more modest approach than earthquake prediction, is more relevant to public policy and our own expectations about what we can tell about future earthquakes. The difference between an earthquake prediction and an earthquake forecast has already been stated: a prediction specifies time, place, and magnitude of a forthcoming earthquake, whereas a forecast is much less specific.
Two types of forecasts are used: deterministic and probabilistic. A deterministic forecast estimates the largest earthquake that is likely on a particular fault or in a given region. A probabilistic forecast deals with the likelihood of an earthquake of a given size striking a particular fault or region within a future time interval of interest to society.
An analogy may be made with hurricanes. The National Weather Service can forecast how likely it is that southern Florida may be struck by a hurricane as large as Hurricane Andrew in the next five years; this is probabilistic. It could also forecast how large a hurricane could possibly be: 200-mile-per-hour winds near the eye of the storm, for example. This is deterministic.
8. The Deterministic Method
The debate in Chapter 4 about “instant of catastrophe” or “decade of terror” on the Cascadia Subduction Zone—whether the next earthquake will be of magnitude 8 or 9—is in part a deterministic discussion. Nothing is said about when such an earthquake will strike, only that such an earthquake of magnitude 9 is possible, or credible. We have estimated the maximum credible (or considered) earthquake, or MCE, on the Cascadia Subduction Zone.
We know the length of the Cascadia Subduction Zone from northern California to Vancouver Island, and, based on slip estimated from other subduction zones worldwide and on our own paleoseismic estimates of the greatest amount of subsidence of coastal marshes during an earthquake (“what has happened can happen”), we can estimate a maximum moment magnitude, assuming that the entire subduction zone ruptures in a single earthquake (Figure 7-2). The moment magnitude of an earthquake rupturing the entire subduction zone at once, with slip estimated from subsidence of marshes, would be about magnitude 9. However, the largest expected earthquake might only rupture only part of the subduction zone with a maximum magnitude of only 8.2 to 8.4. These alternatives are shown in Figure 7-2, remembering that most scientists now favor a MCE of magnitude 9. However, Chris Goldfinger’s work has shown that some earthquakes rupture only the southern part of the subduction zone, as illustrated in the middle and righthand maps in Figure 7-2.
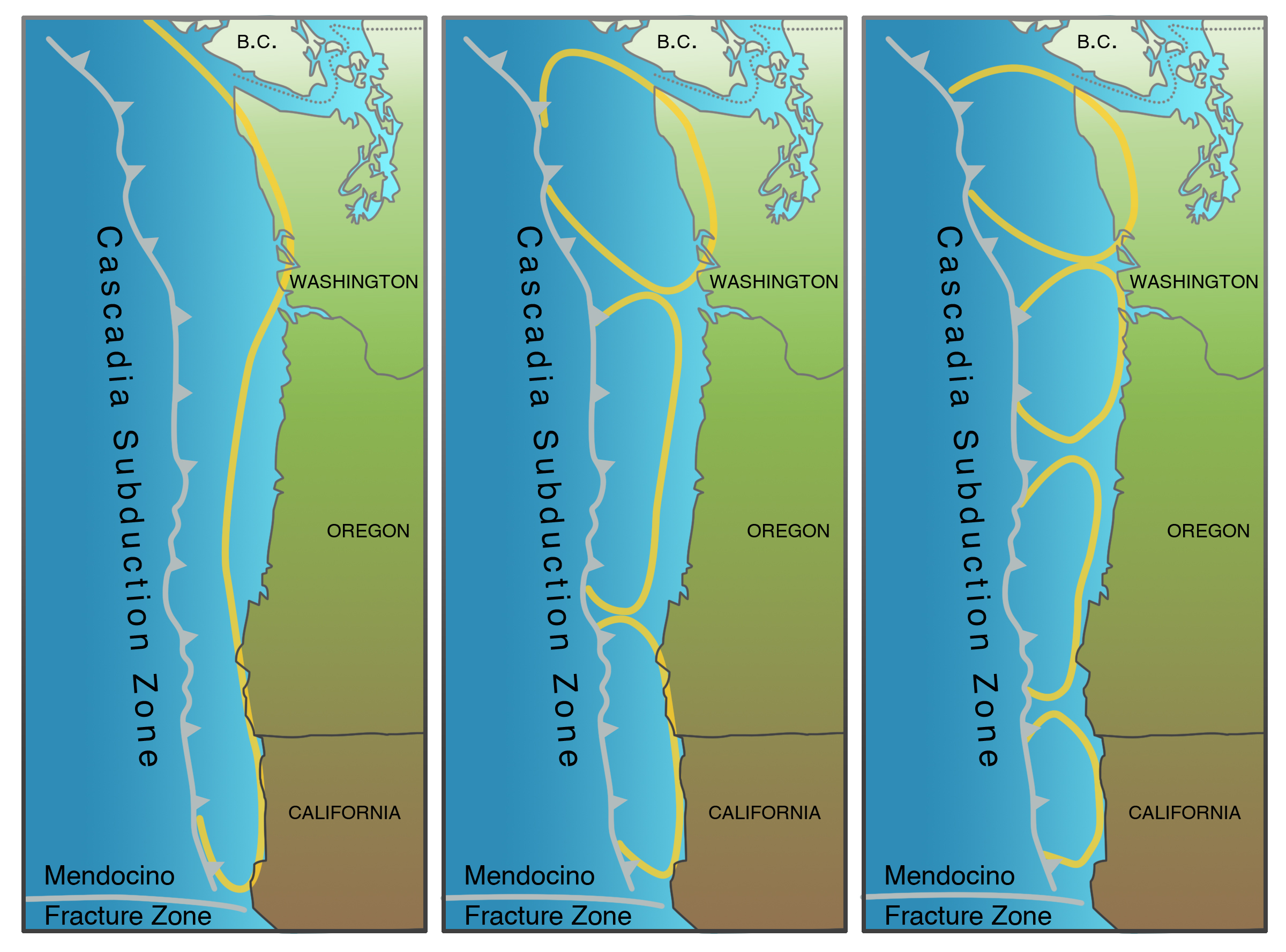
Some probability is built into a deterministic assessment. A nuclear power plant is a critical facility and should be designed for a maximum considered earthquake, even if the recurrence time for it is measured in tens of thousands of years. The result of an earthquake-induced failure of the core reactor would be catastrophic, even if it is very unlikely. The importance of this is illustrated by the failure of the Tokyo Electric Power Company to allow for the possibility of an earthquake as large as M 9 for the Tohoku nuclear power plant and offshore, resulting in nuclear contamination of nearby lands and the Pacific Ocean. Yet there is a limit. The possibility that the Pacific Northwest might be struck by a comet or asteroid, producing a version of nuclear winter and mass extinction of organisms (including ourselves), is real but is so remote, measured in tens of millions of years, that we do not incorporate it into our preparedness planning.
In the Puget Sound region, three deterministic estimates are possible: a magnitude 9 earthquake on the Cascadia Subduction Zone, the MCE on a crustal fault such as the Seattle Fault, and the MCE on the underlying Juan de Fuca Plate, which has produced most of the damage in the region to date. It is difficult to determine the MCE for the Juan de Fuca Plate; scientists guess that the 1949 earthquake of M 7.1 is about as large as a slab earthquake will get. However, the deep oceanic slab beneath Bolivia in South America generated an earthquake greater than M 8, so we really don’t know what the MCE for the Juan de Fuca Plate should be. We will discuss the MCE on the Seattle fault after describing the Gutenberg-Richter relationship.
9. Probabilistic Forecasting
We turn now to probabilistic forecasting. Examples of probability are: (1) the chance of your winning the lottery, (2) the chance of your being struck in a head-on collision on the freeway, or (3) the chance your house will be destroyed by fire. Even though you don’t know if you will win the lottery or have your house burn down, the probability or likelihood of these outcomes is sufficiently well known that lotteries and gambling casinos can operate at a profit. You can buy insurance against a head-on collision or a house fire at a low enough rate that it is within most people’s means, and the insurance company can show a profit (see Chapter 10).
In the probabilistic forecasting of earthquakes, we use geodesy, geology, paleoseismology, and seismicity to consider the likelihood of a large earthquake in a given region or on a particular fault sometime in the future. A time frame of thirty to fifty years is commonly selected, because that is close to the length of a home mortgage and is likely to be within the attention span of political leaders and the general public. A one-year time frame would yield a probability too low to get the attention of the state legislature or the governor, whereas a one-hundred-year time frame, longer than most life spans, might not be taken seriously, even though the probability would be much higher.
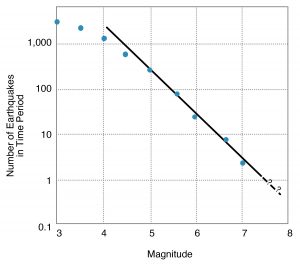
In 1954, Beno Gutenberg and Charles Richter of Caltech studied the instrumental seismicity of different regions around the world and observed a systematic relationship between magnitude and frequency of small- to intermediate-size earthquakes. Earthquakes of a given magnitude interval are about ten times more frequent than those of the next higher magnitude (Figure 7-3). The departure of the curve from a straight line at low magnitudes is explained by the inability of seismographs to measure very small earthquakes. These small events would only be detected when they are close to a seismograph; others that are farther away would be missed. So Gutenberg and Richter figured that if the seismographs could measure all the events, they would fall on the same straight line as the larger events that are sure to be detected, no matter where they occur in the region of interest. Note that Figure 7-3 is logarithmic, meaning that larger units are ten times as large as smaller ones.
This is known as the Gutenberg-Richter (G-R) relationship for a given area. If the curve is a straight line, then only a few years of seismograph records of earthquakes of low magnitude could be extrapolated to forecast how often earthquakes of larger magnitudes not covered by the data set would occur.
A flaw in the assumptions built into the relationship (or, rather, a misuse of the relationship unintended by Gutenberg and Richter) is that the line would continue to be straight for earthquakes much larger than those already measured. For example, if the Gutenberg-Richter curve predicted one M 7 earthquake in ten years for a region, this would imply one M 8 per one hundred years, one M 9 per one thousand years, and one M 10 per ten thousand years! Clearly this cannot be so, because no earthquake larger than M 9.5 is known to have occurred. Clarence Allen of Caltech has pointed out that if a single fault ruptured all the way around the Earth, an impossible assumption, the magnitude of the earthquake would be only 10.6. So the Gutenberg-Richter relationship, used (or misused) in this way, fails us where we need it the most, in forecasting the frequency of the largest earthquakes that are most devastating to society.

Roy Hyndman and his associates at Pacific Geoscience Centre constructed a Gutenberg-Richter curve for crustal earthquakes in the Puget Sound and southern Georgia Strait regions (Figure 7-4). The time period of their analysis is fairly short because only in the past twenty years has it been possible to separate crustal earthquakes from those in the underlying Juan de Fuca Plate. They have reliable data for earthquakes of magnitudes 3.5 to 5 and less reliable data for magnitudes up to about 6.2. The frequency curve means one earthquake of magnitude 3.6 every year and 0.1 earthquake of magnitude 5.1 every year (or one earthquake of that magnitude every ten years). Extending the curve as a straight line would predict one earthquake of magnitude 6 every fifty years.
Hyndman and his colleagues followed modern practice and did not extrapolate the G-R relationship as a straight line to still higher magnitudes. They showed the line curving downward to approach a vertical line, which would be the maximum magnitude, which they estimated as M 7.3 to 7.7. This would lead to an earthquake of magnitude 7 every four hundred years. Other estimates based on the geology lead to a maximum magnitude (MCE) of 7.3, a deterministic estimate. Assuming that most of the GPS-derived -crustal shortening between southern Washington and southern British Columbia takes place by earthquakes, there should be a crustal earthquake in this zone every four hundred years. The last earthquake on the Seattle Fault struck about eleven hundred years ago, but it is assumed that other faults in this region such as the Tacoma Fault or Southern Whidbey Island Fault might make up the difference. Thus geology and tectonic geodesy give estimates comparable to the Gutenberg-Richter estimate for M 7 earthquakes as long as G-R does not follow a straight line for the highest magnitudes.
This analysis works for Puget Sound and the Georgia Strait, where there is a large amount of instrumental seismicity. It assumes that the more earthquakes recorded on seismograms, the greater the likelihood of much larger earthquakes in the future. Suppose your region had more earthquakes of magnitudes below 7 than the curve shown in Figure 7-3. This would imply a larger number of big earthquakes and a greater hazard. At first, this seems logical. If you feel the effects of small earthquakes from time to time, you are more likely to worry about bigger ones.
Yet the instrumental seismicity of the San Andreas Fault leads to exactly the opposite conclusion. Those parts of the San Andreas Fault that ruptured in great earthquakes in 1857 and 1906 are seismically very quiet today. This is illustrated in Figure 7-5, a seismicity map of central California, with the San Francisco Bay Area in its northwest corner. The San Andreas Fault extends from the upper left to the lower right corner of this map. Those parts of the San Andreas Fault that release moderate-size earthquakes frequently, like Parkfield and the area northwest of Parkfield, stand out on the seismicity map. The fault is weakest in this area, and it is unlikely to store enough strain energy to release an earthquake as large as magnitude 7. However, the fault in the northwest corner of the map (part of the 1906 rupture of M 7.9) has relatively low instrumental seismicity, and the fault in the southeast corner (part of the 1857 rupture, also M 7.9) is not marked by earthquakes at all. The segments of the fault with the lowest instrumental seismicity have the potential for the largest earthquake, almost a magnitude 8.

The Cascadia Subduction Zone has essentially zero instrumental seismicity north of California (Figure 4-13). Yet geological evidence and comparisons with other subduction zones provide convincing evidence that Cascadia has ruptured in earthquakes as large as magnitude 9, the last in January 1700.
This shows that the Gutenberg-Richter extrapolation to higher magnitudes works in those areas where there are many small- to moderate-size earthquakes, but not where the fault is completely locked. Seismicity, which measures the release of stored elastic strain energy, depends on the strength of the crust being studied. A relatively weak fault like the San Andreas Fault at Parkfield would have many small earthquakes, because the crust could not store enough strain to release a large one. A strong fault like the San Andreas Fault north of San Francisco would release few or no earthquakes until strain had built up enough to rupture the crust in a very large earthquake, such as the earthquake of April 18, 1906.
Paleoseismology confirms the problems in using the Gutenberg-Richter relationship to predict the frequency of large earthquakes. Dave Schwartz and Kevin Coppersmith, then of Woodward-Clyde Consultants in San Francisco, were able to identify individual earthquakes in backhoe trench excavations of active faults in Utah and California based on fault offset of sedimentary layers in the trenches. They found that fault offsets tend to be about the same for different earthquakes in the same backhoe trench, suggesting that the earthquakes producing the fault offsets tend to be about the same size. This led them to the concept of characteristic earthquakes: a given segment of fault tends to produce the same size earthquake each time it ruptures to the surface. This would allow us to dig backhoe trenches across a suspect fault, determine the slip on the last earthquake rupture (preferably on more than one rupture event), and forecast the size of the next earthquake. When compared with the Gutenberg-Richter curve for the same fault, which is based on instrumental seismicity, the characteristic earthquake might be larger or smaller than the straight-line extrapolation would predict. Furthermore, the Gutenberg-Richter curve cannot be used to extrapolate to earthquake sizes larger than the characteristic earthquake. The characteristic earthquake is as big as it ever gets on that particular fault.
Before we get too impressed with the characteristic earthquake idea, it must be said that where the paleoseismic history of a fault is well known, like that part of the San Andreas Fault that ruptured in 1857, some surface-rupturing earthquakes are larger than others, another way of saying that not all large earthquakes on the San Andreas Fault are characteristic. Similarly, although we agree that the last earthquake on the Cascadia Subduction Zone was a magnitude 9, the evidence from subsided marshes at Willapa Bay, Washington (Figure 4-10a) and from earthquake-generated turbidites (Figure 4-9) suggests that some of the earlier ones may have been smaller or larger than an M 9.
This discussion suggests that no meaningful link may exist between the Gutenberg-Richter relationship for small events and the recurrence and size of large earthquakes. For this relationship to be meaningful, the period of instrumental observation needs to be thousands of years. Unfortunately, seismographs have been running for only a little longer than a century, so that is not yet an option.
Before considering a probabilistic analysis for the San Francisco Bay Area in northern California, it is necessary to introduce theprinciple of uncertainty. There is virtually no uncertainty in the prediction of high and low tides, solar or lunar eclipses, or even the return period of Halley’s Comet. These events are based on well-understood orbits of the Moon, Sun, and other celestial bodies. Unfortunately, the recurrence interval of earthquakes is controlled by many variables, as we learned at Parkfield. The strength of the fault may change from earthquake to earthquake. Other earthquakes may alter the buildup of strain on the fault, as the 1983 Coalinga Earthquake might have done for the forecasted Parkfield Earthquake that did not strike in 1988. Why does one tree in a forest fall today, but its neighbor of the same age and same growth environment takes another hundred years to fall? That is the kind of uncertainty we face with earthquake forecasting.
How do we handle this uncertainty? Figure 7-6 shows a probability curve for the recurrence of the next earthquake in a given area or along a given fault. Time in years advances from left to right, starting at zero at the time of the previous earthquake. The chance of an earthquake at a particular time since the last earthquake increases upward at first. The curve is at its highest at that time we think the earthquake is most likely to happen (the average recurrence interval), and then the curve slopes down to the right. We feel confident that the earthquake will surely have occurred by the time the curve drops to near zero on the right side of the curve.
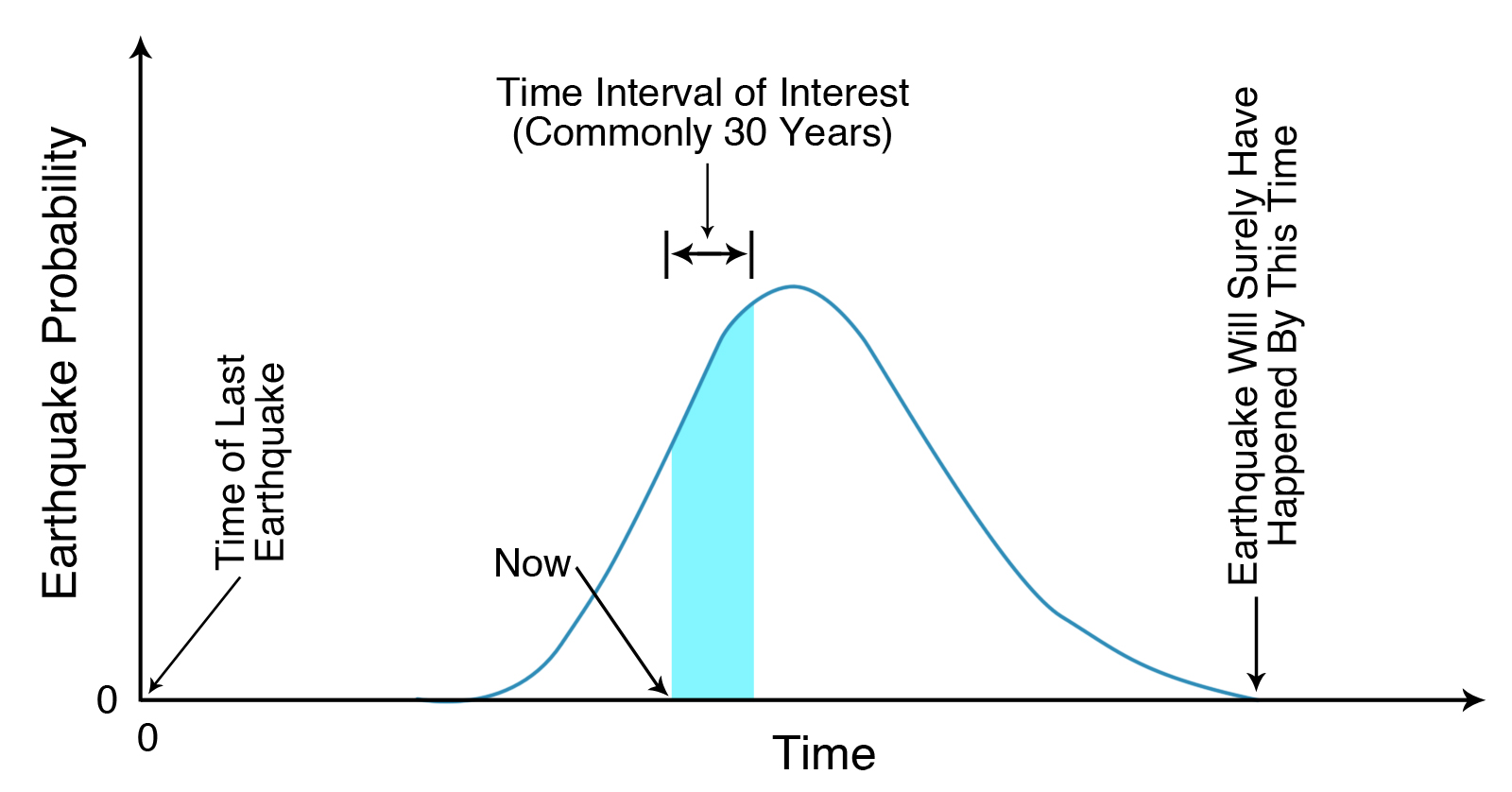
The graph in Figure 7-6 has a darker band, which represents the time frame of interest in our probability forecast. The left side of the dark band is today, and the right side is the end of our time frame, commonly thirty years from now, the duration of most home mortgages. There is a certain likelihood that the earthquake will occur during the time frame we have selected.
This is similar to weather forecasting, except we are talking about a thirty-year forecast rather than a five-day forecast. If the meteorologist on the six-o’clock news says there is a 70 percent chance of rain tomorrow, this also means that there is a 30 percent chance that it will notrain tomorrow. The weather forecaster is often “wrong” in that the less likely outcome actually comes to pass. The earthquake forecaster also has a chance that the less-likely outcome will occur, as was the case for the 1988 Parkfield forecast.
Imagine turning on TV and getting the thirty-year earthquake forecast. The TV seismologist says, “There is a 70 percent chance of an earthquake of magnitude 6.7 or larger in our region in the next thirty years.” People living in the San Francisco Bay Area actually received this forecast in October 1999, covering a thirty-year period beginning in January 2000. That might not affect their vacation plans, but it should affect their building codes and insurance rates. It also means that the San Francisco Bay Area might not have an earthquake of M 6.7 or larger in the next thirty years (Figure 7-7). More about that forecast later.
How do we draw our probability curve? We consider all that we know: the frequency of earthquakes based on historical records and geologic (paleoseismic) evidence, the long-term geologic rate at which a fault moves, and so on. A panel of experts is convened to debate the various lines of evidence and arrive at a consensus, called a logic tree, about probabilities. The debate is often heated, and agreement may not be reached in some cases. We aren’t even sure that the curve in Figure 7-6 is the best way to forecast an earthquake. The process might be more irregular, even chaotic.
Our probability curve has the shape that it does because we know something about when the next earthquake will occur, based on previous earthquake history, fault slip rates, and so on. But suppose that we knew nothing about when the next earthquake would occur; that is to say, our data set had no “memory” of the last earthquake to guide us. The earthquake would be just as likely to strike one year as the next, and the probability “curve” would be a straight horizontal line. This is the same probability that controls your chance of flipping a coin and having it turn up heads: 50 percent. You could then flip the coin and get heads the next five times, but the sixth time, the probability of getting heads would be the same as when you started: 50 percent.
However, our probability curve is shaped like a bell; it “remembers” that there has been an earthquake on the same fault or in the same region previously. We know that another earthquake will occur, but we are unsure about the displacement per event or the long-term slip rate, and nature builds in an additional uncertainty. The broadness of this curve builds in all these uncertainties.
Viewed probabilistically, the Parkfield forecast was not really a failure; the next earthquake is somewhere on the right side of the curve. We are sure that there will be another Parkfield Earthquake, but we don’t know when the right side of the curve will drop down to near zero. Time 0 is 1966, the year of the last Parkfield Earthquake. The left side of the dark band is today. Prior to 1988, when the next Parkfield Earthquake was expected, the high point on the probability curve would have been in 1988. The time represented by the curve above zero would be the longest recurrence interval known for Parkfield, which would be thirty-two years, the time between the 1934 and 1966 earthquakes. That time is long past; the historical sample of earthquake recurrences at Parkfield, although more complete than for most faults, was not long enough. The next Parkfield earthquake actually occurred in 2004, which would have been to the right of the dark band in Figure 6-6 and possibly to the right of the zero line in that figure.
How about the next Cascadia Subduction Zone earthquake? Time 0 is A.D. 1700, when the last earthquake occurred. The left edge of the dark band is today. Let’s take the width of the dark band as thirty years, as we did before. We would still be to the left of the high point in the probability curve. Our average recurrence interval based on paleoseismology is a little more than five hundred years, and it has only been a bit more than three hundred years since the last earthquake. What should be the time when the curve is at zero again? Not five hundred years after 1700 because paleoseismology (Figures 4-9, 4-21) shows that there is great variability in the recurrence interval. The earthquake could strike tomorrow, or it could occur one thousand years after 1700, or A.D. 2700.
10. Earthquakes Triggered By Other Earthquakes:
Do Faults Talk To Each Other?
A probability curve for the Cascadia Subduction Zone or the San Andreas Fault treats these features as individual structures, influenced by neither adjacent faults nor other earthquakes. A 1988 probability forecast for the San Francisco Bay Area treated each fault separately.
But the 1992 Landers Earthquake in the Mojave Desert appears to have been triggered by earlier earthquakes nearby. The Landers Earthquake also triggered earthquakes hundreds of miles away, including an earthquake at the Nevada Test Site north of Las Vegas. The North Anatolian Fault, a San Andreas-type fault in Turkey, was struck by a series of earthquakes starting in 1939 and then continuing westward for the next sixty years, like falling dominoes, culminating in a pair of earthquakes in 1999 at Izmit and Düzce that killed tens of thousands of people.
Ross Stein and his colleagues Bob Simpson and Ruth Harris of the USGS figure that an earthquake on a fault increases stress on some adjacent faults and decreases stress on others. An earthquake temporarily increases the probability of an earthquake on nearby faults because of this increased stress. For example, the Mojave Desert earthquakes might have advanced the time of the next great earthquake on the southern San Andreas Fault by about fourteen years. This segment of the fault has a relatively high probability anyway since it experienced its most recent earthquake around A.D. 1680, but the nearby Mojave Desert earthquakes might have increased the probability even more.
In the same way, a great earthquake can reduce the probability of an earthquake on nearby faults. In the San Francisco Bay Area, the seventy-five year period before the 1906 San Francisco Earthquake was unusually active, with at least fourteen earthquakes with magnitude greater than 6 on the San Andreas and East Bay faults. Two or three earthquakes were greater than M 6.8. But in the next seventy-five years after 1906, this same area experienced only one earthquake greater than M 6. It appears that the 1906 earthquake cast a stress shadow over the entire Bay Area, reducing the number of earthquakes that would have been expected based only on slip rate and the time of the most recent earthquake on individual faults. But the 1989 Loma Prieta Earthquake and 2014 Napa Earthquake might mean that this quiet period is at an end.
However, to keep us humble, the 1989 Loma Prieta Earthquake has not been followed by other large earthquakes on nearby faults. Also, the 1992 Landers Earthquake was followed not by an earthquake on the southern San Andreas fault but by the Hector Mine Earthquake in an area where stress had been expected to be reduced, not raised. Maybe the Landers and Hector Mine earthquakes reduced rather than increased the probability of an earthquake on the southern San Andreas Fault. As in so many other areas of earthquake forecasting, nature turns out to be more complicated than our prediction models. Faults might indeed talk to each other, but we don’t understand their language very well.
11. Forecasting the 1989 Loma Prieta Earthquake:
Close But No Cigar
Harry Reid of Johns Hopkins University started this forecast in 1910. Repeated surveys of benchmarks on both sides of the San Andreas Fault before the great San Francisco Earthquake of 1906 had shown that the crust deformed elastically before the earthquake, and the elastic strain was released during the earthquake. Reid figured that all he had to do was to continue measuring the deformation of survey benchmarks, and when the elastic deformation had reached the stage that the next earthquake would release the same amount of strain as in 1906, the next earthquake would be close at hand.
In 1981, Bill Ellsworth of the USGS built on some ideas developed in Japan and the Soviet Union that considered patterns of instrumental seismicity as clues to an earthquake cycle. A great earthquake (in this case, the 1906 San Francisco Earthquake) was followed by a quiet period, then by an increase in the number of small earthquakes leading to the next big one. Ellsworth and his coworkers concluded that the San Andreas Fault south of San Francisco was not yet ready for another Big One. However, after seventy-five years of quiet after the 1906 earthquake, shocks of M6 to M7 similar to those reported in the nineteenth century could be expected in the next seventy years.
Most forecasts of the 1980s relied on past earthquake history and fault slip rates, and much attention was given to the observation that the southern end of the 1906 rupture, north of the mission village of San Juan Bautista, had moved only two to three feet, much less than in San Francisco or farther north. In 1982, Allan Lindh of the USGS wrote than an earthquake of magnitude greater than 6 could occur at any time on this section of the fault. His predicted site of the future rupture corresponded closely to the actual 1989 rupture, but his magnitude estimate was too low.
In 1985, at a summit meeting in Geneva, General Secretary Mikhail Gorbachev handed President Ronald Reagan a calculation by a team of Soviet scientists that forecast a time of increased probability (TIP)of large earthquakes in a region including central and most of southern California and parts of Nevada. This forecast was based on a sophisticated computer analysis of patterns of seismicity worldwide. In 1988, the head of the Soviet team, V. I. Keilis-Borok, was invited to the National Earthquake Prediction Evaluation Council (NEPEC) to present a modified version of his TIP forecast. He extended the time window of the forecast from the end of 1988 to mid-1992 and restricted the area of the forecast to a more limited region of central and southern California, an area that included the site and date of the future Loma Prieta Earthquake.
Several additional forecasts were presented by scientists of the USGS, including one that indicated that an earthquake on the Loma Prieta segment of the San Andreas Fault was unlikely. These, like earlier forecasts, were based on past earthquake history, geodetic changes, and patterns of seismicity, but none could be rigorously tested.
In early 1988, the Working Group on California Earthquake Probabilities (WGCEP) published a probability estimate of earthquakes on the San Andreas Fault System for the thirty-year period 1988-2018. This estimate was based primarily on the slip rate and earthquake history of individual faults, not on interaction among different faults in the region. It stated that the thirty-year probability of a large earthquake on the southern Santa Cruz Mountains (Loma Prieta) segment of the San Andreas Fault was one in five, with considerable disagreement among working-group members because of uncertainty about fault slip on this segment. The working group forecast the likelihood of a somewhat smaller earthquake (M6.5 to M7) as about one in three, although this forecast was thought to be relatively unreliable. Still, this was the highest probability of a large earthquake on any segment of the fault except for the Parkfield segment, which was due for an earthquake that same year (an earthquake that did not arrive until 2004, when Parkfield was struck by an earthquake of M 6).
Then on June 27, 1988, a M 5 earthquake rattled the Lake Elsman-Lexington Reservoir area near Los Gatos, twenty miles northwest of San Juan Bautista and a few miles north of the northern end of the southern Santa Cruz Mountains segment described by WGCEP as having a relatively high probability for an earthquake. Allan Lindh of USGS told Jim Davis, the California State Geologist, that this was the largest earthquake on this segment of the fault since 1906, raising the possibility that the Lake Elsman Earthquake could be a foreshock. All agreed that the earthquake signaled a higher probability of a larger earthquake, but it was unclear how much the WGCEP probability had been increased by this event. On June 28, the California Office of Emergency Services issued a short-term earthquake advisory to local governments in Santa Clara, Santa Cruz, San Benito, and Monterey counties, the first such earthquake advisory in the history of the San Francisco Bay Area. This short-term advisory expired on July 5.
On August 8, 1989, another M 5 earthquake shook the Lake Elsman area, and another short-term earthquake advisory was issued by the Office of Emergency Services. This advisory expired five days later. Two months after the advisory was called off, the M 6.9 Loma Prieta Earthquake struck the southern Santa Cruz Mountains, including the area of the Lake Elsman earthquakes.
So was the Loma Prieta Earthquake forecasted? The mainshock was deeper than expected, and the rupture had a large component of reverse slip, also unexpected, raising the possibility that the earthquake ruptured a fault other than the San Andreas. Some of the forecasts were close, and as Harry Reid had predicted eighty years before, much of the strain that had accumulated since 1906 was released. Still, the disagreements and uncertainties were large enough that none of the forecasters was confident enough to raise the alarm. It was a learning experience.
12. The 1990 Probability Forecast
The Working Group on California Earthquake Probabilities went back to the drawing boards, and a new probability estimate was issued in 1990, one year after the Loma Prieta Earthquake. Like the earlier estimate, this one was based on the history and slip rate of individual faults, but unlike the earlier estimates, it gave a small amount of weight to interactions among faults. The southern Santa Cruz Mountains segment of the San Andreas Fault, which ruptured in 1989, was assigned a low probability of an earthquake of M greater than 7 in the next thirty years. The North Coast segment of the San Andreas Fault also was given a low probability, even though at the time of the forecast, it had been eighty-four years since the great 1906 earthquake on that segment. The mean recurrence interval on this segment is two to three centuries, and it is still fairly early in its cycle. On the other hand, probabilities on the Rodgers Creek-Hayward Fault in the East Bay Area, including the cities of Oakland and Berkeley, were raised to almost thirty percent in the next thirty years, about one chance in three.
13. The 1999 Bay Area Forecast
The new ideas of earthquake triggering and stress shadows from the 1906 earthquake, together with much new information about the paleoseismic history of Bay Area faults, led to the formation of a new working group of experts from government, academia, and private industry. This group considered all the major faults of the Bay Area, as well as a “floating earthquake” on a fault the group hadn’t yet identified. A summary of fault slip and paleoseismic data was published by the USGS in 1996. A new estimate was released on October 14, 1999, on the USGS web site and as a USGS Fact Sheet.
The new report raises the probability of an earthquake with magnitude greater than M 6.7 in the Bay Area in the next thirty years to 70 percent. Subsequent reviews by the Working Group on California Earthquake Probabilities (WGCEP) have not changed the estimates significantly. Figure 7-7 shows a forecast from 2007 to 2036, and the overall probability of an earthquake of this size or larger on one of the Bay Area faults is 63%. Earthquake probability on the Rodgers Creek Fault and the northern end of the Hayward Fault was given as 31 percent; the probability is somewhat lower on the northern San Andreas Fault, the rest of the Hayward Fault, and the Calaveras Fault. A two-out-of-three chance of a large earthquake is a sobering thought for residents of the Bay Area. These numbers will change in future estimates, but probably not by much.

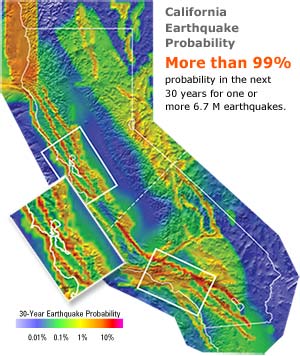
Figure 7-8 is a map showing earthquake probabilities for the entire state of California. The colors on the map are the probability for specific locations over the next thirty years, whereas Figure 7-7 is the probability for specific faults. Note the high probability of an earthquake in the California part of the Cascadia Subduction Zone. Note also that the San Andreas fault and the Hayward-Rodgers Creek fault are shown in bright red, indicating their high probability. The WGCEP estimates that there is more than 99% probability for at least one earthquake of M 6.7 or larger somewhere in California in the next thirty years!
What about the Northwest? Although we know quite a lot about the earthquake history of the Cascadia Subduction Zone, we know too little about the history of crustal faults and almost nothing about faults producing earthquakes in the Juan de Fuca Plate beneath Puget Sound and the Georgia Strait. Chris Goldfinger has estimated the 50-year probability of a Cascadia Subduction Zone earthquake based on the 10,000-year record based on turbidites. He estimates a 10-17 percent chance of a M 9 on the Washington coast and a 15-20 percent chance on the Oregon Coast during this period and a 37% chance of an earthquake of M 8-8,4 during this same period.
In the next chapters, we change our focus from probability of earthquakes of a certain magnitude to probability of strong shaking, which is more important in building codes and designing large structures. Here we have made some progress.
14. “Predicting” an Earthquake After It Happens
Seismic shock waves travel through the Earth’s crust much more slowly than electrical signals. A great earthquake on the Cascadia Subduction Zone will probably begin offshore, up to three hundred miles away from the major population centers of Vancouver, Seattle, and Portland. Seismographs on the coast recording a large earthquake on the subduction zone could transmit the signal electronically to Seattle and Sidney more than a minute before strong ground shaking began. Earthquakes offshore detected using the SOSUS array could give even quicker warning. In addition, Richard Allen, now director of the University of California Berkeley Seismological Lab, and Hiroo Kanamori of Caltech have figured out a way to determine earthquake magnitude with no more than one second of P-wave data. This could give early warning of strong shaking even for slab earthquakes generated thirty to forty miles beneath the ground surface.
This early warning could trigger the shutdown of critical facilities in population centers before the shock wave arrived. Major gas mains could be shut off, schoolchildren could start a duck, cover, and hold drill (see Chapter 15), heavy machinery could be shut down, emergency vehicles could be parked outside, and hospitals could take immediate action in operating rooms. Automatic shutdown systems already exist to stop high-speed trains in Japan. Congress has charged the USGS with the job of submitting a plan to implement a real-time alert system; this is discussed further in Chapter 13. Estimated costs for implementing such a system over five years in the San Francisco Bay Area is $53 million. An alert system is now being developed for the Pacific Northwest (Strauss, 2015).
Additional information on the proposed Advanced National Seismic System, within which this alert system would operate, is available from Benz et al. (2000), USGS (1999), and http://geohazard.cr.usgs.gov/pubs/circ
15. What Lies Ahead
In New Zealand, Vere-Jones et al. (1998) proposed that we combine our probabilistic forecasting based on slip rates and estimated return times of earthquakes with the search for earthquake precursors. Geller (1997) has discounted the possibility that earthquakes telegraph their punches, and up to now, the Americans and Japanese have failed to find a “magic bullet” precursor that gives us a warning reliable enough that society can benefit. Yet precursors, notably earthquake foreshocks, gave advance warnings of earthquakes in China and Greece.
Possible precursors now under investigation include patterns in seismicity (such as foreshocks but in other instances a cessation of small earthquakes), changes in the fluid level of water wells, rapid changes in crustal deformation as measured by permanent GPS stations, anomalous electrical and magnetic signals from the Earth, faults being stressed by adjacent faults that recently ruptured in an earthquake, even the effects of Earth tides. For this method to be successful, massive amounts of data must be analyzed by high-speed computers, so that real-time data can be compared quickly with other past data sets where the outcome is known. A single precursor might not raise an alarm, but several at the same time might lead to an alert. The mistake made by previous scientific predictors, including the Chinese, was to put too much dependence on a single precursor and an unrealistic view of how reliable that precursor would be in predicting time, location, and magnitude of a forthcoming earthquake.
In the future, we could see earthquake warning maps pointing out an increased risk beyond that based on earthquake history, analogous to maps showing weather conditions favorable to tornadoes, hurricanes, or wildfires. The TV seismologist or geologist could become as familiar as the TV meteorologist. If an earthquake warning were issued in this way, the public would be much better prepared than they would be if no warning had been issued, and there would be no panic, no fleeing for the exits. If no earthquake followed, the social impact would not be great, although local residents would surely be grousing about how the earthquake guys couldn’t get it right. But they would be alive to complain.
Although we do not have a regional system in place, the USGS maintains an alert system at Parkfield on the San Andreas Fault and at Mammoth Lakes in the eastern Sierra, where volcanic hazard is present in addition to earthquake hazard. Unusual phenomena at either of these places are evaluated and reported to the public. Pierce County, Washington, has established an alert system for possible mudflows from Mount Rainier (Figure 6-1). The monitoring system for metropolitan Los Angeles and the San Francisco Bay Area is becoming sophisticated enough that anomalous patterns of seismicity or other phenomena would be noticed by scientists and pointed out to the public. Indeed, the Lake Elsman earthquakes of 1988 and 1989, prior to the Loma Prieta earthquake, were reported to the Office of Emergency Services, and alerts were issued. There are plans to extend this capability to cities of the Northwest.
16. Why Do We Bother With All This?
By now, you are probably unimpressed by probabilistic earthquake forecasting techniques. Although probabilistic estimates for well-known structures such as the Cascadia Subduction Zone and the San Andreas Fault are improving, it’s unlikely that we’ll be able to improve probability estimates for faults with low slip rates such as the Seattle and Portland Hills faults, unless we’re more successful with short-term precursors. Yet we continue in our attempts, because insurance underwriters need this kind of statistical information to establish risks and premium rates. Furthermore, government agencies need to know if the long-term chances of an earthquake are high enough to require stricter building codes, thereby increasing the cost of construction. This chapter began with a discussion of earthquake predictionin terms of yes or no, but probabilistic forecasting allows us to quantify the “maybes” and to say something about the uncertainties. Much depends on how useful the most recent forecast for the San Francisco Bay Area is, as well as others for southern California. Will the earthquakes arrive on schedule, or will they be delayed, as the 1988 Parkfield Earthquake was, or will the next earthquake strike in an unexpected place?
Why are we not farther along in scientifically reliable earthquake forecasting? The answer may lie in our appraisal in Chapter 2 of the structural integrity of the Earth’s crust—not well designed, not up to code. Some scientists believe that the Earth’s crust is in a state of critical failure—almost, but not quite, ready to break. In this view, the Earth is not like a strong well-constructed building that one can predict with reasonable certainty will not collapse. The crust is more like a row of old tenements, poorly built in the first place with shoddy workmanship and materials, and now affected by rot and old age. These decrepit structures will probably collapse some day, but which one will collapse first? Will the next one collapse tomorrow or ten years from now? This is the dilemma of the earthquake forecaster.
But society and our own scientific curiosity demand that we try.
Suggestions for Further Reading
Allen, R. W., and H. Kanamori, H. 2003. The potential for earthquake early warning in southern California. Science, v. 300, p. 786-89.
Benz, H., J. Gilson,W. Arabasz, L. Gee, and L. Wald. 2000. Advanced National Seismic System Info Sheet; see also http://geohazard.cr.usgs.gov/pubs/circ
Bolt, B. A. 2004. Earthquakes, 5th edition. New York: W.H. Freeman and Co., 378 p.
Clarke, T. 1996. California fault: searching for the spirit of state along the San Andreas. New York: Ballantyne Books, 417 p.
Crampin, S. 1999. Stress-forecasting earthquakes. Seismological Research Letters, v. 70, p. 291-93. Geller, R. J. 1997. Predictable publicity. Seismological Research Letters, v. 68, p. 477-80.
Harris, R. A. 1998. The Loma Prieta, California, earthquake of October 17, 1989—-forecasts. USGS Professional Paper 1550-B.
Jackson, D.D., Earthquake prediction and forecasting: American Geophysical Union Monograph 150, p. 335-348.
Jackson, D. D., Y. Kagan, and S. Uyeda. 1998. The VAN method of earthquake prediction. EOS, Transactions of the American Geophysical Union, v. 79, p. 573, 579-80. (Jackson and Kagan argue against, Uyeda argues for.)
Jordan, T.H., and Jones, L.M., 2010. Operational earthquake forecasting: Some thoughts on why and how: Seismological Research Letters, v. 81, p. 571-574.
Kanamori, H., E. Hauksson, and T. Heaton. 1997. Real-time seismology and earthquake hazard mitigation. Nature, v. 390, p. 481-84.
Lomnitz, C. 1994. Fundamentals of earthquake prediction. New York: John Wiley & Sons, 326 p.
Ma, Z., Z. Fu, Y. Zhang, C. Wang, G. Zhang, and D. Liu. 1990. Earthquake prediction: Nine major earthquakes in China (1966-1976). Beijing: Seismological Press, and Berlin: Springer-Verlag, 332 p.
Olson, R. S. 1989. The politics of earthquake prediction. Princeton, N.J.: Princeton University Press, 187 p. (Includes a description of the Brady earthquake prediction for Lima, Peru.)
Reiter, L. 1990. Earthquake hazard analysis: Issues and insights. New York: Columbia University Press.
Scholz, C. H. 1997. Whatever happened to earthquake prediction? Geotimes, v. 42, no. 3, p. 16-19. Spence, W., R. B. Herrmann, A. C. Johnston, and G. Reagor. 1993.\
Spence, W., R. B. Herrmann, A. C. Johnston, and G. Reagor. 1993. Response to Iben Browning’s prediction of a 1990 New Madrid, Missouri, earthquake. USGS Circular 1083, 248 p.
Stein, R. S. 2003. Earthquake conversations. Scientific American, v. 288, no. 1, p. 72-79 .
Strauss, J., 2015, Vital seconds: The journey toward earthquake early warning for all: Earth, September/October 2015, p. 70-77, www.earthmagazine.org
Response to Iben Browning’s prediction of a 1990 New Madrid, Missouri, earthquake. USGS Circular 1083, 248 p. Stein, R. S. 2003. Earthquake conversations. Scientific American, v. 288, no. 1, p. 72-79.
Vere-Jones, D., D. Harte, and M. J. Kozuch. 1988. Operational requirements for an earthquake forecasting programme for New Zealand. Bulletin of the New Zealand Society for Earthquake Engineering, v. 31, no. 3, p. 194-205.
Whiteside, L. S. 1998. Earthquake prediction is possible. Seismological Research Letters, v. 69, p. 287-88.
Working Group on California Earthquake Proabilities. 1999. Earthquake probabilities in the San Francisco Bay Region: 2000 to 2030—a summary of findings. USGS Circular 1189 and http://quake.usgs.gov/study/wg99/of99-517/index.html
Yeats, R.S., 2001, Living with Earthquakes in California: A Survivor’s Guide. Oregon State University Press, 406 p.
Youngs, R. R., et al. 2003. A methodology for probabilistic fault displacement hazard analysis (PFDHA). Earthquake Spectra, v. 19, p. 191-219.

