10.3: Waves on the Shore

Most of the waves discussed in the previous section referred to deep water waves in the open ocean. But what happens when these waves move towards shore and encounter shallow water? Remember that in deep water, a wave’s speed depends on its wavelength, but in shallow water wave speed depends on the depth (section 10.1). When waves approach the shore they will “touch bottom” at a depth equal to half of their wavelength; in other words, when the water depth equals the depth of the wave base (Figure \(\PageIndex{1}\)). At this point their behavior will begin to be influenced by the bottom.

When the wave touches the bottom, friction causes the wave to slow down. As one wave slows down, the one behind it catches up to it, thus decreasing the wavelength. However, the wave still contains the same amount of energy, so while the wavelength decreases, the wave height increases. Eventually the wave height exceeds 1/7 of the wavelength, and the wave becomes unstable and forms a breaker. Often breakers will start to curl forwards as they break. This is because the bottom of the wave begins to slow down before the top of the wave, as it is the first part to encounter the seafloor. So the crest of the wave gets “ahead” of the rest of the wave, but has no water underneath it to support it (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\) As waves approach shore they “touch bottom” when the depth equals half of the wavelength, and the wave begins to slow down. As is slows, the wavelength decreases and the wave height increases, until the wave breaks (Steven Earle “Physical Geology”).

There are three main types of breakers: spilling, plunging, and surging. These are related to the steepness of the bottom, and how quickly the wave will slow down and its energy will get dissipated.

• Spilling breakers form on gently sloping or flatter beaches, where the energy of the wave is dissipated gradually. The wave slowly increases in height, then slowly collapses on itself (Figure \(\PageIndex{2}\)). For surfers, these waves provide a longer ride, but they are less exciting.

Figure \(\PageIndex{2}\) A spilling breaker. The gentle slope of the bottom causes the wave height to slowly increase until the wave collapses on itself (left: JR, right: James St. John, [CC-BY-2.0], https://www.flickr.com/photos/jsjgeology/23769708334).

• Plunging breakers form on more steeply-sloped shores, where there is a sudden slowing of the wave and the wave gets higher very quickly. The crest outruns the rest of the wave, curls forwards and breaks with a sudden loss of energy (Figure \(\PageIndex{3}\)). These are the “pipeline” waves that surfers seek out.

Figure \(\PageIndex{3}\) A plunging breaker. The steeper slope causes the wave height to increase more rapidly, with the crest of the wave outrunning the base of the wave, causing it to curl as it breaks (left: JR, right: Andrew Schmidt, Public Domain [CC-0], publicdomainpictures.net).

• Surging breakers form on the steepest shorelines. The wave energy is compressed very suddenly right at the shoreline, and the wave breaks right onto the beach (Figure \(\PageIndex{4}\)). These waves give too short (and potentially painful) a ride for surfers to enjoy.

Figure \(\PageIndex{4}\) A surging breaker. The very steep slope causes the wave height to increase suddenly and break right on the beach (left: JR, right: Tewy, [CC-BY-SA-3.0], via Wikimedia Commons).

Wave Refraction

Swell can be generated anywhere in the ocean and therefore can arrive at a beach from almost any direction. But if you have ever stood at the shore you have probably noticed that the waves usually approach the shore somewhat parallel to the coast. This is due to wave refraction. If a wave front approaches shore at an angle, the end of the wave front closest to shore will touch bottom before the rest of the wave. This will cause that shallower part of the wave to slow down first, while the rest of the wave that is still in deeper water will continue on at its regular speed. As more and more of the wave front encounters shallower water and slows down, the wave font refracts and the waves tend to align themselves nearly parallel to the shoreline (they are refracted towards the region of slower speed). As we will see in section 13.2, the fact that the waves do not arrive perfectly parallel to the beach causes longshore currents and longshore transport that run parallel to the shore.

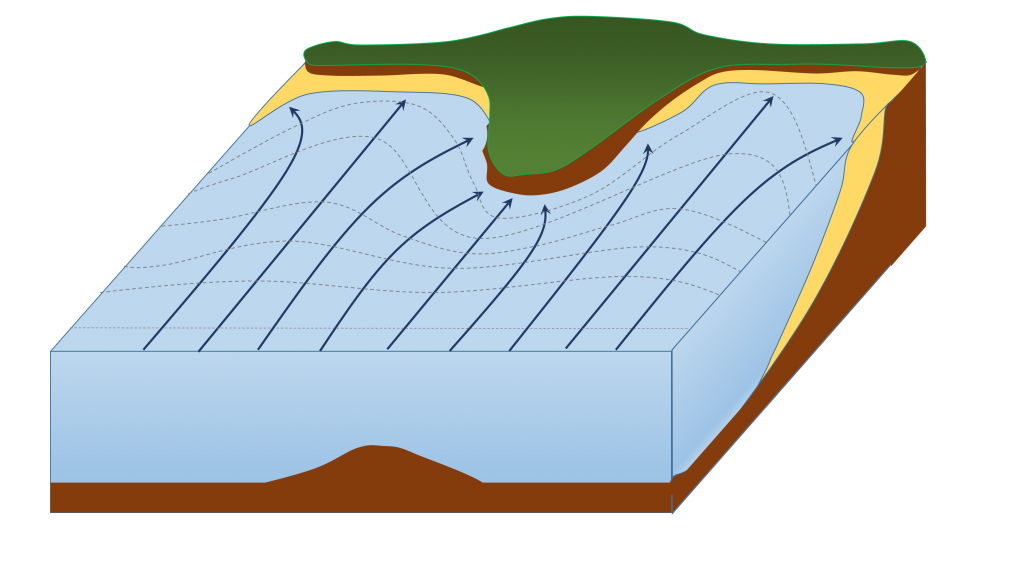
Refraction can also explain why waves tend to be larger off of points and headlands, and smaller in bays. A wave front approaching shore will touch the bottom off of the point before it touches bottom in a bay. Once again, the shallower part of the wave front will slow down, and cause the rest of the wave front to refract towards the slower region (the point). Now all of the initial wave energy is concentrated in a relatively small area off of the point, creating large, high energy waves (Figure \(\PageIndex{6}\)). In the bay, the refraction has caused the wave fronts to refract away from each other, dispersing the wave energy, and leading to calmer water and smaller waves. This makes the large waves of a “point break” ideal for surfing, while water is calmer in a bay, which is where people would launch a boat. This difference in wave energy also explains why there is net erosion on points, while sand and sediments get deposited in bays (see section 13.3).

Figure \(\PageIndex{6}\) Waves approaching shore (blue lines) touch bottom sooner off of points and are refracted towards the points, concentrating their wave energy. Wave energy is spread out in bays, causing smaller waves. Dotted lines represent the bottom contours (PW).