6.10: Why do objects absorb the way that they do?
- Page ID
- 5115
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We see that there is a significant amount of absorption of radiation in the infrared but rather little in the visible. Also, we see that gases absorb strongly at some wavelengths and not at others. Why is this?
To answer this question, we need to look at the configurations of the electrons that are zooming around atoms and molecules. More than 100 year ago, scientists began using prisms to disperse the light from the sun and from flames containing different elements. While the sun gave the colors of the rainbow, the flames had light in very distinct lines or bands. This puzzle was finally resolved a little more than 100 years ago with the invention of quantum mechanics, which basically says that the electrons zooming around atoms and molecules and the vibrations and rotations of molecules can have only discrete energies that are governed by rules of conservation of angular momentum.

The following bulleted list is a crash course in absorption by the electrons in atoms and molecules. Refer to the figure below the box.
Crash Course: Absorption by the Electrons in Atoms and Molecules
- Chemical bonds and quantum mechanics together determine the energy levels that any electron, atom, or molecule can be in.
- The molecular energy is a sum of the energy related to the position of the electron relative to the stable ground electronic state, the molecular vibration, and the molecular rotation.
- Absorption occurs when the energy of the photon matches the difference between two energy levels in a molecule, ΔE = Efinal – Einitial = hc/λ.
- Rules set by conservation of angular momentum and electron spin determine which transitions are allowed.
- The amount of absorption, called simply the absorption cross section, σ, comes from many factors, but varies significantly from molecule to molecule and from transition to transition. The cross section has dimensions of area and commonly has units of cm2.
- Electronic transitions occur when the electrons actually jump into other orbits around the nuclei. They have energies that are equivalent to radiation (i.e., photons) in the ultraviolet to visible wavelengths.
- Vibrational transitions occur when the molecule vibrates at a different frequency or in a different way. Diatomic molecules (e.g., O2 and N2) have only one way to vibrate—back and forth along the chemical bond that binds them. But more complicated molecules (e.g., H2O and CO2) can vibrate not only with the nuclei going toward and away from each other, but also by bending in three directions. These vibrational transitions, accompanied with motions that combine vibration and rotation, have energies equivalent to the near and middle infrared radiation (i.e., photons).
- Rotational transitions occur when a molecule changes its rate of rotation. These transitions have energies equivalent to radiation (i.e., photons) in the far infrared to radio wave wavelengths.
- Translational energies of molecules in Earth's atmosphere, ~kT, are generally a little larger than the energy required to move from one rotational level to another, 10–100 times less than the energy required to go from one vibrational level to another, and hundreds to thousands of times less than what is required to go from one electronic level to another.
- We have already seen that some molecules and atoms have more kinetic energy than others. All molecules with kinetic energy larger than the energy difference between rotational levels can collide with the molecule and give it enough rotational energy to change to a higher rotational level. Thus, we see that rotational energy is distributed over many rotational levels, but that vibrational and electronic levels are usually the ground (lowest energy) levels.
- Atoms do not have molecule-like vibrations and rotations because they have only one nucleus, so their spectra consist only of electronic transitions.
- A sharp transition from one discrete level to another, which appears as a line in a spectrum, occurs in a narrow range of energies about the transition energy difference. The resulting radiation occurs in a narrow band of wavelengths about the line's central wavelength. The width of this line (measured at half the line's maximum height) is called the linewidth.
- This natural linewidth can be broadened by the molecule’s motion, called Doppler broadening, or by collisions, called pressure broadening.
- High in the atmosphere, Doppler broadening is dominant because the pressure is low, but lower in the atmosphere, pressure broadening becomes dominant even though Doppler broadening also increases. So the absorption lines are broader near Earth’s surface than they are higher up in the atmosphere.
The absorption cross section, σ, varies significantly over the width of the absorption line. So it is possible for all the radiation to be absorbed in the middle of the line but very little absorbed in the “wings.”
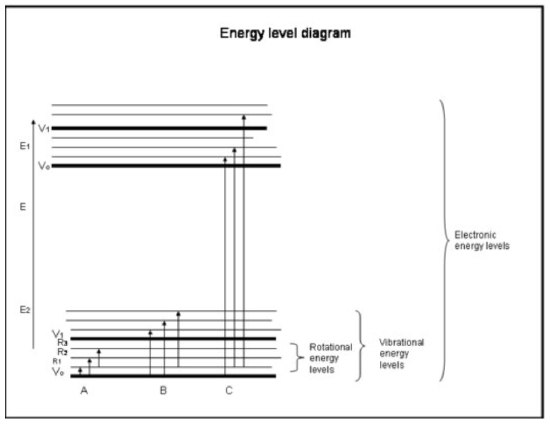
Physical Interpretation
Atoms and molecules can absorb radiation (a photon) only if their structure has an energy difference between levels that matches the photon’s energy (hc/λ). Otherwise, the atom or molecule will not absorb the light. Once the molecule has absorbed the photon, it can either lose a photon and go back to its original lower energy level; or it can break apart if the photon energy is greater than the chemical bond holding the molecule together; or it can collide with other molecules, such as N2 or O2, and transfer energy to them while it goes back to its lower energy level. Collisions happen often, so the energy of the absorbed photon is often transferred to thermal energy.
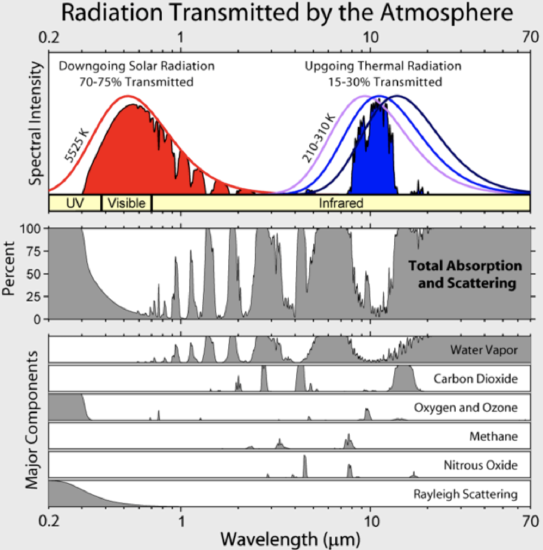
Note that Earth's upgoing infrared irradiance is limited to a few atmospheric "windows" and the irradiance at all other wavelengths is strongly absorbed, mostly by water vapor, but also by carbon dioxide, ozone, nitrous oxide, methane, and other more trace gases that aren't shown in the figure above.

