14.1: Front Matter
- Page ID
- 14845
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)What Is Geologic Time?
The amount of time involved in carving a landscape, forming rocks, moving continents is an important scientific question. Different hypotheses about the age of the Earth offer drastically different perspectives of the workings of geologic events that formed and shaped the planet. For example, if geologic time is relatively short (less than a 100 million years) then catastrophic events would have been required to form the features we see on the surface of Earth; whereas vast amounts of geologic time (more than 100 million years) could have produced the slow, steady rate of change we observe around us today.
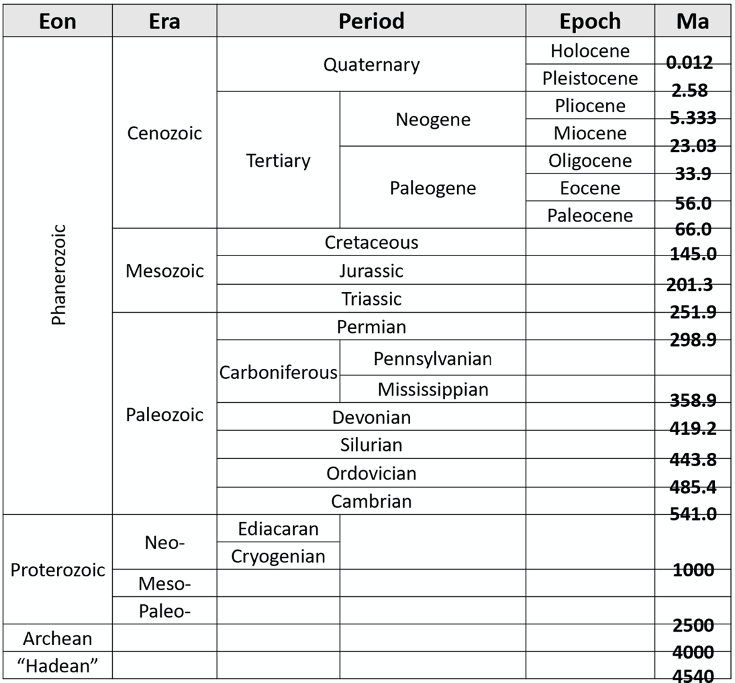
Examining geologic time, or deep time, can be challenging for humans, as it is difficult for us to imagine hundreds of millions or billions of years. Geologists have used a variety of methods to map major geologic events and their duration to reconstruct Earth’s history during the last 4.54 billion years. Early geologists (naturalists) were able to piece together a progression of rocks through time to construct the original Geologic Time Scale, and geologists continue to update and make the timescale more accurate (Figure 14.1). Interested in more GTS? Visit this interactive time scale for more information!
Those who study geologic time can be associated with a variety of disciplines within geology, including sedimentology, paleontology, geomorphology, petrology, structural geology, and many others. Like many other geoscientists, working with other disciplines is common, with a heavy influence from both math and technology. Many are employed by universities where they teach and/or do research, and state and federal agencies, including geological surveys, like the California Geological Survey or United State Geological Survey (USGS). Additional career pathways are available in the private sector including in mining and natural resource extraction. Many of these career options require a college degree and postgraduate work. If you are interested, talk to your geology instructor for advice. We recommend completing as many math and science courses as possible (chemistry is incredibly important for mineralogy). Also, visit National Parks, CA State Parks, museums, gem & mineral shows, or join a local rock and mineral club. Typically, natural history museums will have wonderful displays of rocks, including those from your local region. Here in California, there are a number of large collections, including the San Diego Natural History Museum, Natural History Museum of Los Angeles County, Santa Barbara Museum of Natural History, and Kimball Natural History Museum. Many colleges and universities also have their own collections/museums.
How Do Geologists Measure Geologic Time?
This time scale was constructed by putting in order rock layers that had similar features, such as rock types, environmental indicators, or fossils. Scientists examined clues within the rocks and determined the comparative ages of these layers. This process is called Relative Dating, and helps geologists determine the relative age of one event from another. For example, knowing nothing else about you, I can guess that you are younger than your mother; your actual age doesn’t matter if we can establish from independent evidence that someone, or some event, is older or younger than another.
As time progressed, scientists discovered and developed techniques to date certain rocks, including the age of the Earth itself. Geologists discovered the Earth was billions of years old (4.54 billion years old) and were able to establish a time frame for the Geologic Time Scale. This process is called Numeric or Absolute Dating, which is the process of determining the exact amount of time that has passed since an object was formed or an event occurred.
Both numeric (absolute) and relative dating have advantages and are still frequently used by geologists. Dating rocks using relative dating allows a geologist to reconstruct a series of events quickly, and can be used out in the field on a rocky outcrop. Relative dating also can be used on many different types of rocks, where numeric dating is restricted to certain minerals or materials. However, numeric dating is the only method that allows scientists to place an exact age to a rock.
Relative Time and Geologic Principles
The methods that geologists use to establish relative time scales are based on the Geologic Principles. Before we discuss the different geologic principles, it would be worthwhile to remind ourselves of the different rock types. Sedimentary rocks, like sandstone, are made from broken pieces of other rock that are eroded in higher elevations, transported by wind, water, ice, and gravity to lower areas, and deposited. The cooling and crystallization of molten rock forms igneous rocks. Lastly, the application of heat and pressure to rocks changes them into metamorphic rocks. This distinction is important because these three rock types are formed differently and therefore require different interpretations with respect to dating.
Uniformitarianism
The overarching principle of Uniformitarianism states that the Earth processes we observe today also occurred in the past and over long periods of time. This principle is often summarized as “the present is key to the past”. This principle was originally based on the work of James Hutton and made popular by Charles Lyell in the 19th Century. Uniformitarianism was originally applied only to common, everyday geologic events, and excluded major catastrophic events like an asteroid impact. Many modern geologists will often instead use the term actualism, which examines how the universal physical laws govern both common and catastrophic events (Table 14.1).
| Catastrophism | Uniformitarianism | Actualism | |
|---|---|---|---|
| Type of change | Big, sudden, events | Continuous, uniform, events | Both |
| Rate | Rapid, long ago | Constant | Rates vary; laws do not |
| Description | Begins, usually violently, then changes to something different. | Same events occur over time at same rate; “The present is key to the past” | Universal physical laws are constant; however, Earth may become different if conditions change. |
Original Horizontality
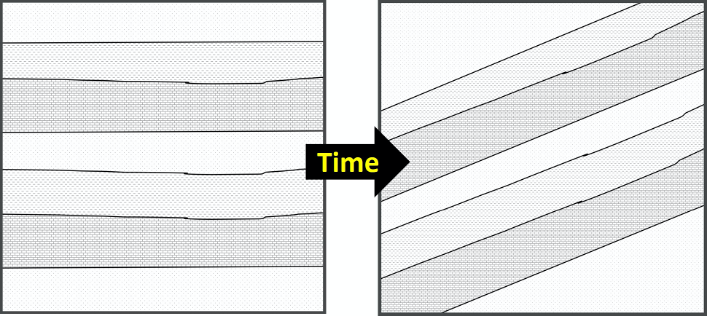
Originally named the “Law of Original Horizontality” by Nicolas Steno in the 17th Century, the Principle of Original Horizontality states that undeformed sedimentary rocks are first deposited horizontally. The deposition of sediment is controlled by gravity and will pull it downward. If you have muddy water on a slope, the water will flow down the slope and pool flat at the base rather than depositing on the slope itself. The implication is that, if a sedimentary rock layer is tilted or folded, it was first deposited flat then folded or tilted after lithification. In other words, sediments are deposited in horizontal layers; only after deposition does deformation occur (Figure 14.2).
Superposition
Originally named the “Law of Superposition” by Nicolas Steno, the Principle of Superposition states that, in an undeformed sequence of sedimentary rocks, the oldest rocks will be at the bottom of the sequence while the youngest will be on top. Imagine a river carrying sand into an ocean: the sand will spill out onto the ocean floor and come to rest on top of the seafloor. This sand was deposited after the sand of the seafloor was already deposited, and is therefore above it. We can envision a relative time scale of rock layers from the oldest rocks at the bottom (#1) to the youngest at the top of an outcrop (#7) (Figure 14.3).
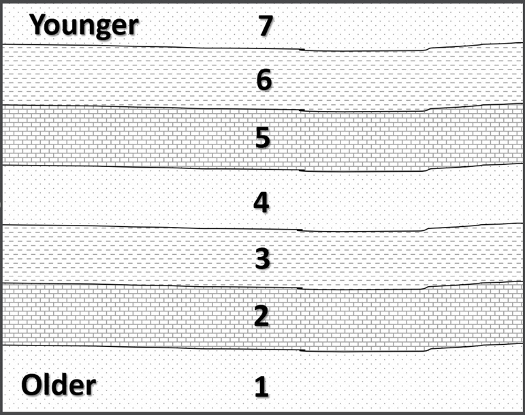
Figure 14.3: The principle of superposition states that in an undisturbed sequence of sedimentary rock, the oldest rocks will be found on the bottom, while the youngest will be located at the top.
Cross-Cutting Relationships
Originally named the “Law of Cross-cutting” by Nicolas Steno, the Principle of Cross-Cutting Relationships states that when two geologic features intersect, the one that cuts across the other is younger, or happened more recently. A feature must be present before something can affect it. For example, if a fault fractures through a series of sedimentary rocks, those rocks had to have existed before the earthquake that formed the fault (Figure 14.4).
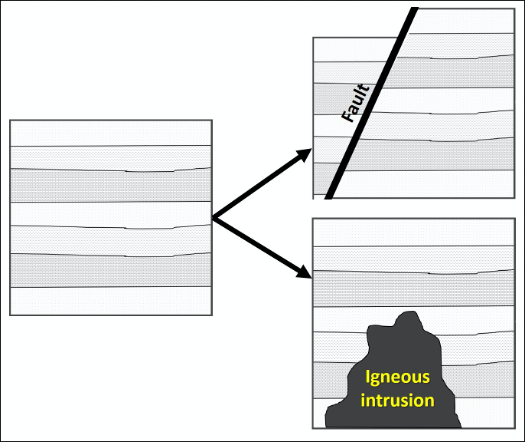
Figure 14.4: Block diagram showing the principle of cross-cutting relationships. The geological features (fault or Igneous intrusion) that cuts across the sedimentary layers must be younger.
Lateral Continuity
Originally named the “Law of Lateral Continuity” by Nicolas Steno, the Principle of Lateral Continuity states that layers of sediment, which lithify to form rock, form laterally extensive horizontal sheets. This means that the same type of sediment will be deposited across a landscape until the environment in which those sediments are deposited ends (e.g. beach sand will be deposited only in a beach environment) or until a physical barrier stops their deposition (e.g. river sediments are structurally confined to river channels). This is useful when correlating layers of rock across a landscape where erosion may have disrupted their continuity (Figure 14.5).
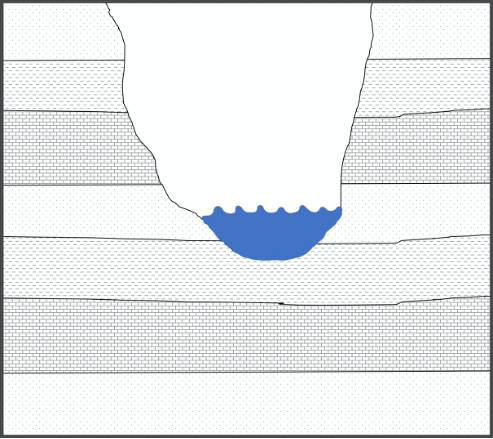
Figure 14.5: The principle of lateral continuity states that layers of sediment form laterally extensive horizontal sheets. The river, which has carved the valley, disrupted the continuity of the layers; however, we can match the rock on either side of the valley using this principle.
Faunal Succession
The Principle of Fossil (Faunal) Succession acts as an independent check to superposition and states that fossils succeed one another in known order. Fossils are the preserved remains of ancient organisms that are normally found within sedimentary rocks. Organisms appear at varying times in geologic history and go extinct at different times. These organisms also change in appearance through time. This pattern of the appearance, change, and extinction of thousands of fossil organisms creates a recognizable pattern of organisms preserved through geologic time. Therefore, rocks of the same age likely contain similar fossils and we can use these fossils to date sedimentary rocks. This principle was discovered by William “Strata” Smith as he worked to survey where the canals could be placed in England.
Certain fossils are particularly useful in telling time; these are called index fossils. These fossils are organisms that were abundant when they were alive, were widespread geographically, have hard parts (shell or skeleton), and have a limited geologic range (the amount of time an organism is alive on Earth). Index fossils are often the quickest and easiest way to date sedimentary rocks precisely and accurately (Figure 14.6).

Inclusions
The Principle of Inclusions states that any rock fragments (inclusions) that are included in a rock must be older than the rock in which they are included. For example, a xenolith in an igneous rock, or a clast in sedimentary rock, must be older than the rock that includes it (Figure 14.7).
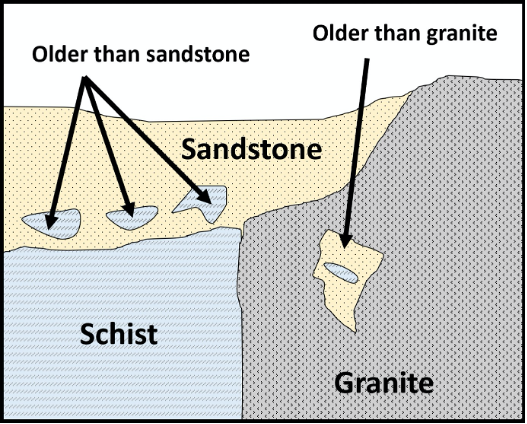
Figure 14.7: Block diagram showing the principle of inclusions, which states that inclusions are always older than the rock they are included within.
Baked Contacts
The Principle of Baked Contacts states that rock encountering molten rock, lava or magma, will become cooked or changed (metamorphosed). The presence of a baked contact indicates the igneous intrusion is younger than the rocks around it. If an intrusive igneous rock is exposed via erosion, then later buried by sediments, the surrounding rocks will not be baked, as the intrusion was already cold at the time of sediment deposition (Figure 14.8).
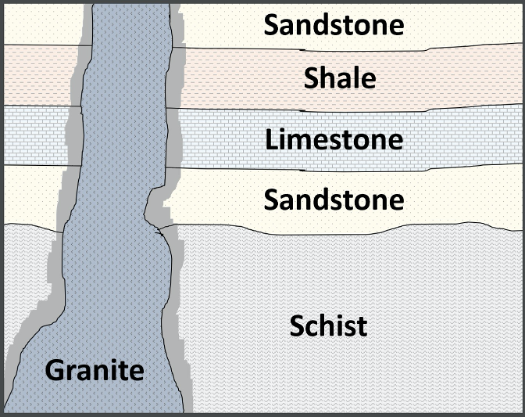
Figure 14.8: Block diagram showing the principle of baked contacts, which states that if a rock encounters a younger igneous event, whether intrusion or lava flow, the rock will become metamorphosed via contact with the younger molten rock.
Unconformities
The history of the Earth is written into strata in much the same way a book is written; occasionally, paragraphs are erased or pages are torn out. In order to fully understand the relative order in which a sequence of rocks formed, we need to know what is missing. Layers of rock or sediments can be described as having a conformable contact or an unconformable contact (unconformity) between them. A conformable contact represents unbroken deposition, with no hiatus (break or interruption in the continuity of the geologic record). The surface strata resulting are called a conformity (Figure 14.9).
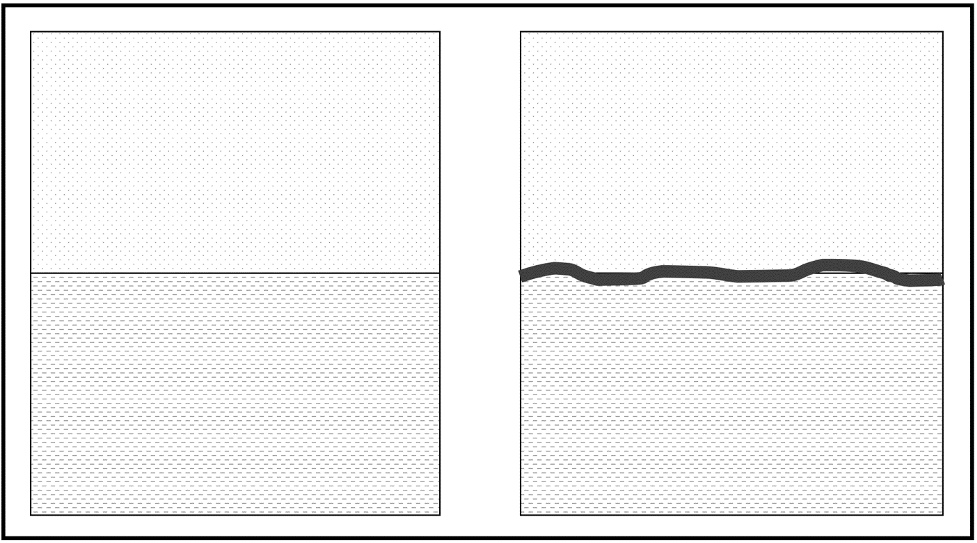
An unconformable contact is a period of erosion or nondeposition. The resulting surface is called an unconformity (Figure 14.9), surfaces between superjacent bodies of rock that reflect missing pages or chapters of Earth history. A sea level fall (regression) may cause sedimentation to cease for a period, or uplift and erosion may remove large volumes of rock from a given region. The amount of time missing can be relatively short or may represent billions of years.
There are three types of unconformities:
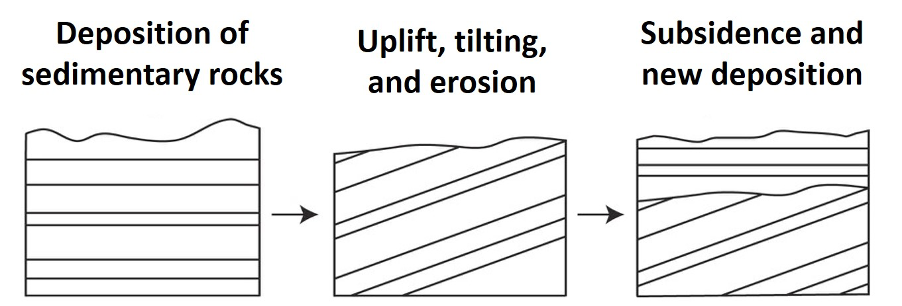
1. An angular unconformity (Figure 14.10) is perhaps the easiest to recognize of the three types of unconformities. Angular unconformities occurs when there is a degree of angular discordance between the layered rocks located above and below the plane of the unconformity. These angles form from tilting, folding, or other forms of deformation related to tectonic processes.
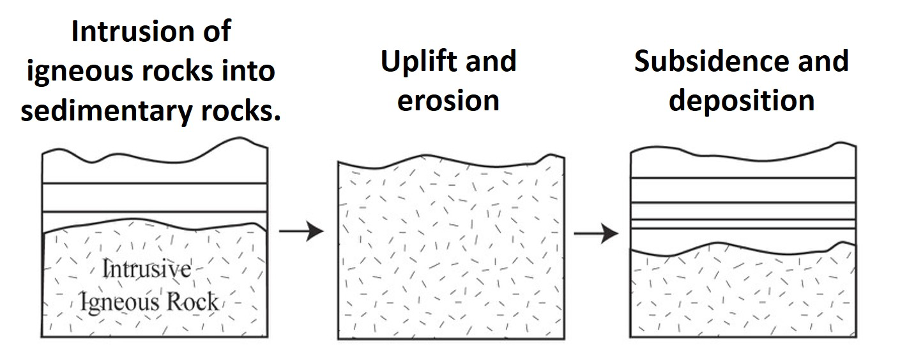
2. A nonconformity (Figure 14.11) is where layered sedimentary rocks overlie an erosion surface developed on metamorphic or igneous rocks. Because the crystalline rocks that underlie nonconformities form deep in the crust were magmatism and regional metamorphism occur, the nonconformity reflects a period of tectonic mountain building followed by a prolonged period of regional erosion. You can remember nonconformities because they form on top of nonlayered rocks.
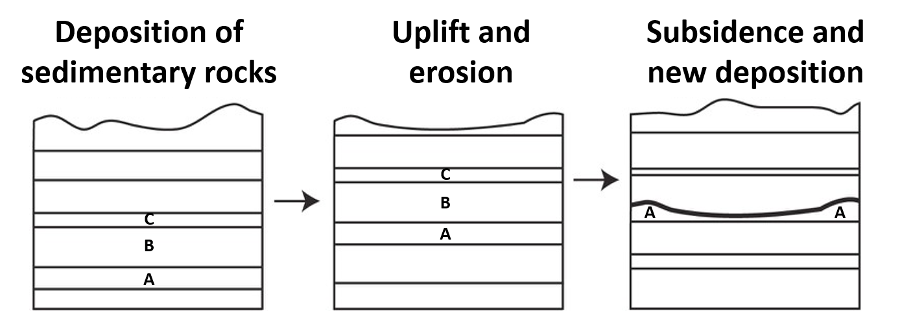
3. A disconformity (Figure 14.12) is a surface of buried erosional relief between parallel layers of sedimentary rock. This makes disconformities more difficult to recognize in the rock record; frequently fossils are needed to determine the exact amount of geologic time missing between layers. Unfortunately, disconformities are fairly common in the rock record, as they frequently form as a result of the natural fluctuations in sea level.
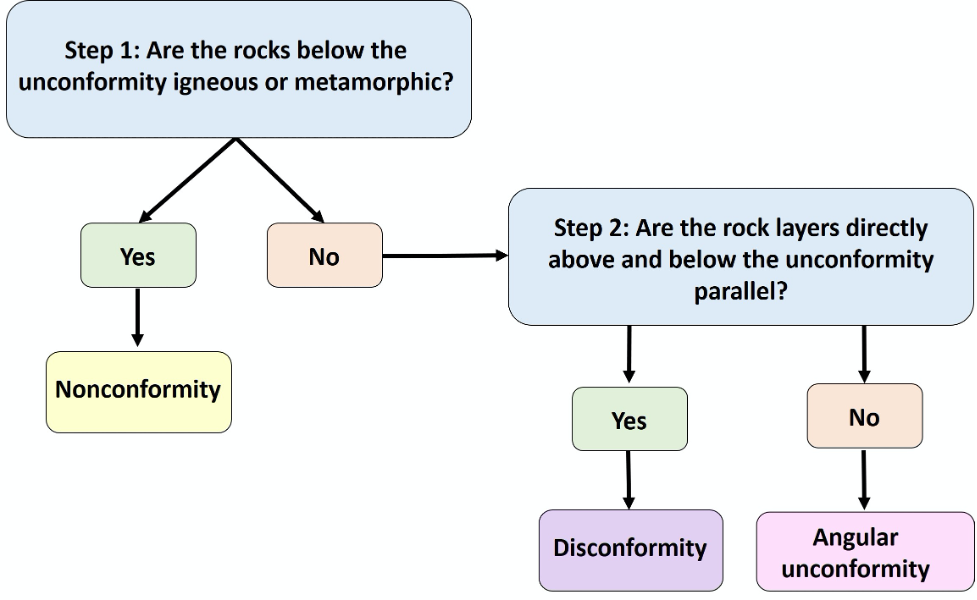
Use this flow chart (Figure 14.13) to determine the unconformity types:
Applying the Geologic Principles to a Geologic History Diagram
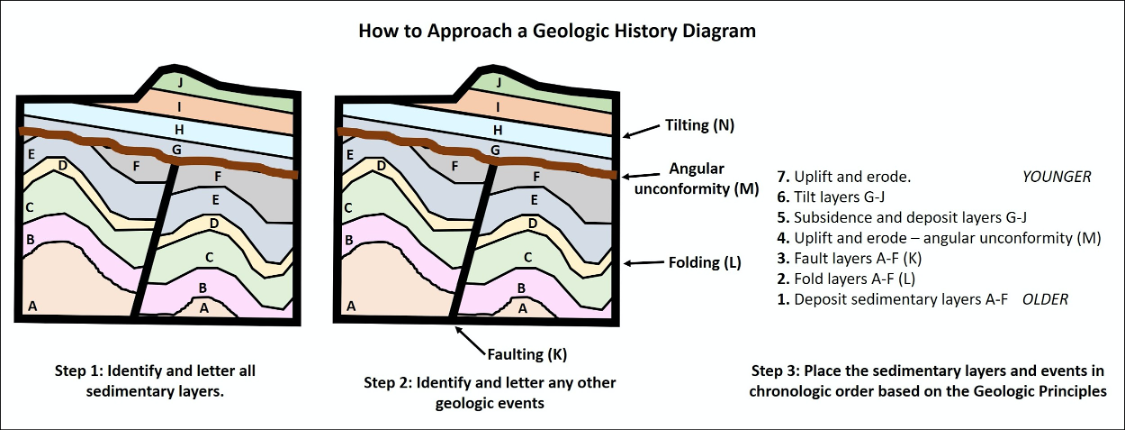
Using these geologic principles, we can examine a series of rock layers and determine their relative ages and establish an order or series of events that must have occurred. Common events that are often recognized can include 1) Deposition of sedimentary layers, 2) Tilting or folding rocks, 3) Uplift and erosion of rocks, 4) Intrusion of liquid magma, and 5) Fracturing or breaking of rock (faulting). Figures 14.14 and 14.15 show how to piece together a series of geologic events using relative dating.

Numeric Dating
Unlike relative dating methods, numeric (or absolute) dating methods provide specific numeric ages for rock layers and help measure the rates at which geologic processes operate. There are numerous scientific techniques to determine a numeric age. For example, we might date trees by counting the number of annual growth rings, using a science called dendrochronology. For geoscientists, however, the most used (and useful!) numeric dating technique is radiometric or isotopic dating. For this technique, radiometric isotopes are measured in rock samples. An isotope is an atom of an element with a different number of neutrons, and therefore different atomic weight; all elements on the periodic table have isotopes. If an atom has too many or too few neutrons in its nucleus, it becomes unstable and breaks down over time, through a process called radioactive decay.

CHEMISTRY THROWBACK: Atoms are made of three particles: protons, electrons, and neutrons. All three of these particles are important to geology. The number of protons defines an element, the number of electrons controls how that element bonds to make compounds, and the number of neutrons changes the atomic weight of an element.
The process of radioactive decay involves the emission of particles from a radioactive isotope – the parent isotope – until it loses enough neutrons, electrons, and protons until it changes into another, more stable, element – the daughter isotope. Scientists can measure the radioactivity of an isotope in the lab and calculate its rate of decay. Though the rate of decay of different isotopes can vary from milliseconds to billions of years, all radiometric isotopes decay in a predictable way.
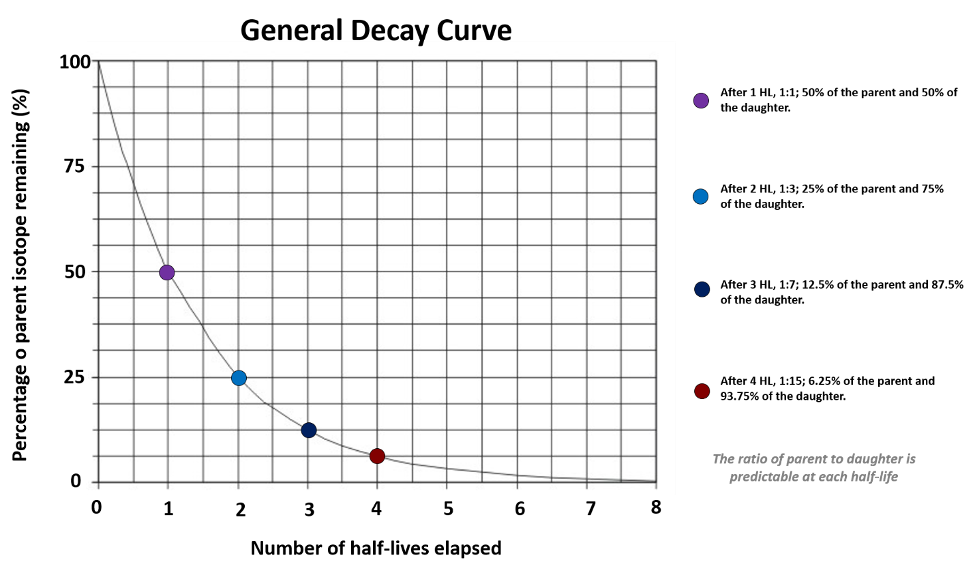
Radiometric decay follows a distinct curve that is defined by a radiometric isotope’s half-life. The half-life is defined as the amount of time it takes for half of the atoms of the radiometric parent isotope to decay to the daughter isotope. The half-life is independent of the number of atoms in a material at a given time; because of this, it takes the same amount of time to go from 100% of the parent isotope remaining to 50%, as it does to go from 50% of the parent isotope remaining to 25% (Figure 14.16).
If the length of the half-life for a radiometric isotope is known, and we measure the amount of parent and daughter isotope in a rock, we can then calculate the age of the rock. Given the shape of the decay curve, a material never runs out of the parent isotope completely; however, after around 10-15 half-lives the amount of the parent isotope left is so small that we are unable to effectively measure it. There are several different radiometric isotopes that are commonly used in numeric (absolute) dating. Each of these systems has different uses within geology, because they require different materials and can date objects within different time frames.
Carbon-14 dating, which may sound familiar to you, is actually of limited use within geology. Carbon-14 (the unstable parent isotope) is found in organic material like bone, tissue, plants, and fiber. This isotope is found naturally in small amounts in the atmosphere within CO2 and is incorporated into plants during photosynthesis and then permeates through the food chain. You currently have carbon-14 in your body that is decaying to nitrogen-14 (daughter isotope), but you replace it whenever you eat. When an animal stops eating or a plant stops photosynthesizing (i.e. when they die), the radioactive carbon starts to decay without being replaced and can be easily measured. Carbon-14 has a very short half-life, only 5730 years, so it can only be used to date materials up to approximately 60,000 years in age. Given that the age of the Earth is 4.54 billion years, carbon-14 is not useful for dating materials from most of Earth’s history.
For geology, we typically require isotopes with much longer half-lives (Table 14.2). Uranium dating involves a complex system of multiple isotopes that decay through a chain reaction until it reaches non-radiogenic lead. Uranium can be found naturally in many igneous rocks, notably the ubiquitous continental rock granite, but in very small amounts. Uranium-238 decays to lead-206, which is also found naturally in many different places; this can make it challenging to differentiate between lead formed from radiometric decay and lead found naturally in the environment.
| Common Half-life Pairs Used in the Geosciences | ||||
|---|---|---|---|---|
| Parent isotope | Daughter isotope | Half-life | Dating range | Comments |
| Potassium-40 | Argon-40 | 1.3 Ga | 10 ka-4.57 Ga | Widely applicable because most rocks have some potassium. Found in Muscovite, Biotite, Hornblende, and whole volcanic rock. |
| Uranium-238 | Lead-206 | 4.5 Ga | 1 Ma-4.57 Ga | The rock must have uranium-bearing minerals. Found in Zircon, and Uraninite. |
| Rubidium-87 | Strontium-87 | 47 Ga | 10 Ma-4.57 Ga | Less precision than other methods at old dates. Found in Muscovite, Biotite, Potassium feldspar, whole igneous or metamorphic rock |
| Carbon-14 | Nitrogen-14 | 5,730 years | 100-60,000 years | Found in wood, charcoal, peat, bone & tissue, shell or other calcium carbonate, groundwater, ocean water, glacier ice. Can be applied to young sediments. |
The mineral zircon (Figure 14.17) solves both issues, by concentrating uranium and excluding lead from its mineral structure. Therefore, we use Uranium dating on zircons found within igneous rocks (such as volcanic ash or rocks formed deep in the earth). Uranium has a very long half-life of 4.57 billion years, which is more than long enough to date most rocks on Earth.
Potassium-Argon dating is also a useful method of dating rocks. Potassium decays into two separate daughter isotopes, argon and calcium. Geologists will measure the amount of argon, a noble gas, in minerals because, unlike calcium, it is rare and does not normally bond with other elements. Therefore, we can be sure that any argon within a mineral is from the decay of potassium. The use of argon also has its drawbacks; for instance, a gas can easily escape from a rock and, therefore, special care needs to be taken in the lab to prevent this. This system works well when there are multiple materials to examine that contain abundant potassium, like the rock granite that is full of the potassium-rich pink feldspars. The half-life of potassium is 1.3 billion years, so, like uranium, it is most useful for dating older rocks.

With all these methods there is still the chance for error such that it is best to think of any particular radiometric date as a scientific hypothesis that needs to be further tested. Typically, numerical dates are reported with a +/- error bar. Error can come from the inclusion or loss of parent or daughter isotopes in the rock following its formation. This can happen for several reasons, most commonly because of heat and pressure (metamorphism). There are ways to correct for these issues that allow scientists to date both the rock and the metamorphic event as long as the geologic history is known. Improvements in technology continue to provide geologists with more precise instrumentation, resulting in more accurate numerical ages. This means every few years a new Geologic Time Scale is produced to accurately reflect ongoing research. This is the most recent timescale available from The Geological Society of America. As you examine the timescale, it might be useful to refer to common unit terminology for isotopic dating (Table 14.3).
| Unit Terminology for Isotopic Dating | ||
|---|---|---|
| Ga | Giga annum | billion years |
| Ma | Mega annum | million years |
| ka | kilo annum | thousand years |
It is improbable to find a rock that contains the exact number of remaining parent isotopes that falls exactly on one of the half-lives. In most cases, we need to use a simple formula to calculate the age of a rock using the length of the half-life and the amount of parent remaining. The formula is:
\[Age = - \left( \frac{t_{\frac{1}{2}}}{0.693} \right) \ln{(p)} \nonumber \]
\(t_{\frac{1}{2}}\) = the length of the half-life in years
\(p\) = the amount of the parent remaining in decimal form. For example, if there is 50% of the parent remaining it would equal 0.5.
Let’s work an example using the above equation; we can be sure we are using the equation correctly because we will already know the answer to in advance. Say you have a sample of bone that has 25% of the Carbon-14 (half-life= 5,730 years) remaining; how old is the sample? We can answer this question in two ways:
- We know that if there is 25% remaining, two half-lives have passed and since each half-life represents 5730 years, the bone would be 11,460 years old.
- We could use the above equation and insert both the length of the half- life and the amount of the parent remaining:
\[Age = - \left( \frac{5730}{0.693} \right) \ln{(0.25)} \nonumber \]
To solve the equation, take the Natural Log (ln) of 0.25 and multiply by the term in the parentheses (make sure to include the negative sign). If you do this, you should get 11,460 years as well.
To visualize this formula, look back at Figure 14.16 which illustrates that all radiometric isotopes decay in a predictable way.
Attributions
- Figure 14.1: “Geologic Time Scale” (CC-BY 4.0; Chloe Branciforte, own work)
- Table 14.1: “Catastrophism, Uniformitarianism and Actualism” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.2: “Original Horizontality” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.3: “Superposition” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.4: “Cross-cutting” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.5: “Lateral Continuity” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.6: Derivative of “Index Fossils” (Public Domain; USGS) by Chloe Branciforte
- Figure 14.7: “Inclusions” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.8: “Baked Contacts” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.9: “Conformable vs. Unconformable” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.10: Derivative of “Unconformities” (CC-BY-SA 3.0; Bradley Deline via LibreText) by Chloe Branciforte
- Figure 14.11: Derivative of “Unconformities” (CC-BY-SA 3.0; Bradley Deline via LibreText) by Chloe Branciforte
- Figure 14.12: Derivative of “Unconformities” (CC-BY-SA 3.0; Bradley Deline via LibreText) by Chloe Branciforte
- Figure 14.13: “Unconformity Flow Chart” (CC-BY 4.0; Chloe Branciforte and Kelli Wakefield, own work)
- Figure 14.14: “How to Approach a Geologic History Diagram #1” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.15: “How to Approach a Geologic History Diagram #2” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.16: Derivative of “Radioactive Decay” (CC-BY-SA 3.0; Kurt Rosenkrantz via Wikimedia Commons) by Chloe Branciforte
- Table 14.2: “Common Half-life Paris Used in the Geosciences” (CC-BY 4.0; Chloe Branciforte, own work)
- Figure 14.17: Derivative of “Zircon Microscope” (CC-BY-SA 3.0; Denniss via Wikipedia) and “M0096D 024 ”(CC-BY-SA 4.0; ManuRoquette via Wikimedia Commons) by Chloe Branciforte
- Table 14.3: “Unit Terminology for Isotopic Dating” (CC-BY 4.0; Chloe Branciforte, own work)


