4.1: Chemistry of Gemstones

An element is a substance that can not be separated into a simpler form of matter by ordinary means. An element may be a solid, liquid or a gas.
Some common elements are carbon, gold, copper, iron, oxygen, silicon, etc.

An atom is the smallest part of an element. It is the smallest, indivisible particle of a chemical element. Each atom consists of negatively charged electrons and positively charged protons. There are a similar number of electrons and protons to produce an electrically neutral atom.

An atom cannot be subdivided by any chemical process.

Basic

Atoms

An atom is the smallest part of an element. It is the smallest, indivisible particle of a chemical element which still possesses all the properties of that element. Each atom consists of negatively charged electrons and positively charged protons as well as uncharged neutrons (with the exception of hydrogen). There are a similar number of electrons and protons to produce an electrically neutral atom.
Protons and neutrons reside in the nucleus while electrons spin around the nucleus in orbitals (not orbits).

Figure \(\PageIndex{1}\): Bohr model of hydrogen (without any neutrons)

Danish physicist Niels Bohr was the first to make a diagram to visualize the components of an atom. The image on the left is such a diagram, drawn to represent a hydrogen atom. Hydrogen is the only atom that does not have a neutron in its nucleus (this is actually only true for the hydrogen isotope protium). It has one positive charged proton in its nucleus and one negative charged electron spinning around the nucleus.
As there are as many positive as negative charges in the atom, the total charge is neutral.

The orbitals around a nucleus are numbered 1 through 7 and serve as energy levels. Formerly they were named K, L, M, N and O shells. One can still use the alphabeticals but the numerical values are preferred.

Every orbital (or energy level or shell) can hold a specific amount of electrons. For n=1 that is 2 electrons and for n=2 that is 8 electrons. One can easily calculate the maximum number of electrons a specific shell can hold by using the formula: 2n².
With n=1, you will get 2 x (1)², or 2 x 1 = 2 electrons.
With n=2, that makes 2 x (2)², or 2 x 4 = 8 electrons etc.

Note

For general gemological purposes, we are not concerned much with protons and neutrons, just electrons (but one should be aware of them).

Electrons fill from the ground up, which means that the lowest shells are filled first before the next shell can get an electron. Electrons tend to travel in pairs and when this happens they are referred to as paired electrons.
In the gallery below, the atom helium has 2 electrons spinning around a nucleus of 2 protons (and 2 neutrons), they fill the first shell completely. Lithium has 3 electrons and since three electrons will fit in the first shell, the third occupies the next level, which is n=2. Beryllium has 4 electrons, thus 2 electrons in n1 (the maximum) and 2 electrons in n2. Finally the 5th element boron has 5 electrons, so 3 electrons travel in n2.

Figure \(\PageIndex{2}\): Helium 2 protons, 2 neutrons and 2 electrons

Figure \(\PageIndex{3}\): Lithium 3 protons, 4 neutrons and 3 electrons

Figure \(\PageIndex{4}\): Beryllium 4 protons, 5 neutrons and 4 electrons

Figure \(\PageIndex{5}\): Boron 5 protons, 6 neutrons and 5 electrons

Molecules

Atoms of elements can combine together to form tiny fractions of new substances known as compounds. A molecule is defined as the smallest fraction of a substance, consisting of two or more elements chemically combined and defining the substance's composition and chemical properties.

Advanced

Atoms and the quantum theory

Figure \(\PageIndex{6}\): Simplified Bohr model with subshells

Although the basic Bohr model with its single energy shells works well most of the time, it cannot be used to understand more complex electron configurations and/or magnetism.
According to the Pauli exclusion principle, no two same particles can be in the same atomic energy state. This brings us to the core of the quantum theory (when electron structure of atoms are described) which relies on 4 quantum numbers:

• The principal quantum number (n)
• The angular momentum quantum number (l)
• The magnetic quantum number (m_l)
• The spin quantum number (m_s)

In the image on the right, a crude example is drawn which shows 4 subshells in the principal shell (n=1). Although it resembles the hydrogen atom, it is only for illustration purposes; not a real situation, as hydrogen has only one subshell (s).

Principal quantum number indicates the energy level of an atom with lower levels having lesser energy and it is expressed in n (also know as the K, L, M, N, O etc shells). There is a maximum of 7 shells and each shell is described as n=1 through n=7.

Angular momentum quantum number (or azimuthal quantum number) can have an integer number of 0 through 3 (although in theory it can go up to 6). These are known as subshells of the energy levels.
Each principal quantum number (or energy level) can have a certain amount of subshells identified by: 0 - (n-1). For hydrogen (with n=1) this will be 0 through 1-1 = only 0. For an atom with n=2 as the highest energy level this will be 0 - 2-1, so 0 an 1. In electron configurations they are named s, p, d, and f according to spectral readings.

These alphabeticals correspond with the subshell numbers:

• 0 = s
• 1 = p
• 2 = d
• 3 = f

Magnetic quantum number has to do with the orientation of the orbital in a magnetic field and takes the integer values -l to +l, so if l=2 (the same as l=d) the magnetic quantum number (m_l) can be -2,-1,0,1 and 2.
These "orbitals" all have the same energy and electrons fill them not in pairs if possible. Only when all are filled with 1 electron the filling goes on until they have paired electrons. These orbitals can hold a maximum of 2 electrons each (Pauli exclusion principle).

Spin quantum number describes how the electrons spin in the energy levels. It can be either 1/2+ or 1/2- (also referred to as upspin and downspin) and one can visualize this as the planet Earth spinning around its axis (clockwise or counter-clockwise).
When two electrons are in the same energy level, one will have upspin and one will have downspin, balancing it to zero.

These spins are what causes magnetism, like in iron for instance. When the energy levels are filled, they fill up with one electron at a time, all having the same spin. When many (unpaired) electrons have the same spin they will act together as a more powerful magnet than when there would only be one unpaired electron (which would be a tiny magnet).

Valency

The valency of an element is determined by the number of its atoms which will combine with, or replace, one atom of hydrogen. It can be observed that some elements will have different valencies in different compounds. For example, the compound FeO (ferrous oxide) is divalent and Fe2O3 (ferric oxide) is trivalent.

Electronic Configuration of Atoms

Properties of an element, chemical compounds and the formation of crystals depend a great deal on the disposition of electrons and their interaction. The electrons circle the nucleus in all directions, like a cloud. The radius of the average of their movements is defined as a shell or energy level. These shells will remain at a predictable level which is determined by quantum mechanics. Each shell contains only a given number of electrons. There is a maximum of 2 in the innermost shell (known as the K shell or n=1), and 8 each in the second shell (known as the L shell or n=2). There are 18 each in the third shell (known as the N shell or n=3) etc following the 2n² rule.

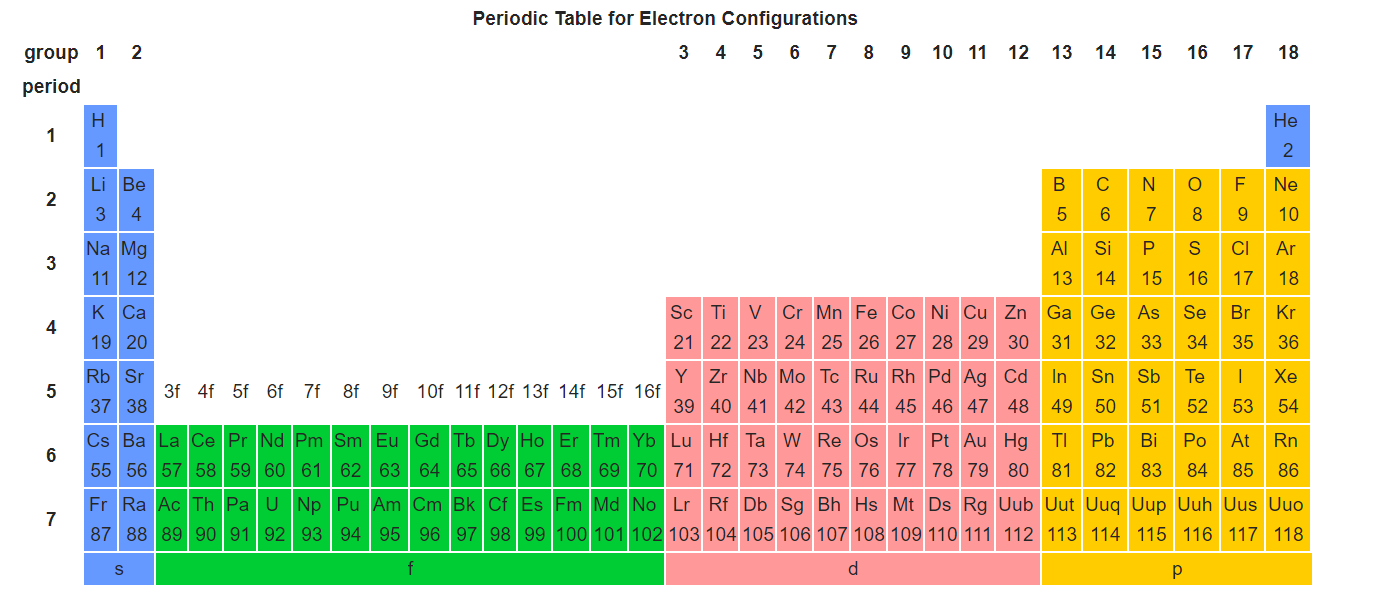
Figure \(\PageIndex{7}\): Periodic Table for Electron Configurations

Atomic Number

Each of the chemical elements is made up of like atoms, also known as the atomic number. They all have the same number of protons. Hydrogen (atomic No. 1), has one proton and one planetary electron. The heaviest naturally occurring atom, uranium, has 92 protons and 92 electrons.
Element 112 was discovered on 9th February 1996 in Darmstadt, Germany. The identified isotope currently is the heaviest atom ever produced by man and has an atomic mass of 277, that is, 277 times heavier than hydrogen.
Except for hydrogen, all the other nuclei of atoms contain neutrons, varying from 2 in the case of helium to 146 in the uranium atom. The atomic weight of an element is the weight of the protons and neutrons, which form the nucleus of the atom. If an atom gains or loses one electron, it ceases to be electrically neutral and becomes what is known as an ion. The gaining of electrons produces a negatively charged ion, known as an anion. Loss of electrons results in a positively charged ion referred to as a cation.

Figure \(\PageIndex{8}\): Mendeljev periodic table of elements