7.9: Glacial Meltwater
- Page ID
- 14341
Glacial Meltwater
General
Glacial meltwater is the liquid water produced by ablation of glaciers. Meltwater is in most glaciers by far the most important product of ablation; it’s much more important than evaporation. Of course, in glaciers that terminate in the ocean, calving is more important.
The importance of glacial meltwater is twofold:
• It’s intimately involved with the movement of glacier ice, by way of its influence on both creep and basal slip.
• Meltwater can carry enormous quantities of glacial sediment and deposit that material nearby or far away from the glacier.
Whereas the activity of the glacier ice itself is greatest near the equilibrium line, the activity of meltwater increases to a maximum at the terminus of the glacier.
Glacial meltwater is abundant on the surfaces of all temperate glaciers below the snowline. Even during the melting season, surface meltwater isn’t common above the snowline, because the water readily sinks into the melting snow. Downglacier of the snowline, however, surface flows of meltwater during the melting season are common. Meltwater is present on polar glaciers only locally and temporarily, because it soon refreezes.
Usually the meltwater streams on the surface of a glacier plunge down into the body of the glacier before they reach the terminus; remember that liquid water is more dense than ice, so the meltwater tries to find a way down into the glacier. It’s a little like pouring water into a pan of semi-connected ice cubes. You know what eventually happens: the ice cubes end up floating in the water. In a real sense, the meltwater of a glacier has a tendency to work its way underneath the glacier so as to cause the glacier to float in its own meltwater. The only thing that keeps a real glacier from becoming like the semi-connected ice cubes floating in your pan is that the balance between production and drainage of meltwater favors drainage over production.
Meltwater is classified on the basis of where it is in the glacier, as supraglacial meltwater (on top of the glacier), englacial meltwater (inside of the glacier), and subglacial meltwater (beneath the glacier). In the same way, the sources of meltwater can be viewed as surficial, internal, and basal. On most glaciers the surface sources are much greater than the internal or basal sources, by one or even two orders of magnitude. Surface sources are strongly seasonal, but internal and basal sources are largely unaffected by the seasons.
Surface sources:
• The main source is ablation during the summer melting season. This drops off sharply upglacier—just the reverse of normal fluvial watersheds.
• Rainfall on the ablation area, mainly in the warm season, is another source. In a narrow technical sense this isn’t meltwater, but it’s indistinguishable from true meltwater and is always considered in the same way.
Internal and basal sources:
• If the ice at the base of the glacier is at its pressure melting point, geothermal heat melts ice there rather than being conducted upward. Depending on the local value of heat flow, this accounts for one or two centimeters of ice thickness per year. Films of meltwater at the bases of glaciers have been observed directly.
• Frictional heating by both internal deformation and basal sliding cause melting if the ice is at its pressure melting point. This generally accounts for something like 0.5 to 5 cm of ice per year.
• Some meltwater is produced by melting by the heat generated by the friction of the meltwater flow itself. The quantities are not important, but this effect seems to be important in creation and maintenance of englacial and subglacial drainageways.
• Groundwater flow out of the regolith and bedrock beneath the glacier is locally important.
Drainage Routes
We observe surface runoff in the form of supraglacial channels, but we also see these surface meltwater streams plunging into crevasses and vertical tubular holes called moulins. And we see important meltwater streams emerging from beneath the glacier at the terminus. So there must be important englacial and subglacial meltwater routes as well as supraglacial routes.
It’s easy to make casual studies of surface meltwater drainage, but there have been few detailed studies. And it’s difficult to study subglacial and especially englacial streams, for obvious reasons. But there are some fairly reliable theoretical approaches that are broadly consistent with what’s known about englacial and subglacial drainage and its depositional consequences.
Surface streams form wherever more meltwater is produced than can be absorbed locally into the glacier or held as pore water in firn or snow at the glacier surface. The stream channels range in size from tiny rills to large channels several meters wide and deep. The streams may or may not be incised into valleys on the glacier surface; that depends on the relative rates of channel downmelting and interchannel ablation.
Meltwater streams on glacier-ice surfaces have a strong tendency to form meanders, much like streams flowing on land. Meandering on ice is no better understood than meandering on sediment, but presumably there’s some kind of instability that involves preferential melting at certain points and less melting, or even refreezing, at other points. In many other cases, however, the courses of the channels are determined by lines of structural weakness in the ice.
Supraglacial streams also tend to form dendritic stream networks, as do stream systems on land. But there are several important differences:
• The network is dense and rill-like; it’s hard to cut major trunk streams when the ice is moving and deforming.
• The drainage pattern shows a strongly subparallel pattern, because of the relatively steep slope of the glacier.
• The drainage density decreases upglacier, because meltwater production decreases upglacier.
• The channel pattern is highly changeable: it looks different each year depending on the development of new englacial drainageways. Remember that the whole glacier surface moves downslope, but the zones of overall extension and compression of the glacier caused by subglacial bedrock topography, which tend to control englacial drainage routes, stay in one place. Moulins develop, are used for several seasons, and then are abandoned as new ones from upglacier take their place.
Dynamics of Meltwater Flow Beneath the Surface
Here are some basic observations on englacial and subglacial meltwater flow:
• In the uppermost zone of the glacier, water flows approximately vertically down crevasses and moulins in free-fall flow. These vertical drainageways have a definite water level in them that can be measured fairly easily. (Try not to fall into one, though.) This water level changes with time, on scales of hours to days, depending on air temperature, sunshine, and rainfall.
• Typically, the changes in water level from moulin to moulin are correlated throughout the entire glacier, suggesting the existence of a connected water table within the glacier.
• This water table can vary from right at the glacier surface, at times of maximum meltwater production in the early part of the melting season, when there aren’t a lot of easily exploitable passageways, to very deep (probably all the way to the base of the glacier) at the end of the melting season, when the passageways are fully developed but the supply of meltwater has dropped off.
• There have been few observations of the shapes of englacial drainageways below the moulins. These drainageways are thought to be nonvertical, with a large horizontal component to their orientation. One piece of evidence: circular englacial tunnels seen in the faces of freshly calved icebergs around the Greenland ice sheet. (A circular tunnel is the equilibrium shape if the water is flowing in a closed conduit in the ice, because approximate isotropy of the polycrystalline ice is usually a good assumption if the ice is far from the base of the glacier, where shearing by internal deformation is strongest.)
• Travel times: dye is injected at points of submergence and monitored where subglacial streams emerge. Speeds of movement are something like 1–2 km per hour, but there’s wide variability. This means total travel times of one to several days on ordinary valley glaciers. But speeds must increase downstream within a given drainage system: the flow in the large ice tunnels at the downstream end of the network is probably very high, many meters per second. The spectacular fountains formed where such subglacial tunnels discharge underwater in glacier-margin lakes is good evidence of this.
• What’s known about flow in large subglacial tunnels? Often the flow emerging from the tunnels has a free surface, but this free surface usually slopes upward relative to the roof in the upstream direction, so it’s reasonable to suppose that only a short distance upglacier the flow is closed-conduit flow, with no free surface. And the streams that terminate beneath glacial lakes are clearly flowing full all the way to the end. At times of low discharge near the end of the melting season, however, most or all of the conduits have free surfaces in them.
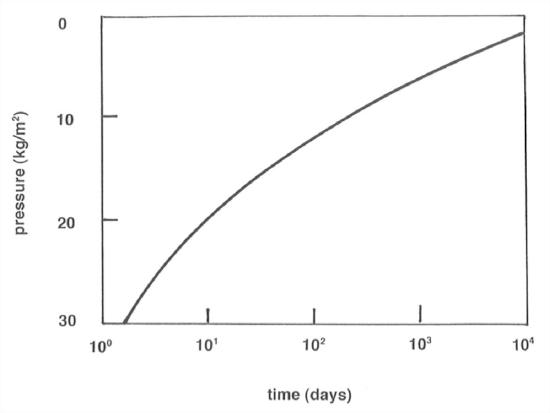
• Any glacial tunnel below a few tens of meters, where ice can flow plastically, tends to close up completely by inflow of ice, if it’s not maintained open by some other means. There are two ways the tunnel can be held open: by water pressure equal to the hydrostatic pressure in the ice itself, or by melting of the walls of the tunnel by the flowing water. Figure 7-27 shows a graph of the half-life time for closing of a vertical ice tunnel as a function of overburden pressure for ice at its pressure melting point.
• Polycrystalline glacier ice at its pressure melting point is known both observationally and theoretically to be permeable to flow of water. There are veins or tiny passageways at three-grain linear boundaries (Figure 5-28), which meet in fours at four-grain point junctions. These junctions have generally tetrahedral shape. This can be observed in careful microscopic work with ice, and it also can be justified in terms of surface-energy arguments. The angle of junction between two ice grains and liquid water is about 20° (Figure 5-29). Water can therefore always percolate through a warm glacier, whatever the state of the large passageways.
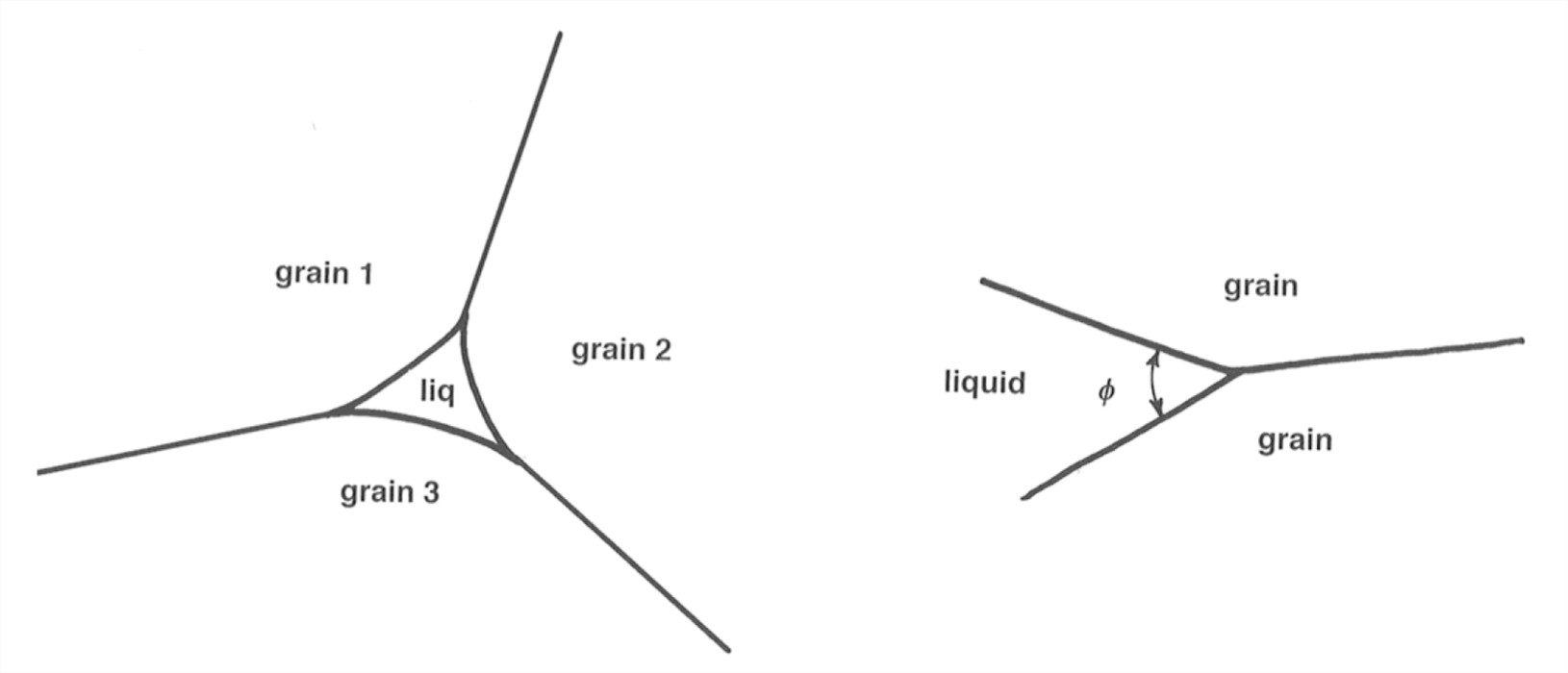
Figure 7-29 (right). The angle of junction between two ice grains and liquid water is about 20°.
The basic idea about the hydraulics of meltwater flow within a glacieristhatthere’safeedbackbetweenwaterpressureandicepressurethat controls the size of the flow tunnels. To understand the nature of these adjustments, look at a simplified tunnel (Figure 7-30) that extends vertically from the surface to the base of the glacier and then horizontally to the terminus. The water table—the free surface of the water in the vertical part of the tunnel—is shown near the surface of the glacier.
If the tunnel is too big, it’s able to carry a greater discharge than is supplied from the glacier surface, and the water level in the vertical tunnel falls. That decreases the water pressure farther along in the tunnel to a value less than the ice pressure around the walls of the tunnel, so the tunnel closes up, thus constricting the flow through the tunnel and causing the water level to rise until the water pressure builds up to be equal to the ice pressure, stabilizing the diameter of the tunnel.
Likewise, if tunnel is too small for a given meltwater discharge, the water table in the vertical part of the tunnel rises, thus increasing the water pressure to a value greater than the ice pressure at the tunnel wall, so the tunnel opens up by radial outflow of the ice wall, leading to increased discharge and a fall in the water table. The tunnel diameter thus again becomes stabilized at a value for which the water pressure is equal to the ice pressure on the tunnel walls.
In accordance with the foregoing argument, it’s usually assumed that in a steady state (constant discharge, certain water level, certain tunnel diameter) the water pressure is equal to the ice pressure at every cross section in the tunnel. But there has to be one significant correction to this. Meltwater discharge through the tunnel tends to melt the tunnel walls, by two effects: (1) the heat generated by friction in the flow, and (2) heat carried from the surface by meltwater that’s slightly above freezing. So at equilibrium the ice walls of the tunnel have to flow inward toward the center of the tunnel at a finite rate to balance this rate of wall melting. The adjustment described above is modified in such a way that the water pressure is a little greater than the ice pressure.
A good case can be made for another important consequence of this wall-melting effect: larger passageways grow at the expense of smaller passageways. The reason? (1) more heat relative to wall area is generated by viscous friction in the larger passageways than in the smaller passageways; and (2) more heat relative to wall area is carried by above-freezing water from the surface in the larger passageways than in the smaller passageways.
The consequence is that because of this differential growth of larger passages, the three-dimensional network of passageways in the glacier tends with time to become dendritic, with tributaries joining into ever-larger trunk passageways. This is broadly consistent with the few observations of the pattern of internal meltwater passageways in glaciers.
ADVANCED TOPIC: THE HYDRAULICS OF MELTWATER FLOW WITHIN GLACIERS
1. The vertical and then horizontal passageway in Figure 7-30 that was usedtoillustratetheforegoingpointsisclearlyunrealistic.What’sthedirectionof meltwater flow in the ice? That question leads in turn to what makes water flow inside a glacier in the first place. The answer to that latter question is: spatial gradients in the difference between the actual water pressure and the hydrostatic pressure (i.e., the pressure that would be measured at the given point if the water were not moving).
2. Figure 7-31 shows this effect in a simplified passageway. The hydrostatic pressure is constant all along the horizontal segment of the passageway, but the water flows from the higher tank to the lower tank because of the gradient in water pressure caused by the difference in water level between the two tanks. If that doesn’t convince you, just consider that the state of flow in the horizontal segment would be exactly the same if you increase the water level in both tanks by the same vertical distance, thereby changing the hydrostatic pressure but not the gradient in pressure.
Figure 7-31. Flow of water in a horizontal passageway due to a gradient in water pressure.
3. Now look at the situation in a real glacier. Think about the water pressure and ice pressure at a point P within the glacier (Figure 7-32). H is the elevation of the ice surface above an arbitrary datum, and z is the elevation of Point P above that same datum. The ice pressure \(p_{i}\)at Point P is
\(p_{i}=\rho _{i}g(H-z)\)(14)
and the water pressure pw at the same point is approximately
\(p_{w}=p_{i}\)(15)
by the line of reasoning in Paragraphs 9.3.2 through 9.3.4. (Forget about the small effect of melting of wall ice.)
Figure 5-32. Definition sketch for analysis of the effect of water pressure and ice pressure at a point in a glacier.
4. Water tends to move through the network of passages in the direction of the gradient of a potential \(\Phi\) that can be represented as a family of smoothly curving surfaces with the property that the direction of most rapid decrease in water pressure is everywhere normal to the surfaces. This is just a generalization of the idea that in a one-dimensional situation like a straight circular pipe the water moves in the direction of decreasing pressure. (It’s just like the gravitational potential function that describes the direction of fall of bodies at all points near the surface of the Earth, which is the direction of most rapid increase or decrease of potential energy as you move the body up or down in the gravity field of the Earth.)
5. The potential can be represented by a equation like
\(\Phi =\Phi _{o}+p_{w}+\rho _{w}gz\)(16)
where the first term on the right is just an arbitrary additive constant, the second term is the actual water pressure, and the third term is the hydrostatic pressure that would be produced by a column of motionless water above the given point.
6. Substituting Equations 14 and 15 into Equation 16 to get rid of pw and pi, and ignoring the arbitrary constant \(\Phi _{o}\),
\(\Phi =p_{i}+\rho _{w}gz
= \rho _{i}g(H-z)+\rho _{w}gz
=\rho _{i}gH+(\rho _{w}-\rho _{i})gz\)(17)
(Remember that the direction of drainage will be normal to the equipotential surfaces.)
7. The dip angle \(\alpha \) of these equipotential surfaces can be found with the aid of Figure 5-33:
\(tan\alpha =\frac{\frac{\partial \Phi }{\partial x}}{\frac{\partial \Phi }{\partial z}}\)(18)
or, solving for the angle
\(\alpha =arctan\frac{\frac{\partial \Phi }{\Phi x}}{\frac{\partial \Phi }{\partial z}}\)(19)
Given that \(\rho _{i}=0.9\rho_{w}\), the result in Equation 19 tells us that englacial tunnels slope downglacier about 11 times as steep as the glacier surface!
8. Then what happens when the passageways reach the base of the glacier? Subglacial tunnels are constrained to follow the locus of steepest descent of the component of the potential function \(\Phi\) parallel locally to the glacier bed. (Just think in terms of the curves lying on the glacier bed that are formed by the intersections of the equipotential surface with the bed, and then taking directions on the bed that are normal to those intersection curves.) On a horizontal glacier bed, this is in the same direction as the surface slope. But if the glacier bed isn’t level, the tunnels can cross bedrock divides. There can even be subglacial lakes, where there are “hollows” in the equipotential surfaces (i.e., where the directions normal to the equipotential surfaces dip locally at a gentler angle than the bed of the glacier).