7.6: Movement of Glaciers
- Page ID
- 14338
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Movement of Glaciers
General Aspects of Glacier Movement
An important consequence of the balance considerations in the previous section is the glacier tends to thicken in its upper part and thin in its lower part, thus increasing its surface slope. The glacier flows under its own weight, passing ice across the equilibrium line to maintain an equilibrium slope. Figure 7-10 is a highly schematic view of how the glacier does this. Figure 7-11, a streamwise vertical cross section through a representative valley glacier, is a less idealized way of looking at this.
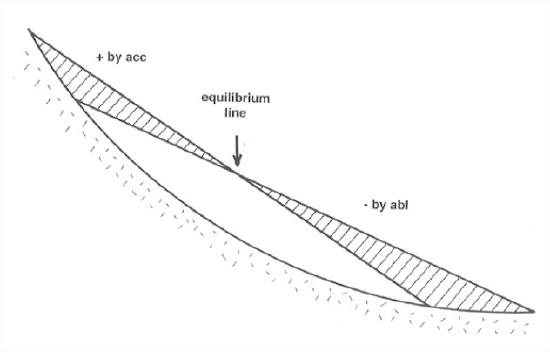

The discharge (volume rate of flow) of a glacier is greatest at the snowline. Why? Because if the profile is to stay the same, the annual discharge through any cross section equals the integral of accumulation minus ablation over the whole area of the glacier above that cross section, and it’s at the equilibrium line that this integral is greatest, because upglacier of the equilibrium line, where the accumulation curve and the ablation curve intersect, the accumulation curve is everywhere above the ablation curve; see Figure 7-5. Does glacier flow fastest there too? Maybe or maybe not; it depends on how the thickness of the glacier varies in longitudinal profile.
Figure 7-12, similar to Figure 7-10, shows a vertical cross section through an ice sheet. In a typical ice sheet the equilibrium line is near the margins of the glacier, because accumulation is small over a broad area but ablation is concentrated near the margins. Note the increase in near-bottom velocity toward the margin and the very slow movement of ice deep in the center of the glacier. If you want to find the oldest ice, that’s where to look.

Velocity of Glaciers
A glacier doesn’t move fast enough for the motion to be perceptible directly to the eye, although in some cases speeds are up to several tens of meters per day, so you could almost see it moving, if you had just the right observation post where you could get a good view of the contact between the base the glacier and the underlying bedrock. But usually speeds are of the order of meters per week or meters per month.
Surface velocities on a valley glacier can be measured easily by planting a straight row of stakes across the glacier, surveying their positions relative to fixed points on the bedrock walls, and then coming back at a later time to resurvey the positions to see how far the glacier has moved downvalley. (This kind of thing is not nearly as easy for ice sheets and ice caps, though.) The first systematic work of this kind was in the French Alps in the 1840s.
If you looked at the resurveyed positions of the row of stakes, what kinds of profiles would you see? Figure 7-13, a map view, shows what’s generally found: an approximately parabolic or U-shaped velocity distribution. Just as with the free-surface flows we looked at in Chapters 1 and 5, this variation in velocity across the profile is a manifestation of internal shearing deformation.
Figure 7-14 shows that you can resolve the total movement into two components: internal deformation, and basal slip, or basal sliding. Basal slip varies in importance from zero in cold, slow glaciers to large in warm, fast glaciers.
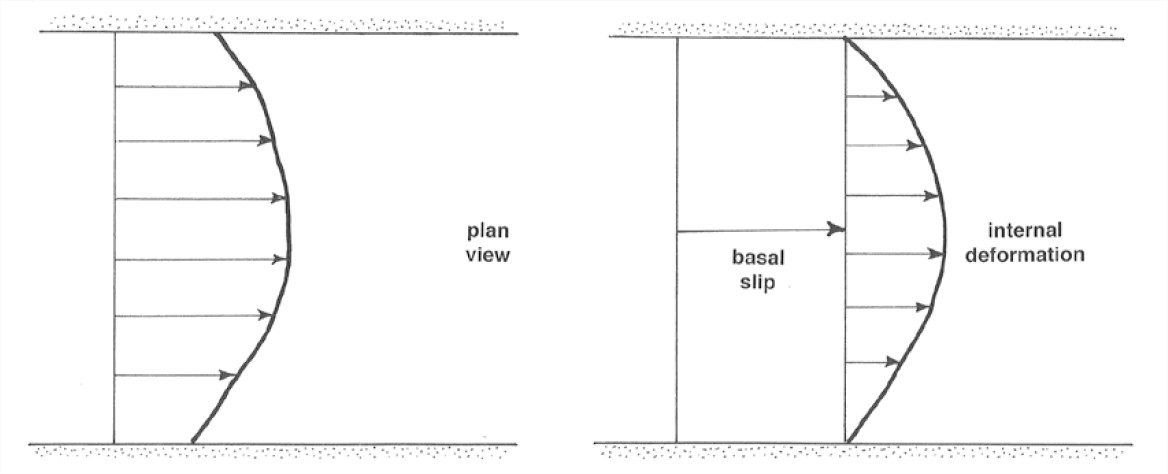
Figure 5-14 (right). Map view of a valley glacier, showing resolution of movement into basal slip and internal deformation.
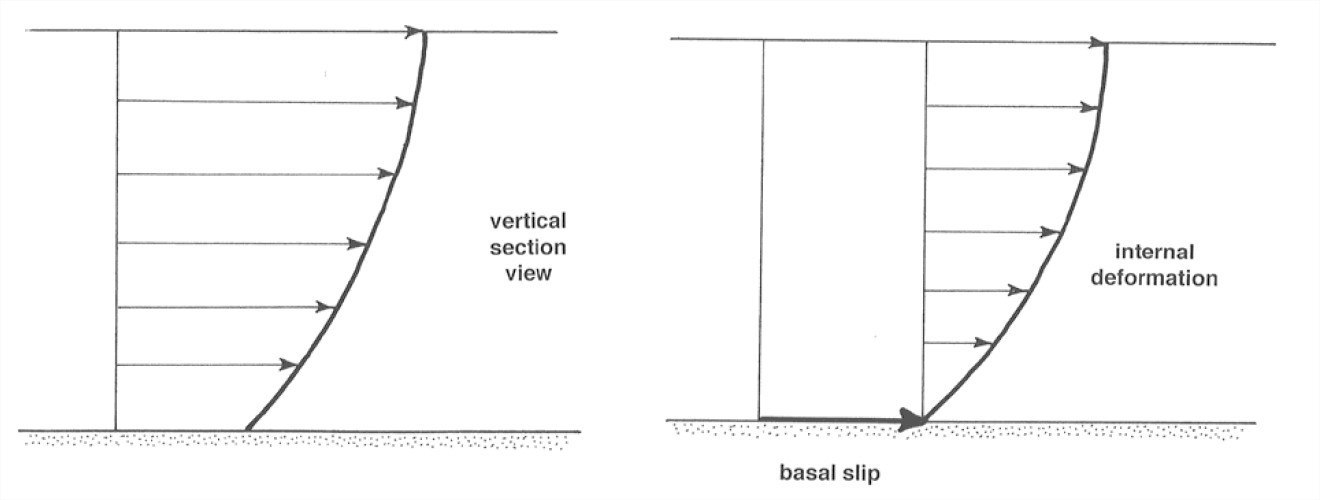
Figure 7-16 (right). Vertical streamwise cross section through a valley glacier, showing resolution of movement into basal slip and internal deformation.
Figures 7-15 and 7-16 show that the picture of velocity distribution is similar in vertical section. Again the motion can be resolved into a component of basal slip and a component of internal deformation.
Figure 7-17 is an example of an unusually complete result on the velocity of ice at the glacier surface, relative to bedrock, as a function of streamwise position on a valley glacier.
One other aspect of glacier velocity is important to understand. Because of accumulation in the upper part of the glacier, what is at the glacier surface at a given time is found at some depth below the glacier surface at a later time. The velocity at which some marker object moves downward from the surface is called the submergence velocity. The corresponding velocity of upward movement of the marker toward the glacier surface in the zone of ablation is called the emergence velocity. In glaciers in temperate regions, a typical value of submergence velocity in the accumulation zone is 1 m/yr, and a typical value of emergence velocity in the ablation zone is 3–4 m/yr.
ADVANCED TOPIC: HOW THE SURFACE VELOCITY OF A GLACIER IS MEASURED
1. How is the surface velocity of a glacier actually measured? Basically, by standard surveying techniques—but there’s more to it than meets the eye. In the following discussion, refer to Figure 7-18. Suppose that you implant a vertical stake in the surface of the glacier somewhere in the ablation area. The slope angle of the ice surface in this part of the glacier is α, and the thickness of the glacier, the minimum distance from bedrock to the glacier surface, is H.
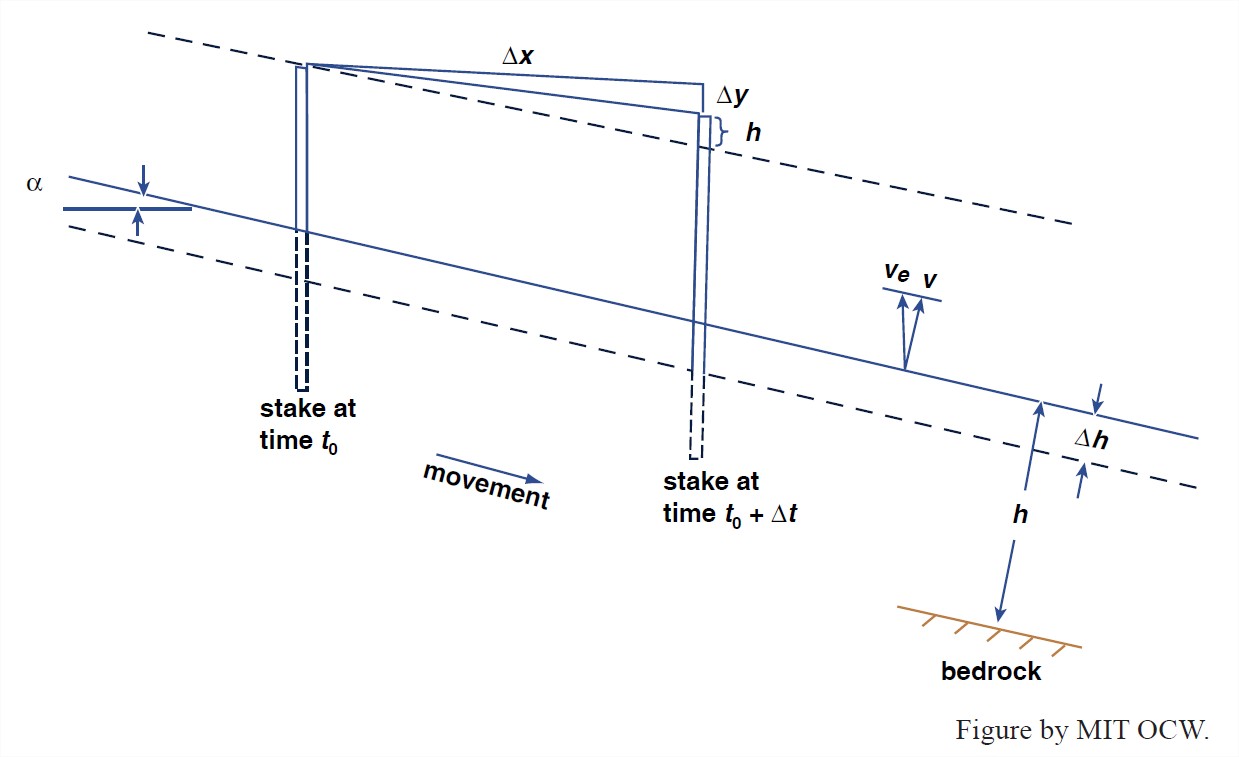
2. Wait a time Δt, while the stake moves some distance down glacier. The horizontal component of movement of the stake, relative to the bedrock beneath the glacier, between time to and time to + Δt is Δx, and the vertical component, again relative to bedrock, is Δy. Clearly the horizontal component of time-average velocity U of the glacier, relative to bedrock, is Δx/Δt. Likewise, the vertical component of velocity, again relative to bedrock, is Δy/Δt. And the resultant velocity of the glacier relative to bedrock is the vector sum of these two velocity components.
3. Note in Figure 7-18 that the ice surface is lowered (or raised) by a distance ΔH normal to the ice surface during time Δt. Think about the net rate of change in ice thickness, ΔH/Δt. Part of ΔH/Δt is accounted for by downward melting of the ice surface, but part is caused by streamwise compression or extension of the whole glacier at this cross section, independently of ablation or accumulation at that point.
4. Let’s deal first with the downward melting of the ice surface. This leads to another interesting vertical velocity: the vertical velocity of the ice relative to the local plane of the glacier ice surface. This is the rate at which the ice surface would rise or fall vertically if there were no ablation or accumulation. It’s this vertical velocity that was called the emergence velocity (in the ablation zone) or the submergence velocity (in the accumulation zone) in Paragraph 6.2.7. It’s so called because if the glacier is at equilibrium with a balanced economy the emergence velocity is how fast things embedded in the ice approach the surface, and the submergence velocity is how fast things put on the ice surface “move away” from the surface to become embedded in the glacier.
5. Shown at the top of the stake at time to + Δt is the distance h, the change in elevation of the top of the stake relative to the plane of the ice surface (not relative to the bedrock beneath the glacier). By use of some trigonometry, the emergence velocity Ve can be written
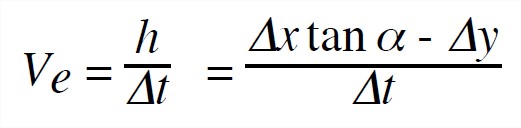 (1)
(1)
6. The component ve of Ve perpendicular to the ice surface is just Ve sin α. This represents the part of the net rate of change of ice thickness H caused by melting; positive ve corresponds to negative ΔH/Δt. The other part of ΔH, remember, is caused by extension or compression; call it vd. The sign of ΔH/Δt is determined by the relative values of ve and vd: in the ablation zone, if vd is negative then ΔH/Δt has to be negative, because positive ve contributes to negative ΔH/Δt. Only if vd is positive and greater in absolute value than ve does the ice surface rise relative to bedrock despite down melting of the ice surface.
6.2.8 So far we’ve talked only about surface velocities. How does one find the velocity of a glacier at depth? It’s a big job. Drill a borehole from the surface to the base of the glacier with a thermal drill, at a speed of something like a meter per hour. This is fairly easy in glacier ice that’s at its melting temperature, but it’s very difficult in glacier ice that’s below its melting temperature. After you finish the hole you have to install a casing, both to keep out melt water and to keep the hole from closing up by deformation!
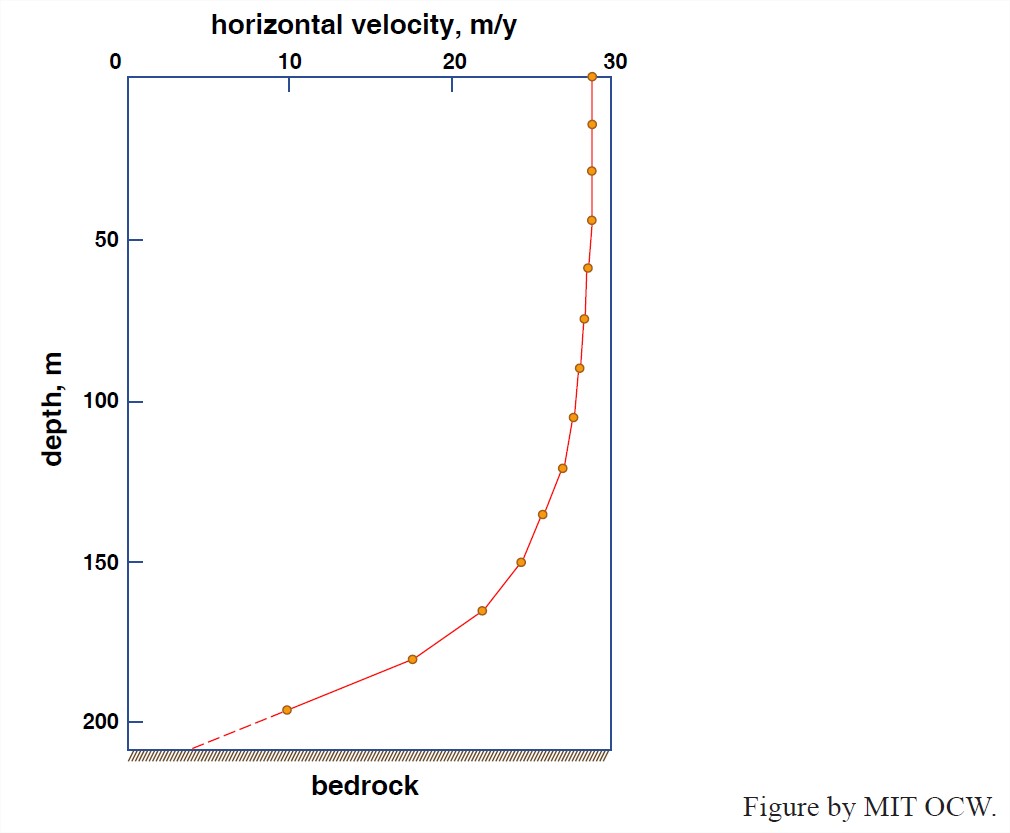
6.2.8 Then put an inclinometer down the hole and read the inclination of the hole as a function of depth; that allows you to plot the vertical profile of the hole (relative to the glacier surface) as a function of time and therefrom find velocities (relative to the glacier surface). This relative-velocity profile is converted to an absolute-velocity profile by combining it with the already- measured absolute surface velocity. But what you cannot determine by this method is the vertical component of velocity at depth. Finally, if your hole reaches bedrock, you can indirectly measure the basal slip. And even if the hole ends a short distance from the base of the glacier, you can get a good idea of the basal slip just by extrapolation. Figure 5-19 shows an example of a vertical velocity profile measured in this way.
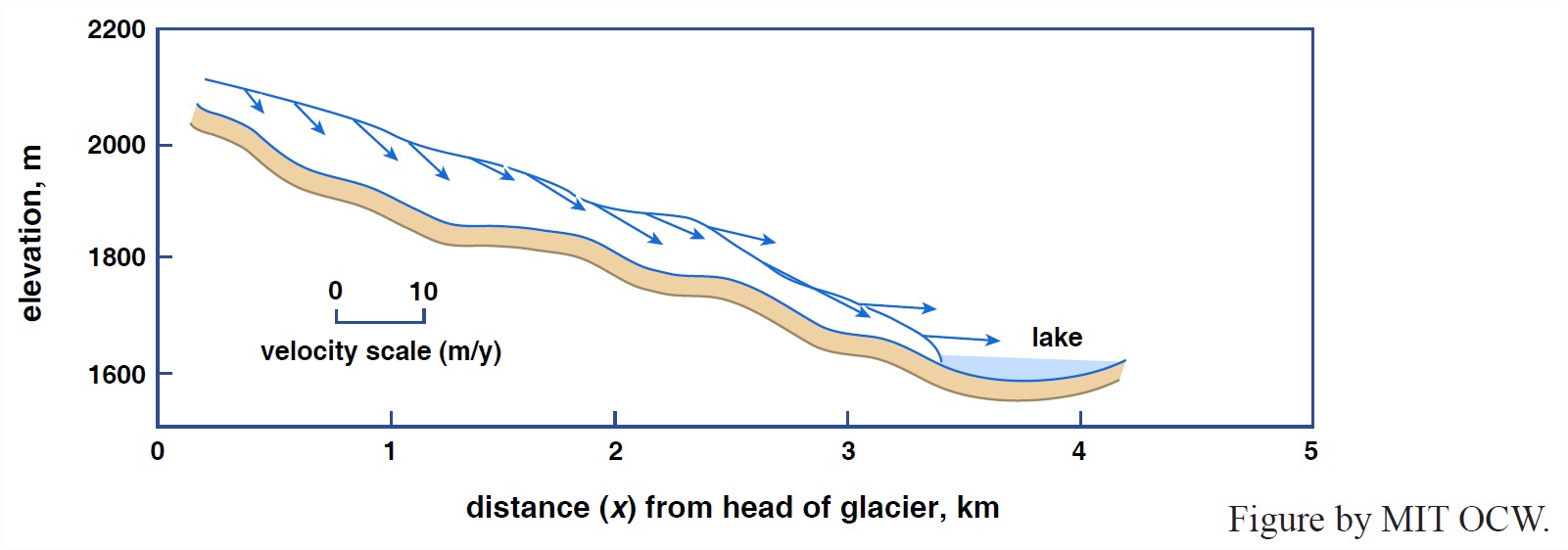
Figure 7-19. Surface velocity vectors from South Cascade Glacier, Washington, U.S., (From Meier and Tangborn, 1965.)

