2.2: Latitude and Longitude

Any point on Earth can be defined by the intersection of its lines of latitude and longitude. Latitude is measured as the angle from the equator, to the Earth’s center, to your position on the Earth’s surface (Figure \(\PageIndex{1}\)). It is expressed as degrees north or south of the equator (0^o), with the poles at a latitude of 90^o. Thus the poles are referred to as high latitude, while the equatorial region is considered low latitude. Lines of equal latitude are always the same distance apart, and so they are called parallels of latitude; they never converge. However, the parallels of latitude do get shorter as they approach the poles.

Figure \(\PageIndex{1}\) The latitude of a point on the Earth’s surface is determined by the angle (ø) between the point and the equator, passing through Earth’s center (Peter Mercator [Public domain], via Wikimedia Commons).

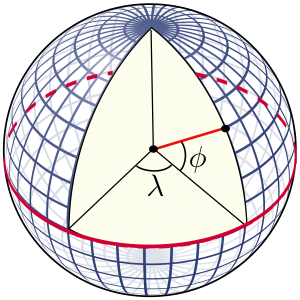
One degree of latitude is divided into 60 minutes (‘). One minute of latitude equals one nautical mile, which is equal to 1.15 land miles (1.85 km). Each minute of latitude is further divided into 60 seconds (“). So traditionally, positions have been expressed as degrees/minutes/seconds, e.g. 36^o 15′ 32″ N. However, with modern digital technology, positions are increasingly expressed as decimals, such as 36^o 15.25 N’, or 36.2597^o N.

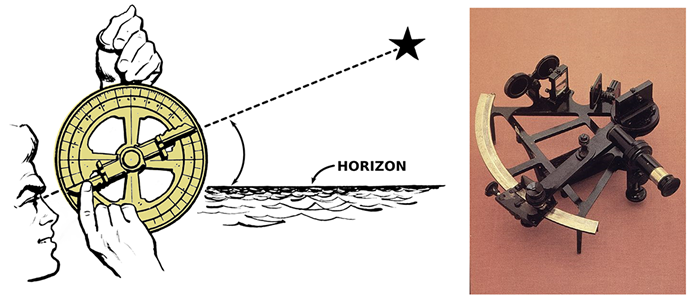
In the Northern Hemisphere, latitude can be determined by the angle of the North Star (Polaris) from the horizon. The North Star always sits over the North Pole. Here, if a person looks straight ahead towards the horizon, the star would be directly overhead, creating a 90^o angle; thus the latitude at the North Pole is 90^o N. At the equator looking north, the star is in the same direction as the horizon, so the angle between them is 0^o, and thus the equatorial latitude is also 0^o. At any other point in the Northern Hemisphere, the angle between the horizon and the star will give the latitude.

Early mariners used an instrument called an astrolabe to calculate this angle. Later the sextant was developed, which allowed more accurate measurements (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\) An astrolabe (left) and sextant (right) (Public domain via Wikimedia Commons).

There is no direct analogue to the North Star in the Southern Hemisphere that is useful for determining latitude. However, the Southern Cross and Centaurus constellations can be used to find the south celestial pole. If a line is drawn through the long axis of the Southern Cross, and another line is drawn between the two brightest stars in Centaurus, the two lines will intersect at the south celestial pole.

Longitude measures the distance east or west of an imaginary reference point, the prime meridian (0^o), which is now defined as the line passing through Greenwich, England (although throughout history the prime meridian has also been located in Rome, Copenhagen, Paris, Philadelphia, the Canary Islands, and Jerusalem; unlike the equator, the prime meridian’s location is fairly arbitrary ). Your longitude represents the angle east or west between your location, the center of the Earth, and the prime meridian (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\) Longitude is determined as the angle (λ) between the prime meridian and your position (Peter Mercator [Public domain], via Wikimedia Commons).

As you move east and west from the prime meridian, eventually you reach 180^o E and W on the opposite side of the globe from Greenwich. This point is the International Date Line. Lines of longitude are called meridians of longitude, or great circles. All circles of longitude are the same length, and are not parallel like lines of latitude; they converge as they near the poles. Therefore, while one minute of latitude always equals one nautical mile, the length of one minute of longitude will decline from the equator to to poles, where it will ultimately decline to zero.

Measuring longitude requires accurate time at your current location, and also the time at some distant point like a home port at the same instant. The time difference can be used to calculate longitude. This is because the Earth takes 24 hours for a complete 360^o rotation. So in one hour, the Earth rotates through 1/24 of 360^o, or 15^o. Therefore, for each hour of time difference between two locations, there is a 15^o difference in longitude.

Accurate measurements of latitude using the North Star have been made since at least the third century B.C.E. Because longitude measurements required accurate timekeeping, it wasn’t until the mid-18th century that longitude was easily and precisely measured at sea. Before then, sailors would often sail north or south to get to the desired latitude, then just head east or west until they reached the target longitude. Solving the longitude problem was so important that the British government passed the Longitude Act in 1714, offering a £20,000 prize to anyone who could devise a method of measuring longitude at sea to within half a degree. Many unsuccessful solutions were proposed, including astronomical observations, but it was a clock maker, John Harrison, who developed a series of clocks that eventually satisfied the criteria. The first version (the H1) weighed over 80 lbs, but his final timepieces, the H4 and H5, could be held in the palm of one hand. Ironically, even though his clocks satisfied the criteria, Harrison was never named as the winner of the longitude prize, and in fact no winner was ever officially determined. With accurate timepieces now available, a ship could have one clock set for Greenwich time (or some other home location), and another clock set to local time, which could be reset each day by observing the sun. The time difference between the two clocks could be used to calculate longitude.

Today we use GPS (Global Positioning System) technology to determine latitude and longitude, and even the smallest smart phones and smart watches can use GPS to calculate position. GPS works through a system of orbiting satellites that constantly emit signals containing the time and their position. A GPS receiver receives these signals from multiple satellites, and triangulates the signals to calculate position. The system needs 24 satellites to be functional at one time; as of 2015, the system consisted of about 32 operational satellites, able to give a position with an accuracy of 9 meters (30 feet) or less.

---

Additional links for more information:

• For more about John Harrison and the longitude problem, see http://www.rmg.co.uk/explore/astronomy-and-time/time-facts/harrison
• For more about the workings of GPS technology, visit https://www.gps.gov/