13.5: Lab Exercise (Part A)
- Page ID
- 5697
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Part A – Locating an Epicenter
You will determine the location of an earthquake epicenter using seismograms from Carrier, Oklahoma, Smith Ranch in Marlow, Oklahoma, and Bolivar Missouri available at the end of this chapter. These are actual seismograms that you will be reading, from an actual event. For each, three different readouts are given, as the seismograph measured in three different axes. You may focus on any of the three readouts for each station, as all will have the same arrival times for each wave. First, determine when the P and S waves arrived, and note these times (remember to look for a pattern change as lines get taller and more closely spaced). Mark both the arrival of the P-wave and S-wave, then using the time scale in seconds, note the time difference between the P and S wave arrivals. Add this to the table below for each of the three seismograms.
| Table 13.1 | ||||
| Station | P-wave Arrival Time (sec) | S-wave Arrival Time (sec) | Difference Between P and S Travel Times (sec) | Distance to Epicenter from Station (km) |
| Carrier, OK | ||||
| Marlow, OK | ||||
| Bolivar, MO | ||||
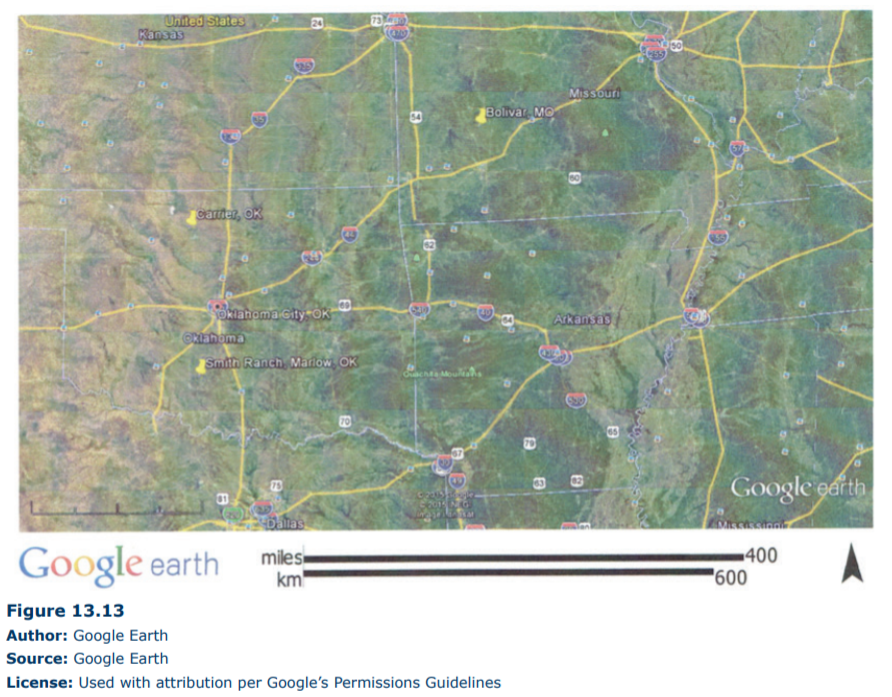
The difference between the P and S wave arrivals will be used to determine the distances to the epicenter from each station using Figure 13.11. Make sure that you use the curve for S-P Difference – find the seconds on the y-axis, read over to the S-P curve, then draw a line down to the x-axis for distance. Add the values to the table above. Now you need to create the circles from each station using Figure 13.13, a map with the three stations on it. This map includes a legend in kilometers. For each station, note the distance to the epicenter. Using a drafting compass (or alternately, tie a string to a pencil, cut the string the length of the distance to the epicenter, pin it at the station, and draw a circle, with the pencil stretched out the full distance of the string), you will create the circle. First, measure the scale on the map in Figure 13.13 in centimeters, and use that to convert your distances in kilometers to centimeters (ex. the map’s scale of 100 km = 2.1 cm on your ruler, so if you had a measured distance from one station of 400 km, that would equal 8.4 cm on your ruler). For this fictional example, starting at the station, use the drafting compass to make a circle that is 8.4 cm in radius. Create a circle for each of the three stations, using their different distances to the epicenter. They should overlap (or nearly overlap) in one location. The location where they overlap is the approximate epicenter of the earthquake. Once done, answer the questions below.
1. For Carrier, Oklahoma, what is the approximate time of the arrival of the first P-wave?
a. 10 seconds
b. 15 seconds
c. 21 seconds
d. 30 seconds
2. For Marlow, Oklahoma, what is the approximate time of the arrival of the first S-wave?
a. 19 seconds
b. 22 seconds
c. 35 seconds
d. 42 seconds
3. For Bolivar, Missouri, what is the difference between the P and S wave arrival times?
a. 10 seconds
b. 20 seconds
c. 40 seconds
d. 55 seconds
4. What is the approximate distance to the epicenter from Carrier, Oklahoma?
a. 70 km
b. 130 km
c. 240 km
d. 390 km
5. What is the approximate distance to the epicenter from Marlow, Oklahoma?
a. 70 km
b. 130 km
c. 240 km
d. 390 km
6. What is the approximate distance to the epicenter from Bolivar, Missouri?
a. 70 km
b. 130 km
c. 240 km
d. 390 km
7. Look at the location that you determined was the earthquake epicenter. Compare its location to Oklahoma City. Which direction is the epicenter located from Oklahoma City?
a. southeast
b. northwest
c. northeast
d. southwest
On January 12, 2010, a devastating magnitude 7.0 earthquake hit 16 miles west of Port-au-Prince, the capital of Haiti. At the following website, images are given of areas in Port-au-Prince both before the earthquake and soon after the earthquake, with a slider bar so that you can compare them.
Access these images at http://www.nytimes.com/interactive/2...i-imagery.html (or alternately at http://elearningexamples.com/the-des...t-au-prince-2/) and note the changes in many areas due to damage from the earthquake.
8. Examine the before and after image of the National Cathedral. Based on the changes seen within the structure, decide where this earthquake would most likely fall on the Modified Mercalli Intensity Scale. Based on this image, the most likely intensity of this earthquake would be:
a.<IV
b. V-VI
c. VII
d. VIII or greater
9. Residents in Port-au-Prince complained of extreme shaking during the earthquake, while residents of Santo Domingo, the capital of the Dominican Republic that sits 150 miles east of Port-au-Prince, assumed the shaking was caused by the passing of a large truck. Based on the Modified Mercalli Intensity Scale, the residents of Port-au-Prince mostly like experienced an intensity of _____, while the residents of Santo Domingo experienced an intensity of _____.
a. VII, II
b. VIII, III
c. X, III
d. X, IV


