12.9: Lab Exercise
- Page ID
- 5681
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Student Responses
This Lab Assignment must be mailed to your Instructor. There is no online assessment for the Crustal Deformation Lab.
Complete the entire assignment and mail to your instructor postmarked by the assessment deadline. You should make an extra copy to practice on and mail in a clean and neat version for grading. Make sure to include your name and staple all of the pages together. It is a good idea to make a copy of what you mail in, just in case it gets lost in the mail. For several parts of this lab, there are multiple interpretations! Ask if you have questions.
Part A (6 pts)
Circle the correct answer to the following questions.
1. For the following diagram, determine the correct map symbol that would go in the oval box.
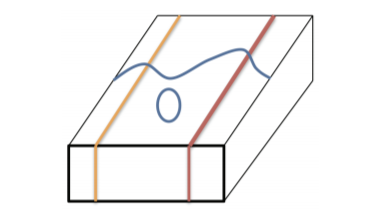
a. 
b. 
c.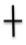
d.
2. For the following diagram, determine the correct map symbol that would go in the oval box.

a. 
b. 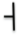
c.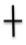
d.
3. Using Google Earth, search for the following area in Pakistan: 27 50 35.00N 67 10 03.70E. Zoom out to an eye altitude of approximately 25,000 feet. The inclined layers in these folded rocks can be easily seen. As you view them, in which compass direction are the beds dipping?
a. Northeast (NE)
b. Southeast (SE)
c. Northwest (NW)
d. Southwest (SW)
Part B (24 pts)
For each of the following block diagrams complete the following: 1- Complete the diagram drawing in geological contacts on each side of the block; 2- Add symbols indicating the strike and dip of each geological layer as well as symbols documenting any other geological features (include the direction of movement for any faults); 3- In the space provided under the block diagram write the specific name of the geology feature in the block diagram. Please note that in several of the blocks the ages of the layers are provided.
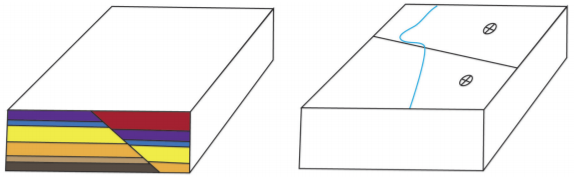
___________________________________ ___________________________________
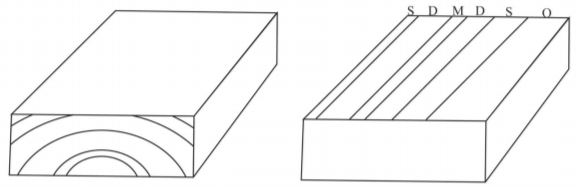
___________________________________ ___________________________________

___________________________________ ___________________________________
Part C (20 pts)
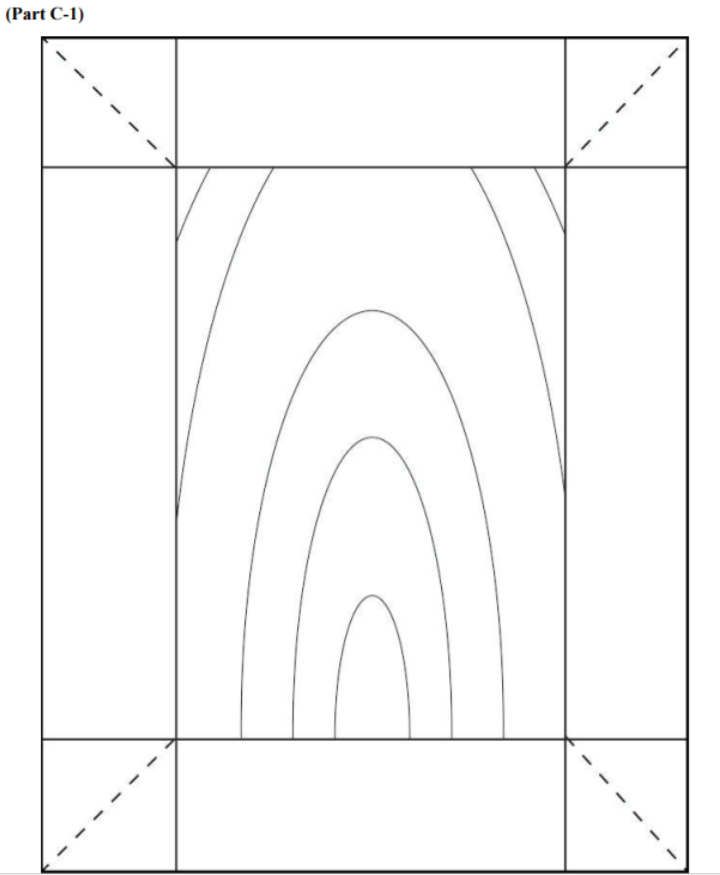
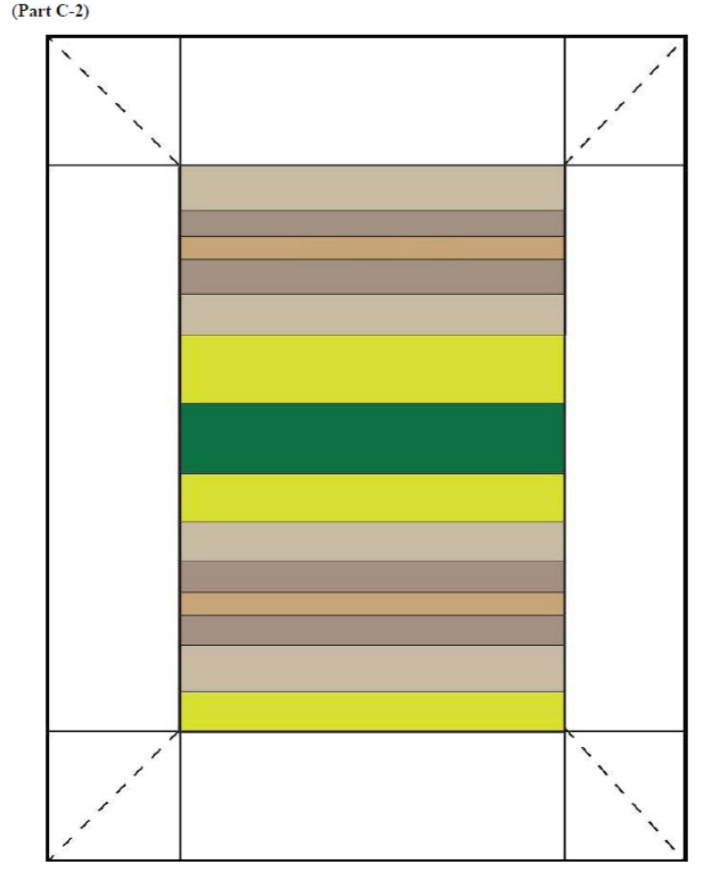
At the end of the lab, there are two full-page block diagrams. Cut along the dashed lines and fold along the solid lines to examine the block in three dimensions. For each of the block diagrams complete the following: 1- Complete the diagram drawing in geological contacts on each side of the block; 2- Add symbols indicating the strike and dip of each geological layer as well as symbols documenting any other geological features; 3- Identify the geologic structure presented on the block and write the name of the structure on the top surface of the block. Please unfold the blocks flat to mail in to your instructor.
Part D (24 pts)
The geological map on the following page is from the Paleozoic rocks in the Northwest Georgia Mountains. Please refer to the key to rocks and their ages present on the map in order to answer the questions. Note that the rock key is in chronological order with the oldest rocks on the bottom (Conasauga shale) and the youngest rocks on top (Pennsylvanian Fm).

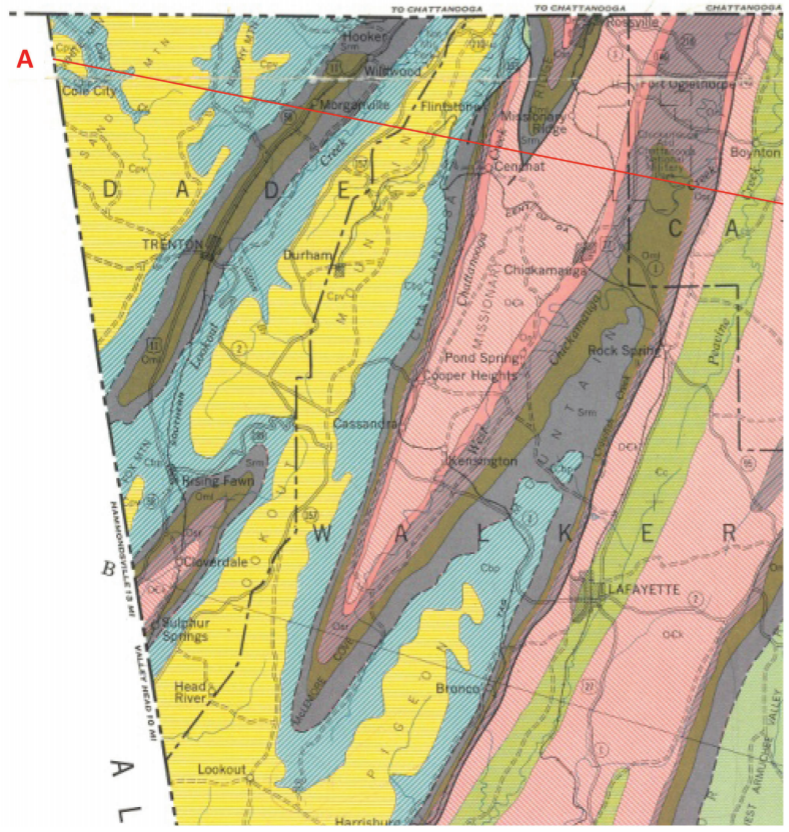
4. (6 pts) Examine the map and the ages of the rock layers. Based on your interpretation, label the structures and add appropriate symbols to the map to show the axis of the folds. What kinds of folds are present in this area? Explain how you came to this conclusion.
5. (6 pts) Along the red line starting at point ‘A’ there are four faults indicated by bold black lines (they are also marked on the cross section in Part C). Examine the age of the rocks and the faults themselves. What type of faults are these? Explain how you came to this conclusion.
6. (12 pts) Complete the following geological cross-section based on your understanding of the geological structures present in the area.

Part E - Google Earth (26 pts)
7. Search for 38 04 36.00N 109 55 26.61 W and zoom to an eye altitude of 20,000 ft, make sure to note your geographic location. (hint: re-read the section in the course content unit on Faults and in this lab manual)
a. You are looking at the surface expression of many fault lines (fault scarp) with the hanging wall occupying the valleys and the footwall representing the plateaus, what kind of faults are they?
b. What would we call these paired features?
e. How many of these faults would you need to make this area (Utah) a mile longer? Remember there are 5,280 feet in a mile.
c. What type of stress created these features?
d. The amount of displacement (extension or shortening) in the area can be calculated by the following equation based on the angle of the fault surface:
\[Amount \;of \;horizontal\; displacement = \frac{Vertical\; displacement \;along \;the\; fault\; surface\; (ft)}{5.67}\]
Measure the change in elevation of one of these features to determine the amount of extension in the area (Show your work, but feel free to use a calculator).
e. How many of these faults would you need to make this area (Utah) a mile longer? Remember there are 5,280 feet in a mile.
8. Search for 22 48 45.63S 117 20 12.85E and zoom to an eye altitude of 25 miles. This feature is caused by the folding of rocks.
a. Imagine you are a geologist trying to determine what is going on in the area. How could you tell if this large bullseye structure is a dome or a basin (State whether this is a dome or basin, and give two different ways to tell them apart)?
b. Examine the feature ~10 miles southwest of the previous feature. Is this fold horizontal or plunging, how can you tell?