5.3: Stream Gradient and the Cycle of Stream Erosion
- Page ID
- 5505
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Overview
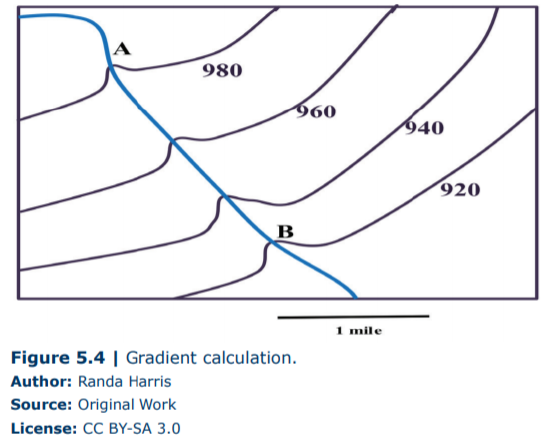
Stream gradient refers to the slope of the stream’s channel, or rise over run. It is the vertical drop of the stream over a horizontal distance. You have dealt with gradient before in Topographic Maps. It can be calculated using the following equation:
\[Gradient =\frac{(change \;in\; elevation)}{distance}\]
Let’s calculate the gradient from A to B in Figure 5.4 below. The elevation of the stream at A is 980’, and the elevation of the stream at B is 920’. Use the scale bar to calculate the distance from A to B. \[Gradient = \frac{(980’ – 920’)}{2 \;miles}, or\; \frac{30 \;feet}{mile}\].
Stream gradients tend to be higher in a stream’s headwaters (where it originates) and lower at their mouth, where they discharge into another body of water (such as the ocean). Discharge measures streamflow at a given time and location and specifically is a measure of the volume of water passing a particular point in a given period of time. It is found by multiplying the area (width multiplied by depth) of the stream channel by the velocity of the water and is often in units of cubic feet (or meters) per second. Discharge increases downstream in most rivers, as tributaries join the main channel and add water.
Sediment load (the amount of sediment carried by the stream) also changes from headwaters to mouth. At the headwaters, tributaries quickly carry their load downstream, combining with loads from other tributaries. The main river then eventually deposits that sediment load when it reaches base level. Sometimes in this process of carrying material downstream, the sediment load is large enough that the water is not capable of supporting it, so deposition occurs. If a stream becomes overloaded with sediment, braided streams may develop, with a network of intersecting channels that resembles braided hair. Sand and gravel bars are typical in braided streams, which are common in arid and semiarid regions with high erosion rates. Less commonly seen are straight streams, in which channels remain nearly straight, naturally due to a linear zone of weakness in the underlying rock. Straight channels can also be man-made, in an effort at flood control.
Streams may also be meandering, with broadly looping meanders that resemble “S”-shaped curves. The fastest water traveling in a meandering stream travels from outside bend to outside bend. This greater velocity and turbulence lead to more erosion on the outside bend, forming a featured called a cut bank. Erosion on this bank is offset by deposition on the opposite bank of the stream, where slower moving water allows sediment to settle out. These deposits are called point bars.
As meanders become more complicated, or sinuous, they may cut off a meander, discarding the meander to become a crescent-shaped oxbow lake. Check out Figure 5.6 to see the formation of an oxbow lake.

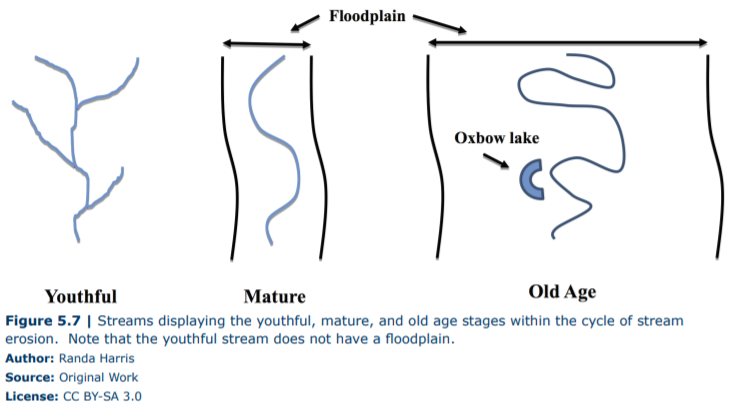
Even though streams are not living, they do go through characteristic changes over time as they change the landscape. The ultimate goal of a stream is to reach the base level (the low elevation at which the stream can no longer erode its channel often a lake or other stream; ultimate base level is the ocean). While trying to reach this goal, the stream will experience the cycle of stream erosion, which consists of these stages:
- Youthful (early) stage – these streams are downcutting their channels (vertically eroding); literally they are picking up sediment from the bottom of their channels in an effort to decrease their elevation. The land surface will be above sea level, and these streams form deep V-shaped channels.
- Mature (middle) stage – these streams experience both vertical (downcutting) and lateral (meandering) erosion. The land surface is sloped, and streams begin to form floodplains (the flat land around streams that are subject to flooding).
- Old age (late) stage – these streams focus on lateral erosion and have very complicated meanders and oxbow lakes. The land surface is near base level.
An interruption may occur in this cycle. If a stream suddenly begins to downcut again, if sea level dropped (so base level dropped) or if the area around it was uplifted (think building mountains), then the stream would become rejuvenated. If the rejuvenated stream was in the old age stage, it will begin to form a deep V-shaped channel within that complicated meandering pattern that it has. This creates a neat geologic feature called an entrenched meander (Figure 5.8).



