6.5: Earthquake Scaling Laws
- Page ID
- 3550
Big earthquakes, those 7 and above, are not very common. Smaller magnitude earthquakes occur much more frequently. There is a quantitative way of looking at the distributions of the occurrence of different magnitude earthquakes, the Gutenberg-Richter frequency-magnitude scaling law. Frequency-magnitude describes the number of occurrences as a function of magnitude.
\[log_{10}(N_c)=-bM+a\]
where M=magnitude, Nc=cumulative number of earthquakes that occurred with M \(\geq\) 0 (i.e. all earthquakes), a=total seismicity, and b='b value' which is the scaling value relating the number of large events to small events. a and b are constants calculated for a specific region and time.
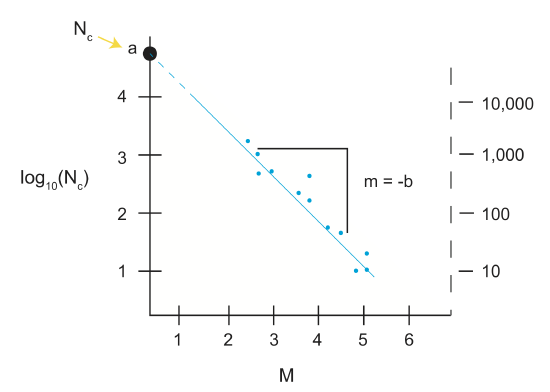
The scaling law is plotted on the above graph. The equation is a line (y=mx+b), where a gives the y-intercept and -b provides a negative slope.
Take a look at the three figures below:

We can see that linearity and fit of the Gutenberg-Richter law occurs in the mid-magnitude range. There are two reasons for this. One is roll-off. This is when small events are either not recorded or not detected among larger events (typically ~M 2). The other reason is a higher magnitude drop off. It is not physically possible to sustain this consistently for large magnitude events (typically ~M 4-5). In the Parkfield figure, there is a lower roll off. This is due to the dense network of seismometers around the area, which were installed as part of an experiment.
The most talked about part of the scaling relationship is the b value. The b value is typically \(0.8\leq b\leq 1.2\) with b \(\simeq\) 1. Since the relationship is logarithmic, when b=1, m=-1. Each M you go up by, you go down an order of magnitude of occurrence.
10,000 M2 events
1,000 M3
100 M4
10 M5
1 M6
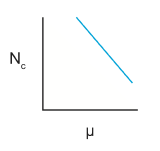
b \(\neq\)1 always. As b>1, you expect more smaller events relative to larger events (than for b=1).
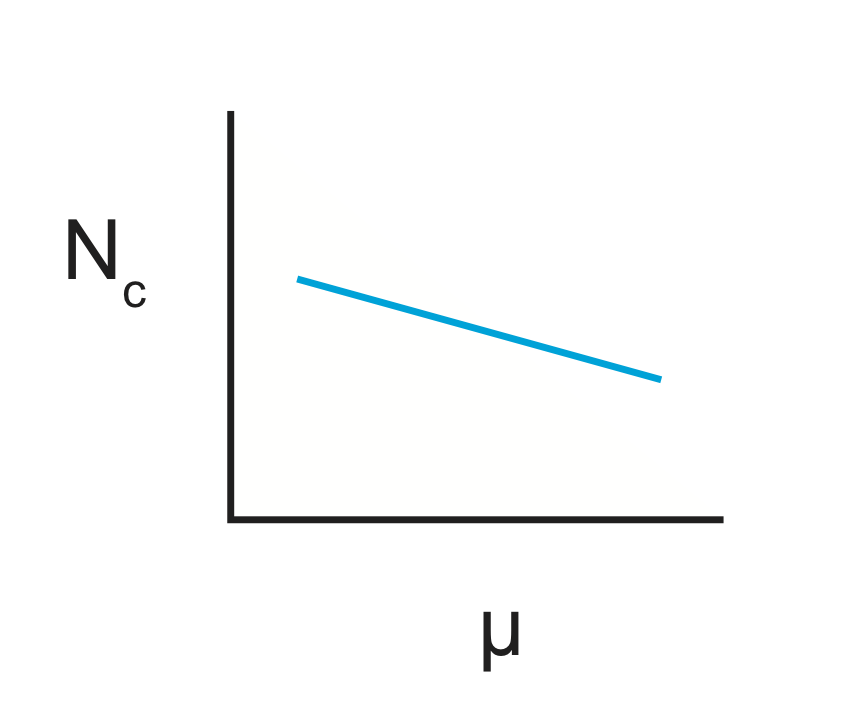
As b<1, you expect more larger events relative to smaller events (than for b=1).
.png?revision=1&size=bestfit&width=164&height=139)
a values are harder to compare than b values because they involve the total level of seismicity for a specific region and time.


