2.0: Introduction to Diffusion and Darcy's Law
- Page ID
- 4700
Diffusion is a concept many students are first introduced to in physics or chemistry. However, once the partial differential equation aspect of solving the diffusion equation is introduced, diffusion can seem like an intimidating and abstract concept. Simply put, diffusion is one process by which a substance moves from a region of high concentration to a region of low concentration. This is likely already a concept you are familiar with from everyday life, such as when you spray air freshener in one area of a room and then can smell it throughout the entire room, or how helium balloons from a party drop after several days as the helium diffuses out of the balloon.
In this chapter, we will cover the numerous practical uses and applications of the diffusion equation, and break down how exactly to solve the equations, so that they are far more approachable. The concept of diffusion can also be used as a physical model to simulate more complicated process, such as erosion of a fault scarp. Understanding diffusion will give you greater insight into how geologic processes function, such as cooling of a magma dike, the cooling of the lithosphere, diffusion of atoms in/out of grains (e.g., the primary process of rock metamorphism) and erosion of fault scarps. The chapter will also cover Darcy's law, which is based on diffusion and is used to model how a fluid moves through a porous medium.
By the end of this chapter, you should be comfortable with heat flow in one dimension, the origin of the diffusion equation and Darcy's Law, and how to apply these concepts to other processes, such as chemical diffusion and erosion. Additionally, you will gains skills in considering the boundary conditions that are needed to solve the partial differential equation that describes diffusion, specifically for various geologic processes.
Examples of Diffusive Processes in the Geosciences
There are many applications and uses of the diffusion equation in geosciences, from diffusion of an element within a solid at the lattice-scale, to diffusion of heat at a local to regional scale, to diffusion of topography, and diffusion of a chemical species in the crust. Before we dive head first into the diffusion equation, let's look at four examples of how it can be applied. For all of these examples there is a diffusion coefficient (diffusivity) that controls how the parameter of interest (e.g., temperature, concentration) will move through the surroundings.
Heat conduction (\(T(\overrightarrow{x},t\)))
A localized temperature perturbation will slowly cool off as it heats up the surrounding region. The temperature profile (\(T(x)\)) at any time, t, depends on the initial temperature distribution and how quickly heat diffuses into the surrounding material. For this example the thermal diffusivity controls the rate of heat conduction.
- a. Dike emplacement in the crust: How long does it take for the heat to diffuse into the surrounding region?
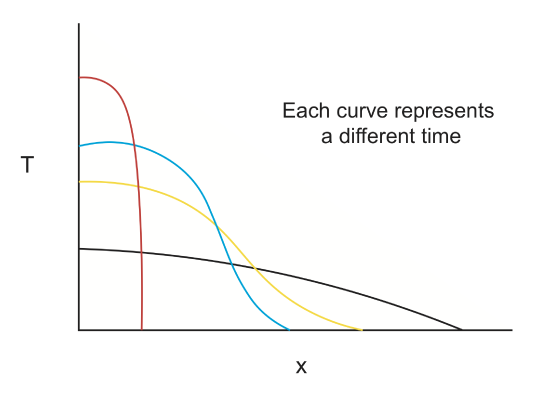
- b. Cooling/aging of the crust/lithosphere: As the crust and lithosphere cool by thermal conduction the tectonic plate becomes denser and subside. This is the reason that old lithosphere becomes progressively deeper as it moves away from a mid-ocean spreading center. Conduction of heat out the the lithophere is a diffusive process.
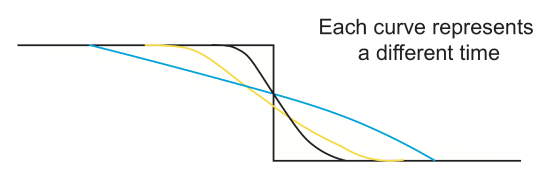
Erosion of a fault scarp (\(H(\overrightarrow{x},t\)))
The sharp topography formed at the surface when a fault ruptures with vertical component of displacement will slowly erode away with time. At first, the cross section will look like a step function. After some amount of time, the sharp corners will fill in or erode away, until slowly the sharp offset becomes a smoothly dipping slope. The shape of this eroding offset with time can be modeled as a diffusive process even though the true physical process is more complex.
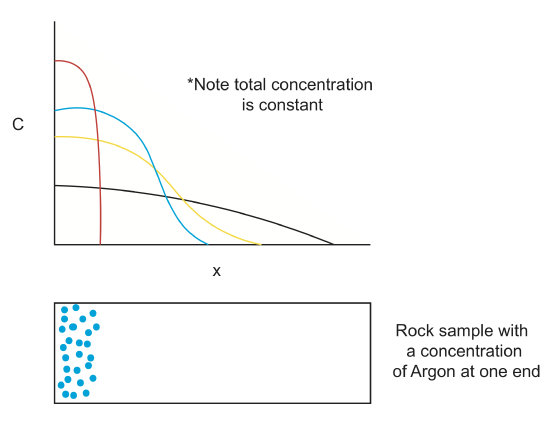
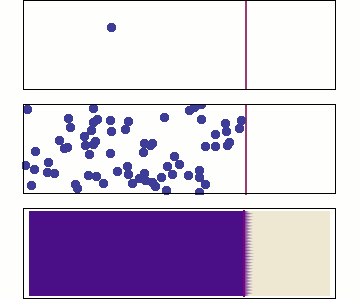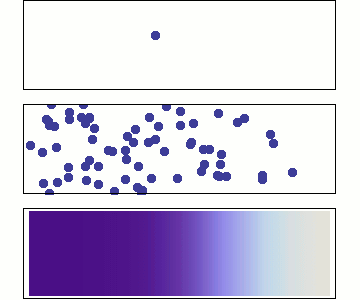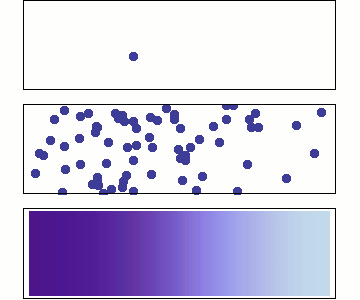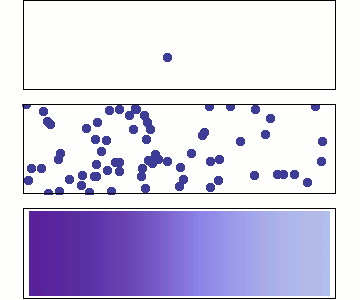
Chemical diffusion (\(C(\overrightarrow{x},t\)))
Chemical diffusion of elements within a rock lattice structure is also described by a diffusion equation for the concentration of a chemical species. Chemical diffusion is important for understanding radiogenic dating of rocks (when does loss by diffusion stop?), solid-state diffusion (which is the primary process by which rocks metamorphose), diffusion of toxic chemicals from dump sites and diffusion of "chemical plumes" associated with nuclear waste leaks.