2.1: The Diffusion Equation
- Page ID
- 3526
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We will start the discussion of diffusion by considering the familiar process of thermal conduction.
Thermal Conduction
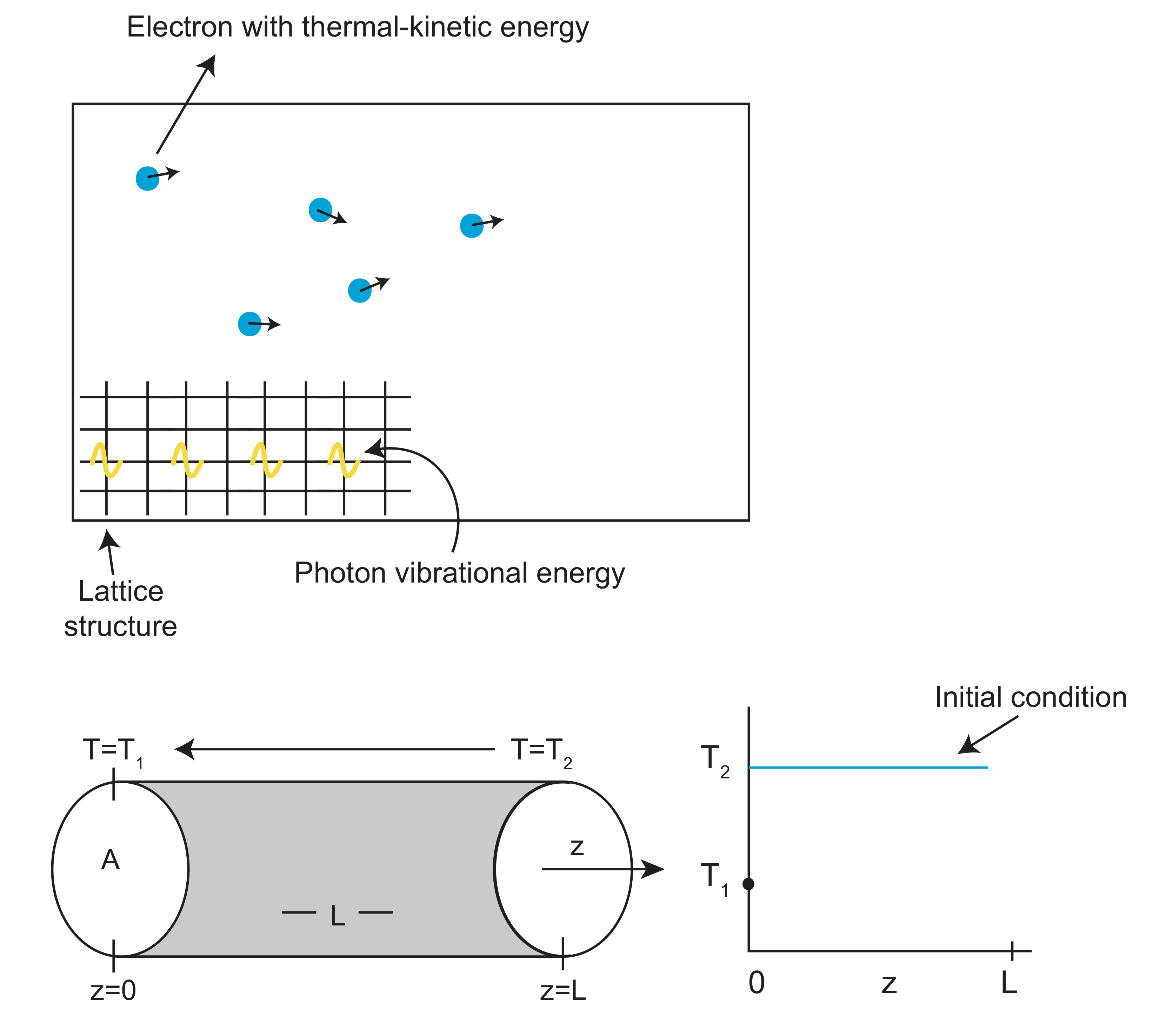
Diffusion of heat through a crystal lattice occurs through two processes. First, heat can be carried by electrons in the form of kinetic energy in metallic rocks. If a region of the rock is heated at one end, the thermal energy excites the electrons, giving them extra energy to move through the rock from regions of high heat to regions of low heat. As the electrons moves, they lose some of this extra energy as heat, thus heating up the region they have moved to. Second, heating a lattice structure adds kinetic energy to the lattice itself, by increasing the vibrational bonds between atoms (think of atoms connected to each other by little springs). The movement of this vibrational energy through the lattice structure is termed a phonon. Both modes of passing energy through the lattice structure act to conduct heat from regions of higher temperature to regions of lower temperature, changing the distribution (and perhaps the total amount) of heat within the rock.
Heat Flow Equation: A 1-D Rod
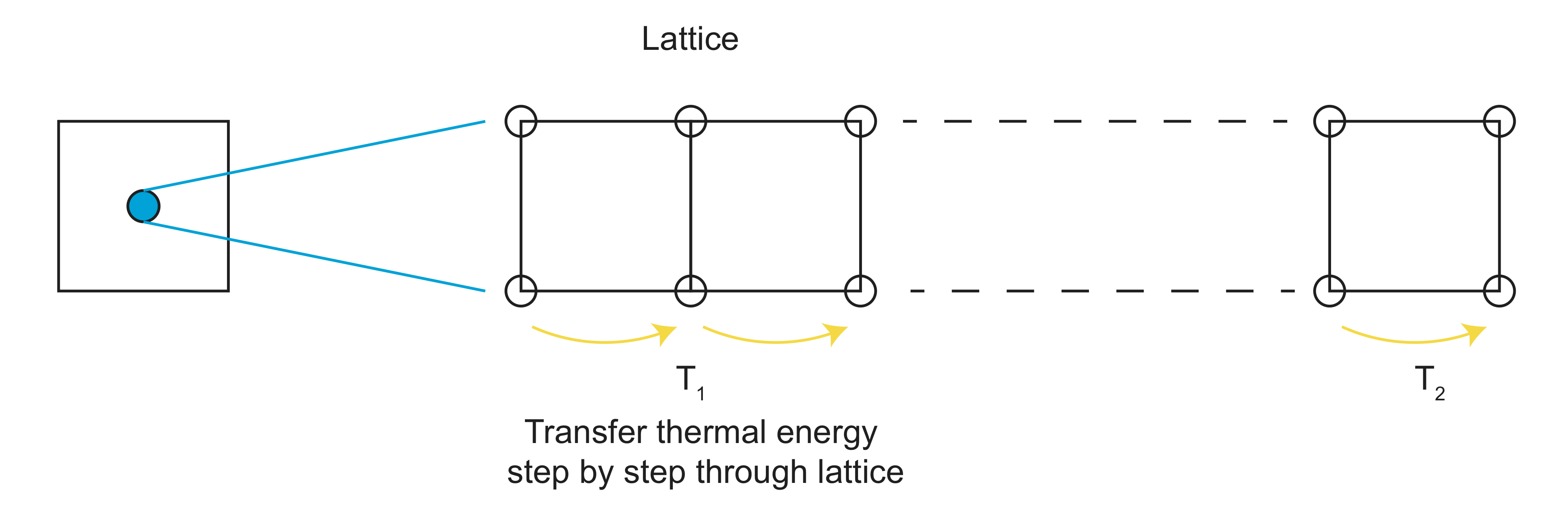
Start with a cylindrical rod, of length \(L\), and cross-sectional area \(A\), aligned with the z axis. Fix the temperature at \(z=0\) to \(T_1\) and the temperature from \(z>0\) to \(z=L\) to \(T_2\), where \(T_2>T_1\). The heat, \(Q\), will move from the high temperature region to the low temperature region, in the -z direction.
The change in heat within the rod, \(\Delta Q\), is given by:
\[\Delta Q=kA\left(d\frac{T_2-T_1}{L}\right)\Delta t \nonumber\]
where \(k\) is the thermal conductivity with units of \(\frac{W}{mK}\)(watts per meter Kelvin). Therefore, \(\Delta Q\) has units of joules (note 1 W=1\(\frac{J}{s}\)). Rearrange the equation above as,
\[\frac{\Delta Q}{A\Delta t}=k\frac{\Delta T}{L} \nonumber\]
The left hand side is the change in heat per unit area per unit time, which is a heat flux, given the symbol, \(q\).
\[q=\frac{1}{A} \frac{dQ}{dt} \nonumber\]
Substituting \(q\) into the equation above and then rewriting the other side as a full derivative we arrive at the Heat Flow Equation:
\[q=-k\frac{dT}{dz} \label{heat}\]
Note, that the minus sign shows that the heat moves in the -z direction from high temperature to low temperature.
Diffusion Equation for a 3-D Volume
More generally, we should consider a 3-D volume element (of a rock) and examine how the heat content changes within this volume as a function of time. Consider a cubic volume element with sides of length \(dx\), \(dy\), and \(dz\) and volume, \(dV=dxdydz\).

Consider heat flowing along the z axis. The heat that enters the volume at z+dz is \(Q_z\) and the heat that leaves the volume at z is \(Q_z -dQ_z\). The change in heat within the volume is then:
\[\Delta Q=Q_z-(Q_z-dQz) \nonumber\]
We an rerewrite as:
\[\Delta Q=Q_z-(Q_z-\left(\dfrac{dQz}{dz}\right)(-dz)) \nonumber\]
then,
\[\Delta Q=-\left(\frac{dQz}{dz}\right)dz \nonumber\]
From the heat flow equation (Equation \ref{heat}) we also know that
\[q=\frac{1}{A} \frac{dQ}{dt} \nonumber\]
or
\[dQ=qA\,dt \nonumber\]
where
\[q=-k\frac{dT}{dz}. \nonumber\]
Substituting \(q\) into the equation for \(dQ\) and then subsituting \(dQ\) into the equation for \(\Delta q\) we find,
\[\Delta Q=-\frac{d}{dz}(qAdt)dz=-\frac{d}{dz}(-k\frac{dT}{dz})dV\,dt \nonumber\]
where \(dV=Adz=dxdydz\). If the conductivity, \(k\), is independent of position (a constant throughout the rock), then this can be written as:
\[\Delta Q=k(\frac{d^2T}{dz^2})dV\, dt \nonumber\]
where both negative signs have canceled out so that \(\Delta Q\) is positive. This equation states that the changes the heat flux in the volume element of the rock are proportional to the curvature (second derivative) of the temperature profile. This is interesting, because we usually think of conduction as being faster where the gradient is largest, but its actually faster where the change in gradient is the largest.
The total heat within the rock can also be considered from the perspective of the total heat capacity of the rock (how much heat can the rock hold), which depends on the specific heat, \(c\), and the density, \(\rho\), of the rock:
\[\Delta Q=c\rho dV\Delta T \nonumber\]
Setting the two expressions for \(\Delta Q\) equal:
\[c\rho dV\Delta T= k(\frac{d^2T}{dz^2})dV dt \nonumber\]
which can be rearranged as,
\[\frac{dT}{dt}=\frac{k}{c\rho}\frac{d^2T}{dz^2} \nonumber\]
where \(dT\) has been substituted for \(\Delta T\). The combination of physical constants, \(\frac{k}{c\rho}\) is the thermal diffusivity and has units of \((\frac{m^2}{s})\). The thermal diffusivity is given the greek symbol \(\kappa\) (kappa). Substituting in \(\kappa\) we arrive at the 1-D Diffusion Equation:
\[\frac{dT}{dt}=\kappa\frac{d^2T}{dz^2} \nonumber\]
Note, this equation relates the change in temperature per unit time to the curvature of the temperature profile in the direction of heat flow.
Full Form of the Diffusion Equation
In general, heat flow can come from any direction, so the temperature will depend on x, y, z, and t. Because \(T=T(x, y, z, t)\) and is not just dependent on one variable, it is necessary to rewrite the derivatives in the diffusion equation as partial derivatives:
\[\frac{\partial T}{\partial t}=\kappa \left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}+\frac{\partial^2 T}{\partial z^2}\right) \nonumber \]
In this case for example, for the partial derivative with respect to time, each of the variables (x, y, z) are treated as constants, and so on for each other variable. Don’t let the partial derivatives confuse you, they are just derivatives. In general, you still want to think of this equation as a bunch of small changes in temperature, \(\Delta T\), occurring over small intervals of time, \(\Delta t\), and over small distances (\(\Delta z\)):
\[\frac{\Delta T}{\Delta t}=\kappa\frac{\Delta T}{(\Delta z)^2} \nonumber\]
This is the "Simplified Diffusion Equation"
Estimating Time/Length-scale for Diffusive Processes
Length-scale of Diffusion
The above simplified version of the diffusion equation can be solved for \(\Delta z\) to give an indication of how far heat can move in a given amount of time:
\[\Delta z\simeq\sqrt{\kappa\Delta t} \nonumber\]
For the earth, a good average value for the thermal diffusivity is \(\kappa=1x10^{-6}\frac{m^2}{s}\). How far does heat diffuse through a rock in 1 million years?
\[\Delta z=\sqrt{(1x10^{-6})(1x10^6)(3.15x10^7)} \nonumber\]
where there are about \(3.15 \times 10^7\) sec per year,
\[\Delta z\simeq 5.6\; km\]
What does this length-scale tell us? It does not tell us the temperature at any particular distance, but instead tells us that a noticeable amount of heat will have travel this distance in the time specified.
Time-scale of Diffusion
Another way of building your intuition for diffusion is to solve the simplified diffusion equation for \(\Delta t\):
\[\Delta t\simeq\frac{\Delta z^2}{\kappa} \nonumber\]
We can use this time-scale to consider the question How long does it take for heat magma intrusion to affect the surrounding rock 100 m away?
\[\Delta t=\frac{(100^2)}{(1x10^{-6})(3.15x10^7)} \nonumber\]
\[\Delta t=318\;years.\]
What does this timescale tell us? It does not tell us the temperature at the distance specified, but instead tells us that a noticeable amount of heat will have reached the distance specified in this time.
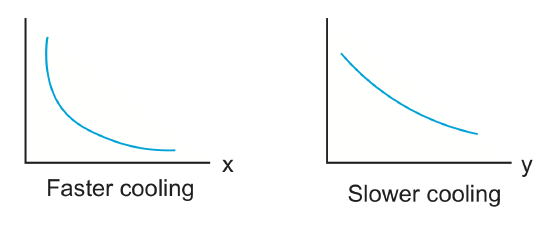
It is important to keep in mind that the temperature gradient, which controls the heat flux, changes both spatially and temporally, so heat transport is faster initially, and slower later on. So, the diffusion time-scale and length-scale really just give an order of magnitude estimate of the time-scales and length-scales that will be important in the problem.
Diffusivity and Diffusion in 1, 2, or 3 Dimensions
Note that \(\kappa\) has units of \(\frac{m^2}{s}\), which does not depend on temperature or heat flow. Diffusivity, in general, describes the spreading out of some quantity (e.g. temperature, concentration) through an area in some unit of time. Each diffusion processes will have it own diffusivity, which quantifies how the diffuses process occurs for that material. Each diffusivity will have same units, \(\frac{m^2}{s}\), no matter which diffusive process is being considered.
If \(\kappa\) is a constant (which it usually is) then diffusion will be isotropic (the same in all directions). However, remember that if there are initial differences in the temperature gradients (due to how the initial temperature disturbance occurred), then the rate of cooling or heating can be different in different directions.
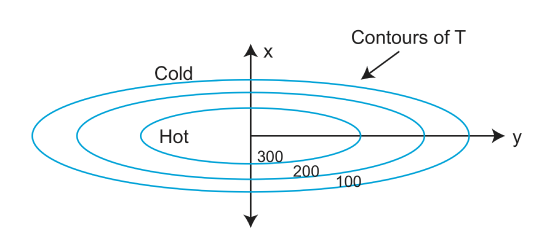
The contours on the above figure are analogous to the contours on a topographic map. The contours are spaced closely in the x direction and so the temperature gradient is large there. Thus, the higher the degree of curvature on the graph indicates the direction of maximum cooling or heating.