1.4: The Nature of Water

1.4.1 Introduction

Human beings in general, and often even scientists in particular, are inclined to take water for granted: it’s almost literally everywhere, and we can’t live without it. It’s difficult to cite a process—physical chemical, or biological— operating on or near the Earth’s surface that doesn’t involve water in a substantial if not essential way. Because water seems so ordinary, we tend to judge the behavior of so many other substances with reference to it. In reality, however, water is a highly unusual compound, greatly different in many (but by no means all) of its properties and aspects of behavior than what one would expect in view of its apparently simple composition and low molecular weight. Just one example should suffice here: the expansion when solid water thaws to liquid water. This is close to being unique, and it has profound implications for processes and life on the Earth's surface.

This section attempts a survey of the nature and properties of water. Its goal is to show you the most important facts about the nature and relationships among water in its solid, liquid, and gaseous states, and how these can be explained on the molecular level. The latter endeavor will necessarily be somewhat superficial, because a fundamental approach to the behavior of water is heavily quantum-mechanical, and also because there is still much that’s not well understood.

1.4.2 The Water Molecule

The unusual properties of water are a direct consequence of the structure of the H2O molecule, so I’ll give you some facts about its geometry, structure, and electrical state before looking at the behavior and properties of water.

It is well established that the water molecule consists of two atoms of hydrogen and one atom of oxygen arranged as an isosceles triangle. The H–O–H angle is about 104.5°, and the O–H bond length is very close to 0.1 nm (nanometers; 10-9 meters). Assuming the effective atomic radius of the oxygen to be 0.14 nm and that of the hydrogens to be 0.12 nm, one way of schematizing the water molecule is shown in Figure 1-24. It’s known that this basic geometry is little affected by the changing environment of the molecule in the gas, liquid, or solid form over a wide range of temperatures and pressures.

Figure 1-24. Cartoon of the water molecule, showing O–H distance, H–O–H angle, and effective radii of the hydrogen and the oxygen.

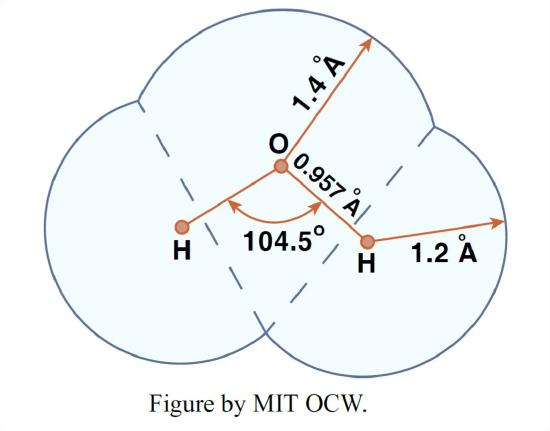
Keep in mind, however, that the picture in Figure 1-24 is something of a fake, because what really governs what the molecule looks like to the outside world is the electron distribution around the three nuclei, because that’s what determines how close you can get to the molecule from any given direction before enormous repulsive forces build up as you try to penetrate the electron field.

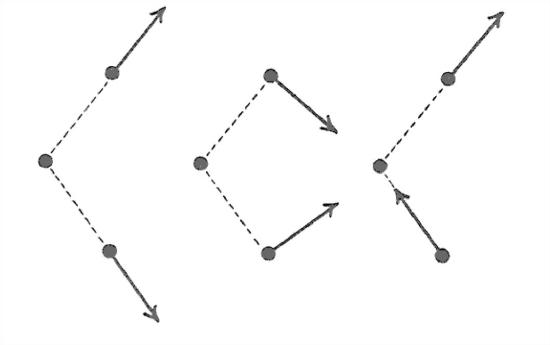
The three nuclei of the water molecule are always undergoing vibrations, of three kinds (Figure 1-25): the two hydrogens oscillate back and forth along the oxygen–hydrogen directions in phase (this is called the symmetric stretching vibration); the two hydrogens oscillate back and forth along the oxygen–hydrogen directions a half cycle out of phase (this is called the asymmetric stretching vibration); and the two hydrogens move in phase in opposite directions along circular arcs lying in the plane of the molecule (this is called the bending vibration). These are the fundamental or normal modes of the vibration; the actual vibration is a linear superposition of these (in other words, they all add up together, without any one affecting either of the others). The periods of the oscillations are extremely small—of the order of 10-14 s!

Figure 1-25. Modes of vibration of the water molecule.

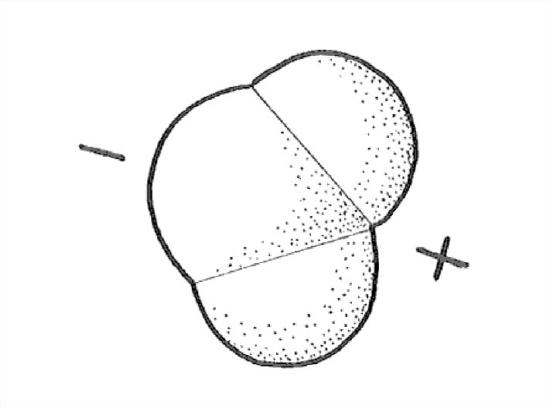
The distribution of the electrons, in space, in and around the water molecule—the most important feature of the molecule in terms of bonding—is not what you might guess. Because oxygen is near the right side of the periodic table and hydrogen is at the left side, it should seem reasonable that the electrons tend to be more in the vicinity of the oxygen than in the vicinity of the hydrogens. The molecule is thus what is called a polar molecule: the oxygen “end” or “side” has a negative electric charge, and the hydrogen “end” or “side” has a positive electric charge (Figure 1-26).

Figure 1-26. Overall distribution of electric charge on the water molecule.

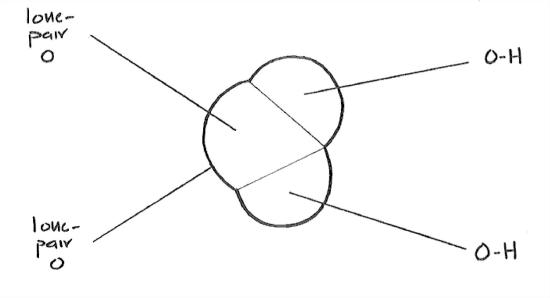
But a more fundamental way of viewing the electron distribution of the water molecule (a way that is beyond the scope of this course) has to do with the quantum-mechanical structure of the electron “orbits”, or, more properly, electron orbitals. The six electrons in the outermost electron shell of the oxygen (those are the ones involved in bonding with other atoms) turn out to be in equivalent orbitals, and the way you can arrange four directions in space in the most equivalent or non-preferential way is tetrahedrally—that is, starting from the center of a tetrahedron, in the directions toward the four vertices of the tetrahedron (Figure 1-27). Two of these tetrahedral positions are associated with the bonding with the two hydrogens, and the other two are what I’ll call very unofficially here the open positions. Figure 1-28 is a crude sketch of the geometry of the bonding directions.

Figure 1-27. A tetrahedron.

Figure 1-28. Geometry of bonding directions in the water molecule.

1.4.3 Ice

We’ll look at the structure of ice before worrying about liquid water, because its structure is well known, thanks to the technique of x-ray diffraction. The ice that you and I are familiar with is known as ice I (or, more precisely, ice Ih). This is the form of ice that’s found at room pressures and low temperatures. At higher pressures several other polymorphs of ice make their appearance, but they never occur under the conditions of the earth’s surface and atmosphere. (Minerals that have the same composition but different crystal structure are called polymorphs of one another.)

The most striking and very unusual thing about ice Ih is the openness of its structure. This arises from the way water molecules are bonded to one another. Water molecules are bonded by what are called hydrogen bonds (Figure 1-29): one of the hydrogen atoms of one molecule is bonded electrostatically to the oxygen atom of the other molecule, in such a way that the hydrogen is attached to the oxygen at one of the open positions—of which there are two, remember, in tetrahedral relationship to each other.

Figure 1-29. The hydrogen bond. (the atoms at the ends of the bond should be touching.)

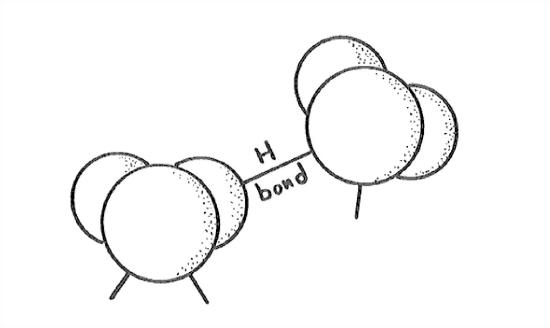
The hydrogen bond is not nearly as strong as the very strong oxygen– hydrogen bonds within the water molecule itself, but it’s strong enough to promote bonding to form a stable crystal structure (and, as you will see soon, liquid water too) at temperatures much higher than we have any right to expect.

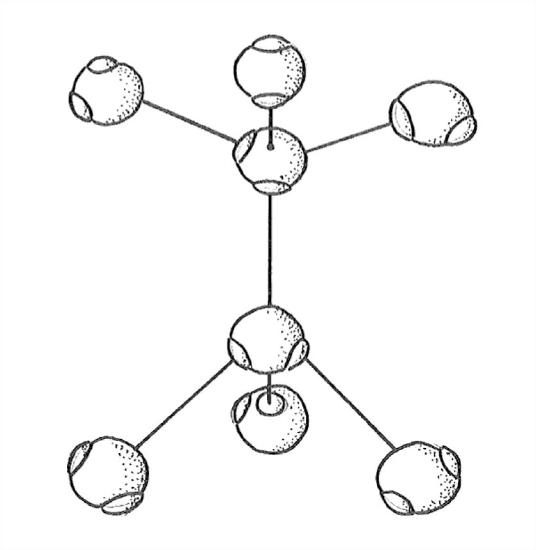
In the ice structure, each water molecule is surrounded by, and hydrogen-bonded to, four water molecules, arranged tetrahedrally around that given water molecule. Two of these nearest-neighbor water molecules have one of their hydrogens bonded at the open positions of the oxygen of the given water molecule, and each of the other two nearest-neighbor water molecules have one of the open positions of its oxygen bonded to one of the hydrogens of the given water molecule.

Does that sound too complicated? Read the last paragraph through again, and then look at Figure 1-30, which is a blown-up view of this tetrahedral hydrogen-bonding arrangement, the best I can draw it for you. When looking at Figure 1-30, keep in mind that all the water molecules should really be touching.

Figure 1-30. Blown-up view of the tetrahedral hydrogen-bonding arrangement in ice.

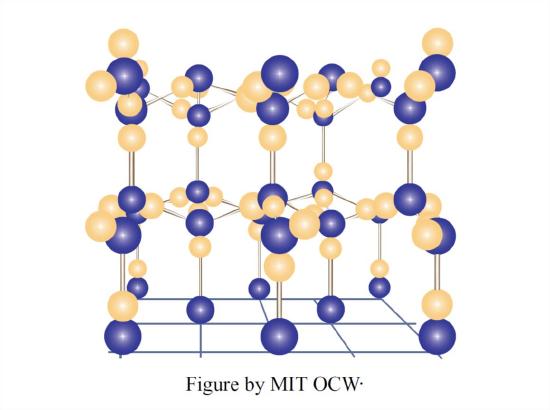
To build up the ice structure, I want you now to imagine starting with the top four of the five-molecule tetrahedral arrangement in Figure 1-30 and adding water molecules in all horizontal directions, to form a kind of puckered sheet (unofficial term). Then stack puckered sheet upon puckered sheet and bond them together by means of the vertically upward-directed and downward-directed fourth bonds extending from each molecule in each puckered sheet. Figure 1-31 is a sketch of just one little segment of two adjacent puckered sheets, viewed from the side.

Figure 1-31. Blown-up sketch of one small segment of two adjacent “puckered sheets” in the ice structure.

If you stretch your powers of three-dimensional visualization a little more, you’ll see that the puckered sheets have hexagonal symmetry when viewed normal to the sheets. Figure 1-32 shows schematically the arrangement of the water molecules in one of the puckered sheets. The water molecules in the sheet are alternately high and low, and are so labeled H and L in Figure 1-32.

Figure 1-32. Schematic arrangement of water molecules in a “puckered sheet” in the ice structure. The circled numbers correspond to those shown in Figure 1-31.

So the ice structure is one of hexagonal symmetry, with big columns of empty space down the middles of the hexagons. A view from the side (Figure 1- 33) suggests (but does not show too well in the figure) open tunnels running normal to the hexagonal axis also. The hexagonal symmetry axis is called the c axis, and the plane parallel to the puckered sheets is called the basal plane.

What is striking about this hexagonally symmetric ice structure is its openness. If the hydrogen bonding did not happen, and the water molecules were close packed, each would be surrounded by twelve nearest neighbors instead of four, and the structure of ice would be much denser than it actually is. This is the fundamental reason why the solid phase, ice, is less dense than the liquid phase. (That seemingly simple little statement has profound implications for water on the Earth.) Only a handful of other substances, germanium and silicon among them, show this behavior.

Figure 1-33. Side view of the ice structure.

1.4.4 Liquid Water

I said in an earlier section that the liquid state is complicated and relatively poorly understood. This is true even more so for water, because of the existence of those unusual hydrogen bonds. Here I will concentrate on some of the unusual properties of liquid water and make some qualitative comments on how they might be explained.

First off, think about the density of water as a function of temperature and pressure. The pressure dependence of the density is not out of the ordinary: water has a certain small compressibility, not out of line with other liquids. But the temperature behavior is astounding (Figure 1-34): at constant pressure the density of liquid water actually increases with increasing temperature from 0°C to about 4°C and then slowly decreases with increasing temperature above that magic 4°C temperature.

Keep in mind also that the density increases in the transition from ice to liquid water upon melting at room pressures, from about 0.92 g/cm3 to 1.00 g/cm3. When most solids melt to their liquid phase, the structure opens up a little, as the molecular ordering decreases and the molecules become partially free to wander relative to their nearest neighbors. But the opposite is true for water: the packing of the molecules in liquid water is actually greater than in ice.

The best way to explain the behavior of water density with temperature is to postulate that the melting of ice involves breakage of some of the hydrogen bonds, so that there is a partial collapse to closer packing. Models of the liquid water state tend to assume that there are transient and local ice-like structural regions with complete hydrogen bonding (called, expressively, “flickering clusters”), and other transient and local regions in which the water molecules are more closely packed. As the temperature of the liquid increases, a greater and greater percentage of the molecules are in a close-packed state, leading to the amazing increase in density from 0°C to 4°C.

Figure 1-34. Graph of density against temperature for ice and pure liquid water. (From Gross, 1990.)

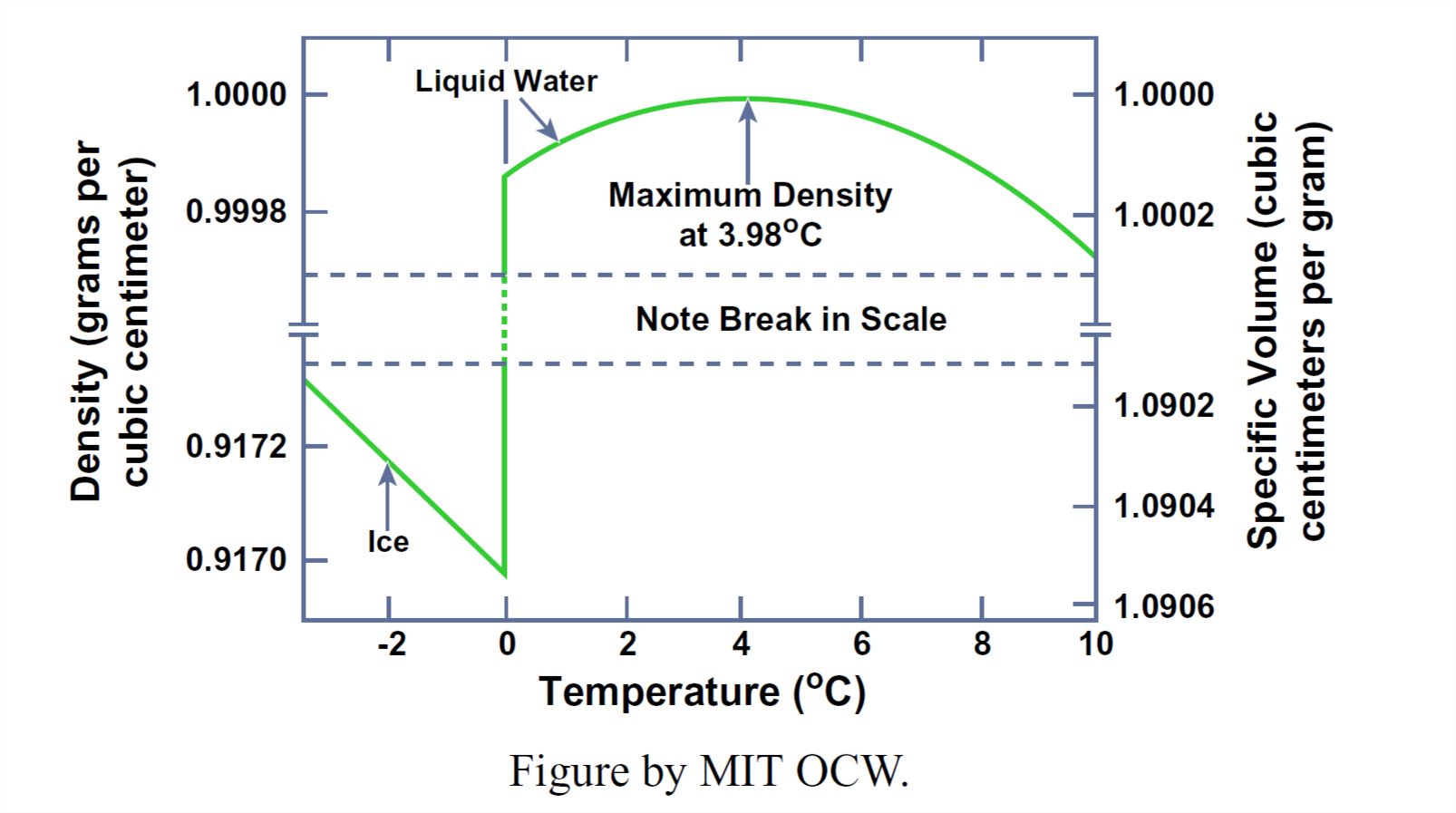
Counteracting the hydrogen-bond-breaking tendency is the normal tendency for overall increase in the separation distance of all the molecules in the aggregate due to increase in thermal agitation of the molecules as the temperature increases. At temperatures greater than 4°C, this expansion effect more than counteracts the condensation effect due to breaking of hydrogen bonds.

Another outstanding feature of liquid water is its extremely high heat of vaporization, about 540 cal/g. This is almost an order of magnitude higher than what might be expected for normal liquids of the same molecular weight. Why so high? Again one can invoke the progressively smaller percentage of hydrogen bonds per unit mass of water. It takes energy to break the hydrogen bonds, and that’s what shows up as additional heat of vaporization, in addition to the usual contribution that goes into detaching molecules of the liquid from the liquid–vapor interface, where they are held tightly by the attractive forces of the subjacent molecules.

The specific heat capacity of liquid water is extremely high, for the same reason: as heat is added to liquid water, not only does it go toward increasing the thermal energy of vibrations of the water molecules; it also has to go toward breaking more and more of the remaining hydrogen bonds, which takes energy.

Finally, it’s worth pointing out that many important properties of liquid water are not out of the ordinary. Properties that involve molecular transport, like the coefficient of viscosity and the coefficient of diffusion are in line with what would be expected of a normal liquid.

1.4.5 Phase Equilibrium in Water

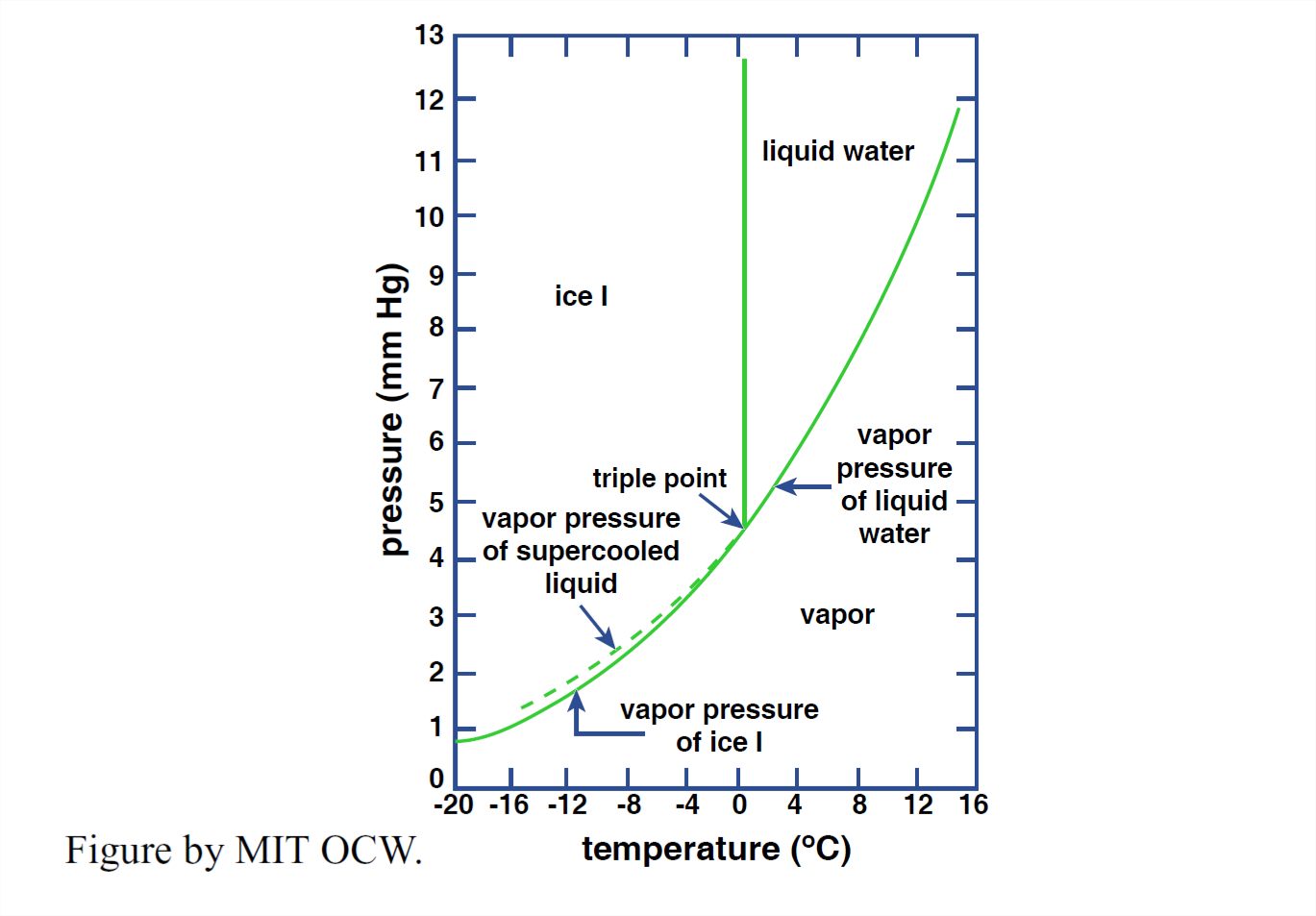
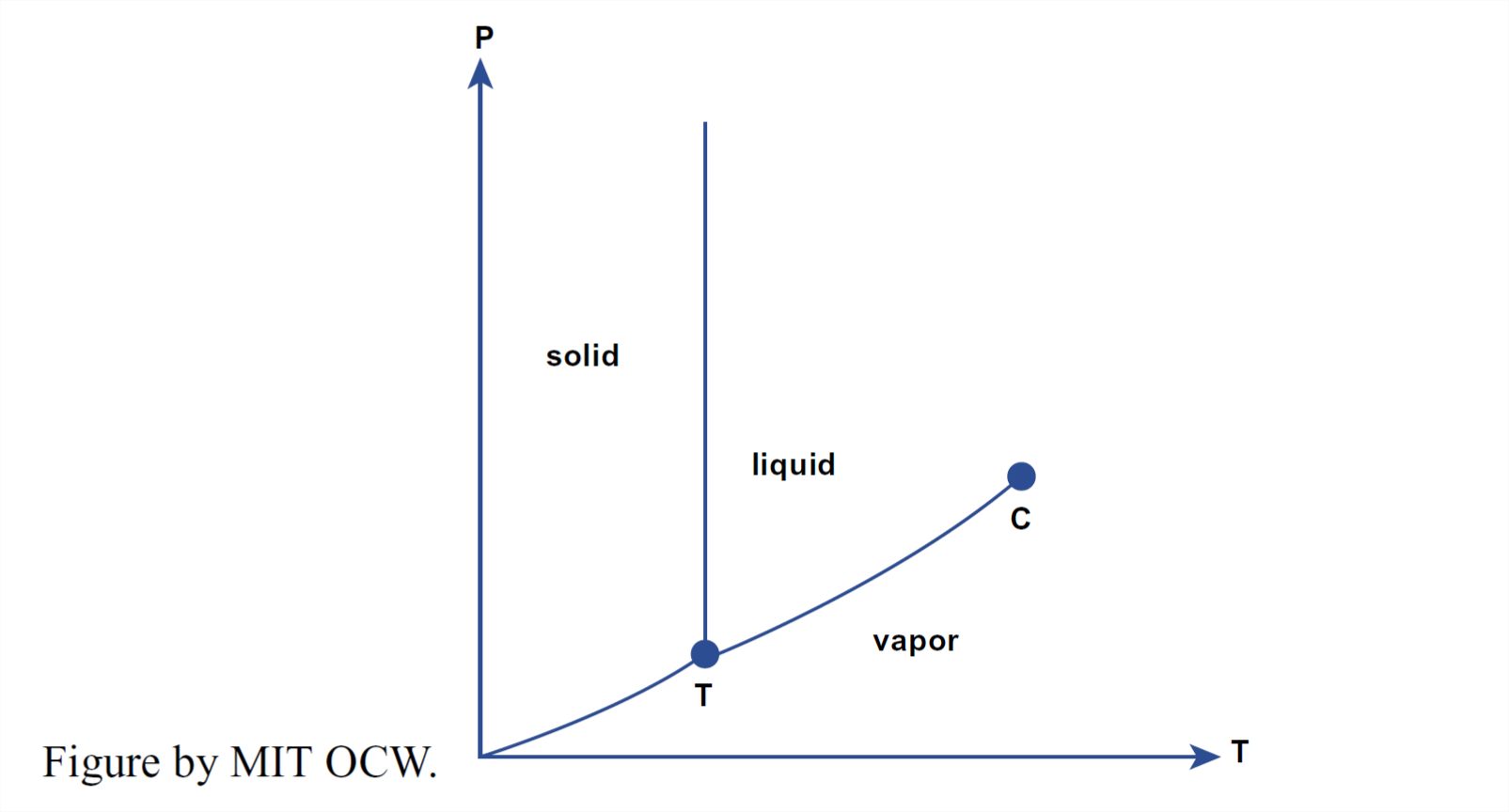
Now that we have surveyed the structure of solid and liquid water, it’s time to look at the equilibrium among the solid phase, the liquid phase, and the vapor phase. The best way to do this is by means of a phase diagram, which shows the ranges of pressure P and temperature T characteristic of each phase and the sets of pressures and temperatures for which two (or even all three) phases can coexist with one another at equilibrium. Figure 1-35 shows such a diagram for water—but only for very low pressures, much less than atmospheric. Figure 1-36 is a simplified “cartoon” version of Figure 1-35.

What are the important features of the phase diagram in Figures 1-35 and 1-36? Note first that way down near the lower left corner there is an unobtrusive triple point among the vapor, liquid, and solid phases. At that particular set of values of T and P (at a temperature of about 0.1°C and a pressure of about 4.6 mm Hg, or about 6 x 10-3 atmospheres), all three phases can coexist at equilibrium, each with a different value of density.

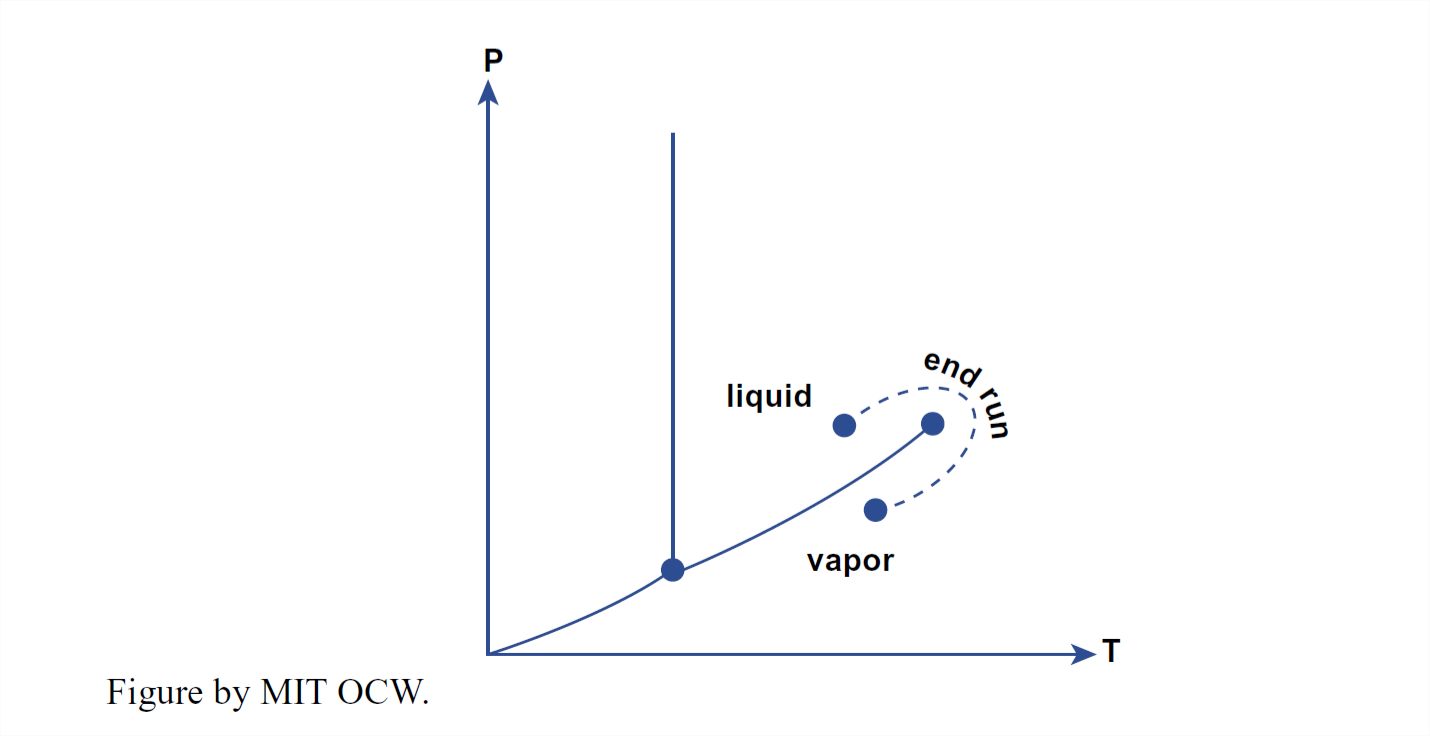
Another interesting thing about the P-T diagram in Figures 1-35 and 1- 36 is the narrowing and eventual termination of the vapor–water equilibrium cylinder as the phase boundaries join at what is called the critical point. This means that the distinction between the densities of liquid and vapor, which is great at the familiar Earth-surface temperatures and pressures, diminishes with increasing temperature and increasing pressure and finally vanishes at the triple point! At even greater temperatures and pressures, water exists in a single fluid phase, rather dense, with no distinction between the vapor state and the liquid state. (This is not relevant to this course, but I couldn’t resist including it, because it’s so fascinating—to science nerds like me, anyway.)

With reference to Figures 1-35 and 1-36, you can see that it’s possible to convert liquid water to water vapor continuously, without the catastrophic phase change involved in crossing the boundary directly by the shortest route. You could do this by changing the P–T conditions by a roundabout route like that shown in Figure 1-37. Along that route, all the properties of the water vary continuously from the liquid phase to the vapor phase.

Figure 1-35. P–T diagram for water in the region of the triple point.

Figure 1-36. Cartoon P–T diagram with axes distorted to show qualitatively both the triple point and the critical point clearly. (Not to scale!)

Figure 1-37. How you can pass from the liquid phase to the vapor phase, or vice versa, by continuous change in temperature and pressure around the critical point. (Not to scale!)

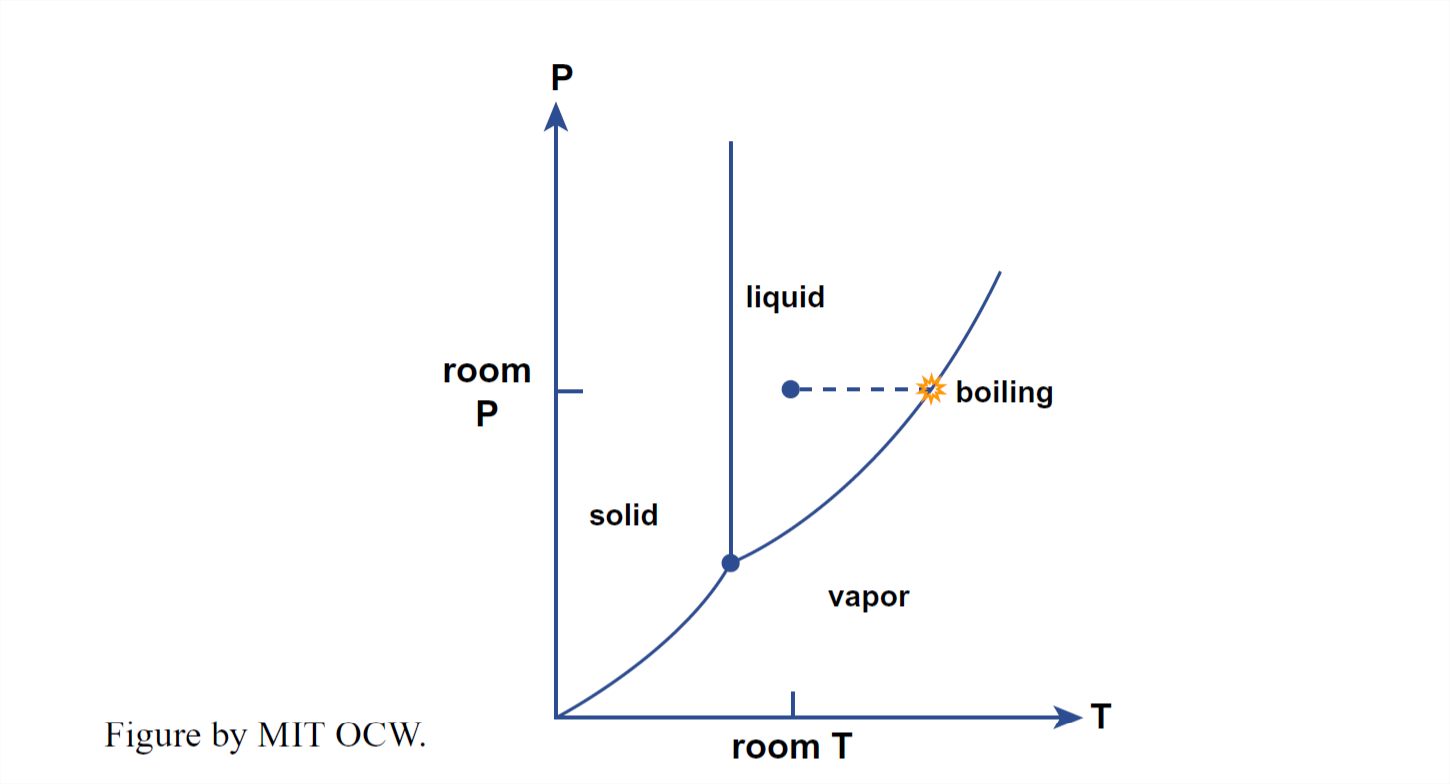
When you boil water, you are converting liquid water into water vapor. That process can be shown very simply on the P–T diagram for water (Figure 1- 38). You start with room-temperature water at atmospheric pressure (Point A in Figure 1-38). As you heat the water, it follows a path in the P–T diagram horizontally to the right, until it reaches the liquid–vapor phase boundary, whereupon it boils. The water then stays at the boiling temperature until all of the liquid water is used up.

You can also account nicely for the formation of dew and frost by use of the P–T diagram. In that case, however, you have to think more carefully about what to use for the pressure. The atmosphere consists of several gases, which together account for the atmospheric pressure, by virtue of their weight in the column of air that overlies the given locality. The contributions of each gas to the total pressure is called its partial pressure.

Water vapor in the atmosphere ranges in concentration from considerably less than one percent, in the coldest and driest air, to more than four percent, in the warmest and most humid air. In the P–T diagram in Figure 1-39, start with a point (Point A) well to the right of the liquid–vapor phase boundary, at a temperature above freezing. On a clear night, as the ground surface cools, by loss of heat by radiation to outer space, the water vapor takes a path horizontally to the left in the P–T diagram. When it reaches the liquid–vapor phase boundary it condenses as dew on the cold surfaces.

Figure 1-38. The boiling of water, as expressed in the P–T phase diagram for water.

Figure 1-39. The formation of dew and frost, as expressed in the P–T phase diagram for water.

You can do the same thing for the formation of frost, by starting at a temperature below freezing. Then the path leads horizontally left, from, say, Point B in Figure 1-39, to reach the ice–vapor boundary, at which point little ice crystals grow on the cold surfaces, fed directly from the water vapor in the air. (You can conclude from this that frost is not just frozen dew—although dew itself can freeze, as the air temperature decreases during the night.)

1.4.6 The Chemistry of Water

The water molecules in liquid water have a slight tendency to dissociate into H+ ions and OH- ions. The H+ ions are called (naturally!) hydrogen ions. They are basically just protons. (Actually, they tend to be hydrated by attachment to a water molecule, giving the formula H3O+, but conventionally they are written as, and treated as, just H+ ions.) The OH- ions are called hydroxyl ions.

This dissociation of water molecules into hydrogen ions and hydroxyl ions is expressed by the following simple chemical reaction, with which you are probably all familiar:

H2O⇔H+ +OH-

Keep in mind that, as with all such chemical reactions, water molecules are all the time dissociating into hydrogen ions and hydroxyl ions, while at the same time hydrogen ions and hydroxyl ions are recombining to form water molecules.

The balance between dissociation and recombination is such that only a very small proportion of the water molecules, at any given time, are dissociated.
In pure water that is contained in a completely insoluble container and is not in contact with any gas, proportion of water molecules that are dissociated at any given time is one in 107—a very small proportion. Moreover, the numbers of hydrogen ions and hydroxyl ions are equal, simply because the dissociation of one water molecule produces one H+ ion and one OH- ion. The concentrations of both the H+ ions and the OH- ions is said to be 10-7. (But beware: I am being somewhat superficial here because I am not telling you the units of the concentrations. That would take a lot more explanation than this course permits.)

If, now, we allow some H+ ions from outside to be added to the water, somehow, there will be a corresponding and one-for-one decrease in the numbers of OH- ions. Conversely, if we allow some OH- ions to be added to the water, somehow, there will be a corresponding and one-for-one decrease in the numbers of H+ ions. That leads to the idea of a scale of concentration of H+ ions. That scale is called the pH scale.

All of you probably have heard of the pH of aqueous solutions and know that it is somehow connected with the acidity of the water. The pH of an aqueous solution is defined as the negative of the logarithm to base ten of the concentration of hydrogen ions in the aqueous solution. (For those of you who are unfamiliar with the concept of logarithms, all you need to keep in mind that the base-ten logarithm of the number 107 is 7 and that the base-ten logarithm of the number 10-7 is -7). So the pH of pure water, in which, as discussed above, the hydrogen-ion concentration is 10-7, is 7. Aqueous solutions with greater concentrations of hydrogen ions have smaller pH values and are said to be acidic; aqueous solutions with lesser concentrations of hydrogen ions have larger pH values and are said to be alkaline.