1.3: Some Elementary Chemistry Relevant to the Earth's Surface
- Page ID
- 17406
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1.3.1. Atoms
Atoms are the building blocks of matter. Do I need to define for you what an atom is? One way of doing that is to say that an atom is the smallest unit of matter that reflects the chemical characteristics of the matter, in respect to its interactions with the atoms of other kinds of matter. In other words, atoms are units of matter that cannot be split up further without losing the chemical behavior of the matter, in terms of bonding with other atoms to form chemical compounds. If you’re going to understand why various kinds of atoms bond together the way they do to form the important minerals, you have to know what atoms are like and why the atoms of the various chemical elements behave differently.
The simplest cartoon for an atom (Figure 1-15) has a number of electrons orbiting a nucleus consisting of closely packed protons and neutrons.
Basic facts (don’t worry about how we know them, and don’t worry about remembering them for exam purposes):
- mass of proton: 1.7 x 10-24 g
- mass of neutron: 1.7 x 10-24 g
- mass of electron: about 1/1840 of the above electric charge on neutron: zero
- electric charge on electron (one “unit” of negative charge (smallest amount possible!)
- electric charge on proton: one “unit” of positive charge (just the opposite of that of the electron)
- size of atom: about 10-10 m size of nucleus: about 10-15 m
Note right away that for an atom to be electrically neutral is must have the same number of protons and electrons. So the nucleus is much heavier than the electron cloud around it, but also much smaller, by a factor of about 105.
What’s the best way for you to visualize the actual size of an atom? Think about the very tiniest dust particle you can see with your unaided eye under the best lighting conditions. Assume this to be one hundredth of a millimeter, or 10-5 m. About how many atoms would stretch across that distance? See Figure 1- 16 for a computation.

What are electrons really like, and what are their orbits around the nucleus really like? These are complicated questions, difficult to answer in a simple way. To get a good idea you need to know something about quantum mechanics, a branch of physics, which has grown up since the early decades of the Twentieth Century, that deals with the behavior of very small particles.
Particles that are very small and very fast-moving behave in ways our common sense doesn’t cover. Electrons aren’t just little solid spheres, like billiard balls or mini-planets; they are both particles and little packets of waves at the same time, in that in some ways they behave like particles and in other ways they behave like waves. In this respect, electrons are just like light, which also shows this particle–wave duality. If this doesn’t make much sense to you, don’t worry about it. Also, we have no way of knowing where the electrons are in their orbits around the nucleus: all we can say is what the probability is that they will be found in a given place. So it’s a little better to cartoon the atom as a smeared-out “probability cloud” of electrons around the nucleus (Figure 1-17), although even that is still not very satisfactory.

But with all this said, in order to get somewhere studying minerals we will make some simplifications about electrons and think of them as “ordinary” little particles traveling in “ordinary” little orbits around the nucleus.
1.3.2. The Chemical Elements
There are many different kinds of atom, depending upon the number of electrons, protons, and neutrons in the atom. In terms of the chemical behavior of atoms, which is what we’re interested in here, the important thing is the number of electrons (and the equal number of protons), because that’s what determines how the atom bonds (or fails to bond) with other atoms. Each distinctive kind of atom, in terms of the number of electrons and protons it has, is called a chemical element (or just an element).
Let’s investigate the structure and behavior of the elements by starting with the lightest and simplest kind of atom: hydrogen. The nucleus of the hydrogen atom consists of one proton, and the electrically neutral atom has one electron orbiting the proton nucleus. The next lightest and next simplest atom is helium. Its nucleus consists of two protons, and the electrically neutral atom has two electrons orbiting it—et cetera. We can build up a picture of all of the elements in this way, by adding one proton (and therefore one electron) at a time—with some neutrons thrown into the nucleus also.

Figure 1-18 is a chart of the first twenty or so elements. This covers most of the important elements that go into the most important rock-forming minerals. Why have I arranged the elements in this way? You might remember from some chemistry course that this represents the first three rows of what is called the periodic table of the elements, plus a little of the fourth row.
This grouping of the elements corresponds very closely to the chemical behavior of atoms of these elements, when it comes to combining, or bonding, with atoms of other elements to form chemical compounds. (Remember that minerals are just chemical compounds.)
This kind of grouping (more complete than shown here) was first perceived by the Russian scientist Dmitrii Mendeleev in 1869. His insight into the nature of organization of the elements in terms of their chemical behavior paved the way for people after him to actually discover new elements his table predicted. It was not until the early 1900s, with the advent of the quantum theory of matter, however, that people realized why the elements are arranged in this way.
Electrons are present in atoms in group of orbits called shells. That is, electron orbits occur in groups. A filled shell (all the electron orbits of the shall are occupied by electrons) is a very stable configuration of electrons—stable in the sense that the electrons are tightly bound, and it takes a lot of energy to remove one, and also the atom has no tendency to take on electrons to try to fill a shell. Elements with filled-shell electron configurations are very inert and almost totally nonreactive.
The first shell has positions for two electrons. This corresponds to the first row of the periodic table. Hydrogen doesn’t have a filled-shell configuration, so it enters into an enormous number of chemical compounds in its search for the extra electron, from some other atom willing to give it up, to attain the filled-shell configuration. But helium, which has two electrons already, is an inert gas. The second shell contains eight electrons, corresponding to the second row of the periodic table. Neon has both of the first two shells filled and, like helium, is an inert gas. The third shell also contains eight electrons, and corresponds to the third row of the periodic table. Argon is the inert gas with all three first shells filled.
1.3.3. Ions
How about the elements with unfilled shells? There is a strong tendency for an atom to end up with a filled shell, by either giving up electrons (to another atom) or taking on electrons donated from another atom (or by sharing electrons with another atom; see below). Atoms that have attained a filled-shell configuration by either giving up or taking on electrons are called ions. The characteristic thing about ions is that have an electric charge.
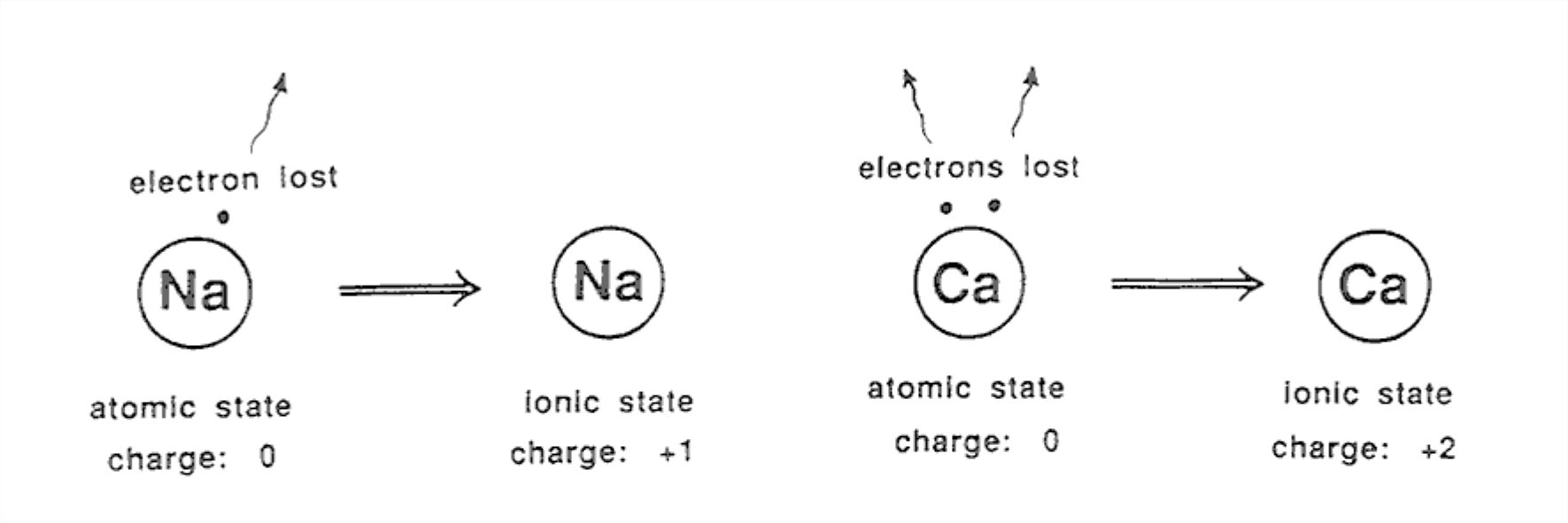
Those elements (near the left side of the periodic table) with only a few electrons in their outer shell can fairly easily be stripped of those electrons so as to have a filled-shell configuration. Examples are sodium (Na), magnesium (Mg), potassium (K), and calcium (Ca). Ions like these have a positive charge, because they have lost electrons (which are negatively charged).
Na atom minus 1 electron → Na+ ion (single positive charge)
Mg atom minus 2 electrons → Mg2+ ion (double positive charge)
Figure 1-19 shows some examples of positively charged ions.
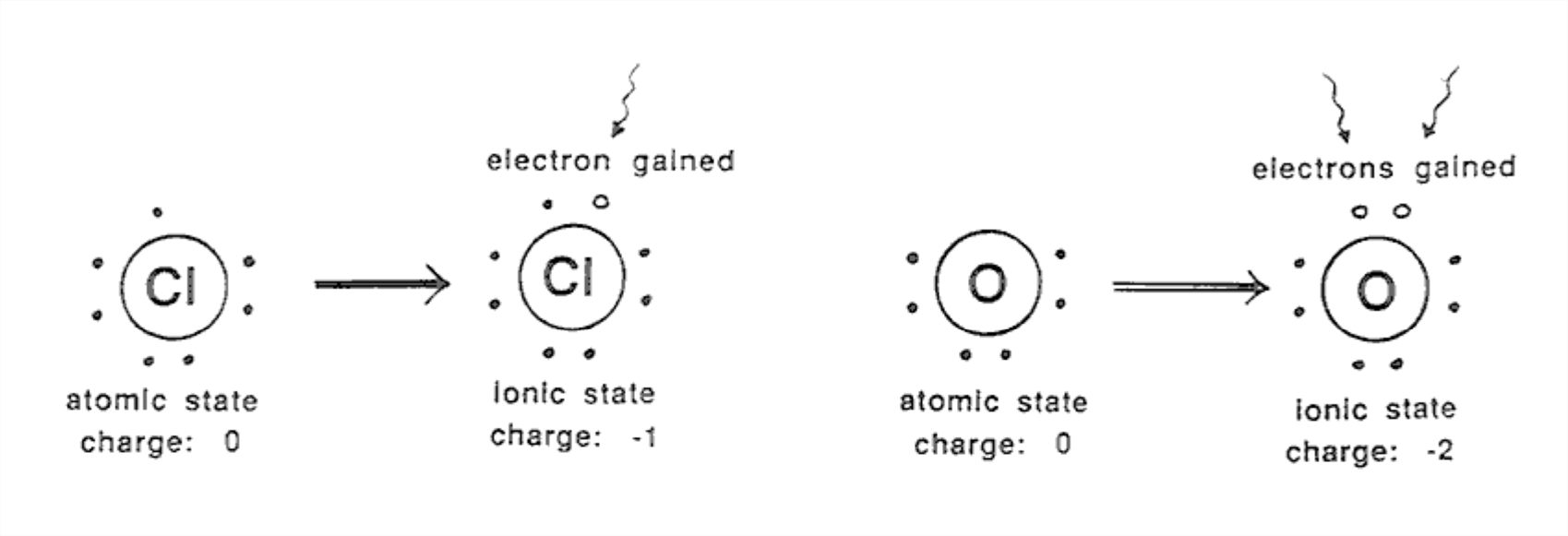
Elements that are near the right side of the periodic table, with almost enough electrons in the outer shell to produce a filled-shell configuration, can easily take on enough electrons to fill the shell. Examples are oxygen (O), fluorine (F), sulfur (S), and chlorine (Cl). Ions like these have a negative charge, because they have gained electrons.
Cl atom plus 1 electron → Cl- ion (single negative charge)
O atom plus 2 electrons → O2- ion (double negative charge)
Figure 1-20 shows some examples of negatively charged ions.
For reasons that need not concern us here, positively charged ions are called cations and negatively charged ions are called anions.
1.3.4. Ionic Bonds
All of you know that there are such things as electric charges and that these can be moved around from place to place. (Think about hair and clothes on dry days. Or get under the synthetic-fiber bedspread in the dark when the humidity is low and run your hands over its surface, and watch the sparks.) Benjamin Franklin recognized that there can be positive and negative charges (incidentally, the assignment of “positve” and “negative” is arbitrary) and that charges of the same sign repel one another and charges of opposite sign attract one another. This is expressed by Coulomb’s law, one of the basic laws of physics:
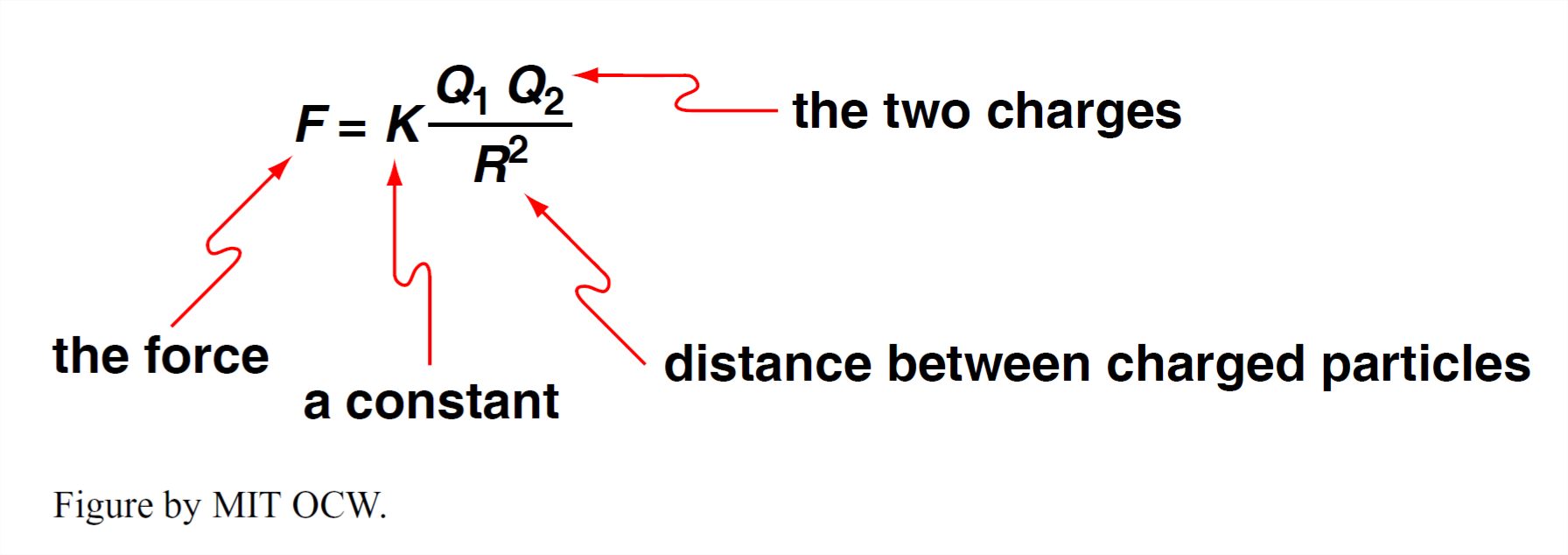
- If Q1 and Q2 are of the same sign, F is repulsive
- If Q1 and Q2 are of opposite sign, F is attractive
All of this applies to ions! Two ions of opposite charge can become bonded to one another by this Coulomb attractive force. This kind of bond is called an ionic bond. Most minerals are held together by just this kind of bond. (Now we’re getting somewhere on the basic nature of minerals.) Crystals that are held together by ionic bonding are called ionic crystals.
1.3.5. Ionic Crystals
The mineral halite (NaCl, sodium chloride, also known as table salt) is a good example of an ionic crystal—and an important rock-forming mineral as well. The structure of halite involves equal numbers of positive ions (sodiums) and negative ions (chlorides) arranged in a cubic array, each sodium surrounded by six chlorides and each chloride surrounded by six sodiums. (See Figure 1-21.)
Think of three mutually perpendicular lines, and along each line there’s a regular alternation of sodium and chloride ions. If you draw lines connecting all of the six chlorides that are the nearest neighbors to any given sodium, you get a regular geometric solid, called an octahedron, made up of eight equilateral triangles. For this reason we say that there is octahedral coordination of chlorides around sodiums. You can show for yourself that the same holds true for the six nearest-neighbor sodiums around any given chloride.
The picture in Figure 1-21 is in one sense a fake, because, for reasons of good visibility, I’ve drawn it with too much space between adjacent ions. To get the “true” picture you have to imagine that all of the spheres, of both kinds, expand (in such a way that the relative sizes of the two kinds stay the same) until they are all in contact; this is difficult for me to draw intelligibly.
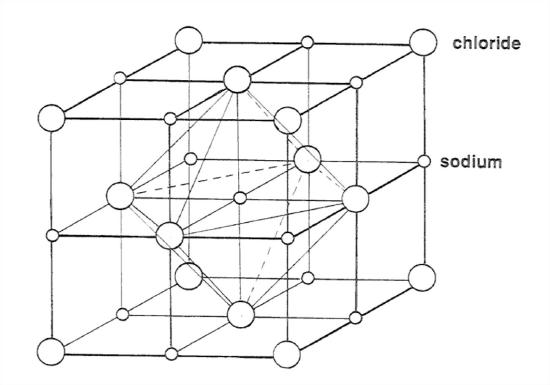
It turns out that the relative sizes of Na and Cl ions are just about right for this kind of “cubic” packing—just right in the sense that they all come out to be just about touching. In fact, if they were of different relative sizes the packing would have come out to be of some different kind.
Look at the central sodium in the figure. The strongest forces on it are attractive, exerted by its six nearest neighbors, which are chlorides. (Keep in mind the strong, inverse-square dependence of the force on the separation distance in Coulomb’s law.) The next strongest forces are repulsive, exerted by its twelve next-nearest neighbors, which are sodiums. And so on outward. The structure likes to form because the overall picture of forces, summed over all of the ions, near and far, surrounding that ion is attractive. Other structures with different kinds of atoms, which might seem okay at first thought, don’t form because the overall picture of forces comes out to be repulsive. To get such a structure to hold together, you would have to deep squeezing it hard from all directions.
There are two other factors that determine whether a given mineral forms (i.e., is stable) in a given situation:
• All atoms are in a state of continual jiggling, because of their thermal energy. Only at absolute zero does all movement cease. This jiggling may be so strong that, even though the picture of inter-ionic forces is attractive, the crystal flies apart because of the thermal jiggling. This is why crystals (ice is an everyday example) melt as the temperature rises.
• The greater the concentration of Na and Cl ions in the medium surrounding the crystal, the higher the temperature at which the crystal melts, because ions from the surroundings tend to diffuse into the crystal and keep it together.
1.3.6. Covalent Bonds
There’s another kind of bond that’s especially important in silicate minerals, called a covalent bond. It’s not as easy to understand than the ionic bond. Atoms can fill their electron shells by sharing electrons with other atoms.
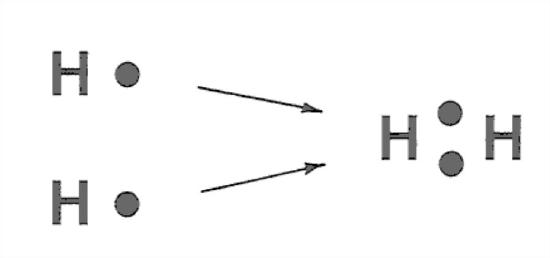
The simplest example is the bond in the H2 molecule (Figure 1-22). This is very schematic, and it doesn’t give you a good picture that both electrons orbit both nuclei. It’s as if each nucleus gets something for nothing. Figure 1-23 is a slightly better way of looking at it, in terms of the shape of the electron cloud.

Comments:
- Covalent bonds (if they are favorable in the first place because of electron-orbit considerations) tend to be found between atoms of elements that are in the same or almost the same position in the periodic table, in terms of columns.
- Many bonds are purely ionic or purely covalent, but many are intermediate in character: there is partial sharing of electrons, but the density of electron distribution is shifted so that one component atom tends to be negatively charged and the other positively charged. This is called partial ionic character of the bonds.
- Covalent bonds are inherently more complicated to understand than ionic bonds, and I’ve been much more superficial about them. They depend upon certain intricacies of electron orbit structure that are understandable only on the basis of quantum mechanics. Covalent bonds actually have a directional property that’s governed by the nature of electron distributions around the atoms, not just packing geometry as in the case of ionic bonds. It’s as if the atoms had little hooks on them in certain positions.
1.3.7. Solids, Liquids, and Gases
Most chemical compounds can exist in all of three different states of aggregation—as a solid, a liquid, or a gas—depending on temperature and pressure. This was known, of course, long before the molecular theory of matter was developed in the late eighteenth century and the early nineteenth century. In the past hundred and fifty years, great effort has gone into developing theories to account for the nature of solids, liquids, and gases on the molecular level. (Here, I'll use the term molecule for atoms, ions, or molecules indiscriminately.)
You probably already know well the fundamental macroscopic distinctions among gases, liquids and solids:
gas:
• has relatively low density
• cannot withstand applied shearing forces without continuing deformation
• expands to attempt to fill its container uniformly
liquid:
• has relatively high density
• cannot withstand applied shearing forces without undergoing continuing deformation
• maintains a definite volume within a well-defined bounding surface 32
solid:
• has relatively high density
• withstands applied shearing forces without undergoing continuing deformation
• maintains a definite volume within a well defined bounding surface
On a more fundamental level, the basic picture of a gas is that its constituent molecules are widely separated relative to their diameter, except for occasional close encounters, and are moving in free trajectories with only occasional collisions with the walls of the container and with each other. If you could somehow travel on a gas molecule, most of the time you would be having a boring ride, because the molecule would be in a state of uniform straight-line motion at constant speed, with neighboring molecules so far away you’d have to use binoculars to see them. Every now and then, however, another molecule or the wall of the container would come rushing toward you, and your molecule would rebound elastically from the encounter.
This state of motion, with its well-defined elastic collisions and negligible mutual forces among molecules in the meantime, lends itself to successful modeling of the gaseous state—especially because many-body (that is, three-plus) collisions or interactions are so rare. Such modeling has led to the kinetic theory of gases, by which most of the properties of gases can be accounted for or predicted.
At the other end of the line, on a molecular level a solid is characterized by fixed and ordered positions of the constituent molecules, with packing so close that there are strong forces at all times between any given molecule and all of its near neighbors. At temperatures above absolute zero the molecules oscillate or vibrate in various ways about their fixed mean positions, but only rarely do molecules trade places in their ordered arrangement.
If you could occupy one of the molecules in the solid structure, you would feel as if you had been consigned forever to one of those vibratory-massage beds they used to have in motels, and if you looked over at the strictly regular pattern of neighboring molecules looming near you, they would be vibrating too, but maintaining their mean positions for extremely long times before trading places with a neighbor. And you would have the same picture for as far as you could see through the structure.
Despite the complexity of the mutual forces, the ordered and permanent arrangement in crystalline solids has allowed successful modeling, and the solid state is by now well understood.
Liquids, however, have presented much greater problems than gases and solids. As with solids, the molecules are always close enough together that they exert strong forces on one another, but the degree of ordering (or, more precisely, the time scale for the existence of ordering) is much less than for solids.
If you were to occupy a molecule in a liquid, your vibratory movement would be about the same as when you were in the solid, and your neighbors would loom almost as close. But the arrangement of your neighbors would stay the same only for a short time and then change to some different arrangement by a combination of just shifting in position and actually trading places. You might or might not get a sense of regular arrangement of the neighbors, but even if you did you wouldn’t be able to follow that regularity very far outward, and anyway it would be transitory.
Various kinds of conceptual models of the liquid state, partly geometric and partly kinematic, have been devised. These models can be massaged, by supplying somehow the constants or parameters that must go along with them, to predict the properties of the liquid. None of these models comes close to accounting well for all of the important properties of liquids. Knowledge of the liquid state is therefore still far from perfect.
1.3.8. Chemical Reactions
In case your knowledge of chemistry is scanty, here is some basic stuff. Chemical reactions, like Reaction 1 above, are processes by which certain substances react with one another to produce other substances. (That includes situations in which a single substance undergoes a change by which it is transformed into one or more different substances, or by which two or more substances are transformed chemically into a single substance.) The beginning substances are called the reactants, and the ending substances are called the products. The substances involved might be solids (crystalline or amorphous), or ions or molecules dissolved in a liquid medium, or even just the atoms and molecules of a gas.
The details of chemical reactions involve usually complex interactions among the atoms that constitute the substances involved, and they need not concern us here. In the case of solid substances, you can think in terms of the atoms of the reactants being disengaged from the crystal structure of the reactant(s) and then added to the crystal structure of the product(s). Or, in the case of the dissolution of a solid substance in a liquid, what’s going on is that the ions or molecules of the solid are being detached from the surface of the solid, to roam around freely in solution in the liquid. The reverse of a dissolution reaction like that is the addition of the dissolved ions or molecules onto the growing surface of the solid by removal from solution—a process called precipitation (not to be confused with the meteorological term, which is used for liquid or solid water particles falling through the atmosphere).
In the case of dissolution or precipitation, mentioned above, what’s really going on is that ions or molecules are continually being added to and removed from the solid surface. Whether the solid is shrinking (dissolution) or growing (precipitation) depends on the relative rates of removal and addition of atoms or molecules.
Chemical reactions can go both ways. That’s why Reaction 1, shown above, has the double arrow in the middle of it. If you pump up the concentration of the substances on the left side of the reaction, that drives the reaction to the right, producing the substances on the right (then called the products) at the expense of the substances on the left (then called the reactants). But if instead you pump up the concentration of the substances on the right, that drives the reaction to the left—and then you have to use the terms “reactant” and “product” in reverse!
1.3.10. Oxidation
The business about oxidation, and the difference between iron in the ferrous state and in the ferric state, is likely to be mysterious to you unless you have some sophistication in chemistry. Here’s some background material on such matters. You probably have heard of oxidation, and you may also have heard of reduction. These two processes go hand in hand, and are often combined into the term redox.
Many chemical reactions we deal with in and on the earth involve transfer of the actual nuclei of the atoms involved. The dissolution and precipitation of soluble salts like NaCl are good examples. A large and important class of chemical reactions, however, involve only transfer of electrons. This is the stuff of a field of chemistry called electrochemistry. The practical applications of electrochemistry include batteries, electrical smelting of ores, and electroplating of one metal upon another.
A simple example should help to give you the basic idea. Suppose you mixed up an aqueous solution that contains ferric ions, Fe3+, and another solution that contains stannous ions, Sn2+. (Iron can exist in solution as two kinds of ions, with different electric charges: ferric ions, Fe3+, and ferrous ions, Fe2+; tin can exist in solution as two kinds of ions also: stannic ions, Sn4+, and stannous ions, Sn2+). If you then mix the two solutions together, the Fe3+ ions take electrons away from the Sn2+ ions, and in the process they become Fe2+ ions and make the Sn2+ ions into Sn4+ ions. (Remember that, by convention, electrons have a unit negative electric charge.)
The Fe3+ ions have stolen electrons from the Sn2+ ions. Why? A “deep” answer would require a lot of explanation, but an adequate (“shallow”) answer here might be that the details of the electron structure of the two kinds of ions makes that “want” to happen, and so it does, spontaneously. The chemical reaction can be written, simply, as
2Fe3+ + Sn2+ → 2Fe2+ + Sn4+
The reaction proceeds until all of one or the other reacting ions gets used up.
If you made up two separate aqueous solutions, one containing Fe3+ ions and the other containing Sn2+ ions, and then connected them with a conducting wire, electrons would flow from the one with the Sn2+ ions to the one containing the Fe3+ ions, to make the reaction happen, even though the two kinds of ions are not in contact! You could then measure the voltage on the wire, at the start of the process. The voltage is a measure of what is called the electrical potential between the two solutions. Think of voltage as an “electrical pressure”, analogous to the water pressure that drives the flow of water in your home water pipes.
It would be nice to be able to measure, separately, the electrical potential associated with the removal of electrons from the Sn2+ ions and the addition of electrons to the Fe3+ ions. You can think of those two processes as “half- reactions”, which add together to produce the whole reaction, written above. You could then use such results to figure out, directly, which substances steal electrons from which other substances.
Unfortunately, there’s no way of doing that: all you can do is measure the electrical potential associated with the whole reaction. Chemists have gotten around that problem in a neat and convenient way: they characterize reactions of the kind described above that involve a wide variety of different substances with reference to a solution that contains molecular hydrogen (which could be bubbled, as a gas, through an aqueous solution). To make that concrete, you can imagine putting either the Fe3+ ions or the Sn2+ ions into a solution into which molecular hydrogen is added. The electrical potential of the reaction that takes place (called the redox potential, denoted by Eh) can then be measured. Then they tabulate all of the half-reactions relative to the hydrogen standard.
Substances, like oxygen, that tend to steal electrons away from other substances are called oxidizing agents; substances, like metallic iron, that tend to lose electrons to other substances are called reducing agents. The word “oxidizing” here, however, is misleading, because a great many other substances can act as oxidizing agents, in the sense that they tend to steal electrons away from other substances. The rationale, I suppose, is that oxygen is the most important oxidizing agent in so many natural chemical systems. Likewise, there are many other reducing agents besides metallic iron, but because iron and its compounds are so important in natural chemical systems, it’s natural to think in terms of metallic iron, or ferrous iron ions (Fe2+), as reducing agents.
Finally, here are some comments on oxygen vs. the two kinds of iron ions. In a solution containing oxygen, ferrous (Fe2+) ions are inevitably oxidized to ferric (Fe3+) ions, which have a strong tendency to combine with oxygen to form insoluble ferric iron oxides or hydroxides. If, on the other hand, the solution has no free oxygen (perhaps all of the available oxygen had already been used up in the oxidation of organic matter, which is a reducing agent), then the ferrous ions (Fe2+) remain happily in the solution.

