1.1: Some Basic Physics Relevant to The Earth's Surface
- Page ID
- 17404
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)BACKGROUND: SOME BASIC (NON-MATHEMATICAL) PHYSICS RELEVANT TO THE EARTH’S SURFACE
1. Energy
First you need to feel comfortable about the nature of energy. We have to be concerned with three forms of energy: energy of motion (called kinetic energy), energy of position (called potential energy), and energy of thermal motions of atoms of molecules of a material (called thermal energy or heat energy). Kinetic energy and potential energy together are often referred to as mechanical energy.
If you are not already familiar with these concepts of energy, here’s a little demonstration that should serve the purpose of giving you the basic ideas. You will need a lump of modeling clay or putty. Throw the lump straight up in the air. When it leaves your hand, it has a certain speed and therefore a certain kinetic energy. It’s slowed by the downward force of gravity as it rises, so it loses kinetic energy, but that lost kinetic energy is stored as energy of position, by virtue of being located higher up in the gravity field of the Earth. When it reaches the top of its trajectory, all of its kinetic energy has been stored as potential energy. Then on the way down, the stored potential energy is converted back into kinetic energy. If you were doing this in a vacuum in some enormous evacuated bell jar or on the surface of the Moon, the putty would have the same speed when it lands back in your hand as when you threw it upward. The mechanical energy of the lump, kinetic plus potential, is the same all along the trajectory; the mechanical energy is said to be conserved.
On the real surface of the Earth, of course, the lump is bathed in air, and its motion is retarded by friction both on the way up and on the way down. That friction warms the lump (and the air it passes through), slightly, converting some of the mechanical energy into thermal energy.
Another thing you can do with the lump is drop it on the floor from some high place. It has some kinetic energy as it lands on the floor, but then it comes to a stop upon impact, without even rebounding. What happened to all of its kinetic energy? It was converted entirely to thermal energy, via the friction involved in the deformation of the lump as it made impact. If you had the right equipment you could actually verify for yourself that the lump was warmer after it landed than before.
2. Electromagnetic Radiation
All bodies (pieces or regions of matter, in the physicist’s parlance) at temperatures above absolute zero radiate energy in the form of electromagnetic waves. The subject of electromagnetism goes to the heart of physics, and it’s much too complicated for a full treatment here, but all of you are familiar with the existence and effect of electromagnetic waves, in various ways: the radiant heat you receive from your fireplace or electric heater; the light you perceive with your eyes; radio, television, and radar waves; x rays.
Electromagnetic waves vary over an enormous range of wavelengths, from the very short wavelengths of cosmic rays and x rays, through the intermediate range of ultraviolet and visible light, down through the infrared to the long wavelengths of radio waves and the like (Figure 1-1). The shortest wavelength visible to the eye, at the edge of the ultraviolet, is about 0.36 μm; the longest wavelength, at the edge of the infrared, is about 0.76 μm.

Of the various physical laws governing the emission and absorption of electromagnetic radiation, the one that’s most relevant for us here is Wien’s law: the product of the absolute temperature and the wavelength of the most intense radiation is a constant. That means that a body with a relatively high surface temperature, like the sun, radiates energy at relatively short wavelengths, and a body with a relatively low surface temperature, like the earth, radiates energy at relatively long wavelengths. The maximum intensity of the Sun’s radiation is at about 0.5 μm, whereas the maximum intensity of the earth’s long-wave radiation is at about 10 μm, well into the infrared range.
But bodies like the Sun and the Earth don’t radiate all of their energy at a single wavelength: they radiate over a wide range of wavelengths. Figure 1-2 is a graph of the intensity of solar radiation as a function of wavelength. We see from Figure 1-2 that the sun radiates most of its energy in the visible and ultraviolet part of the spectrum, but a substantial part also in the infrared part of the spectrum. A similar graph for the Earth’s radiation back to space, also shown in Figure 1-2, would show a similar shape but shifted far toward the long wavelengths.
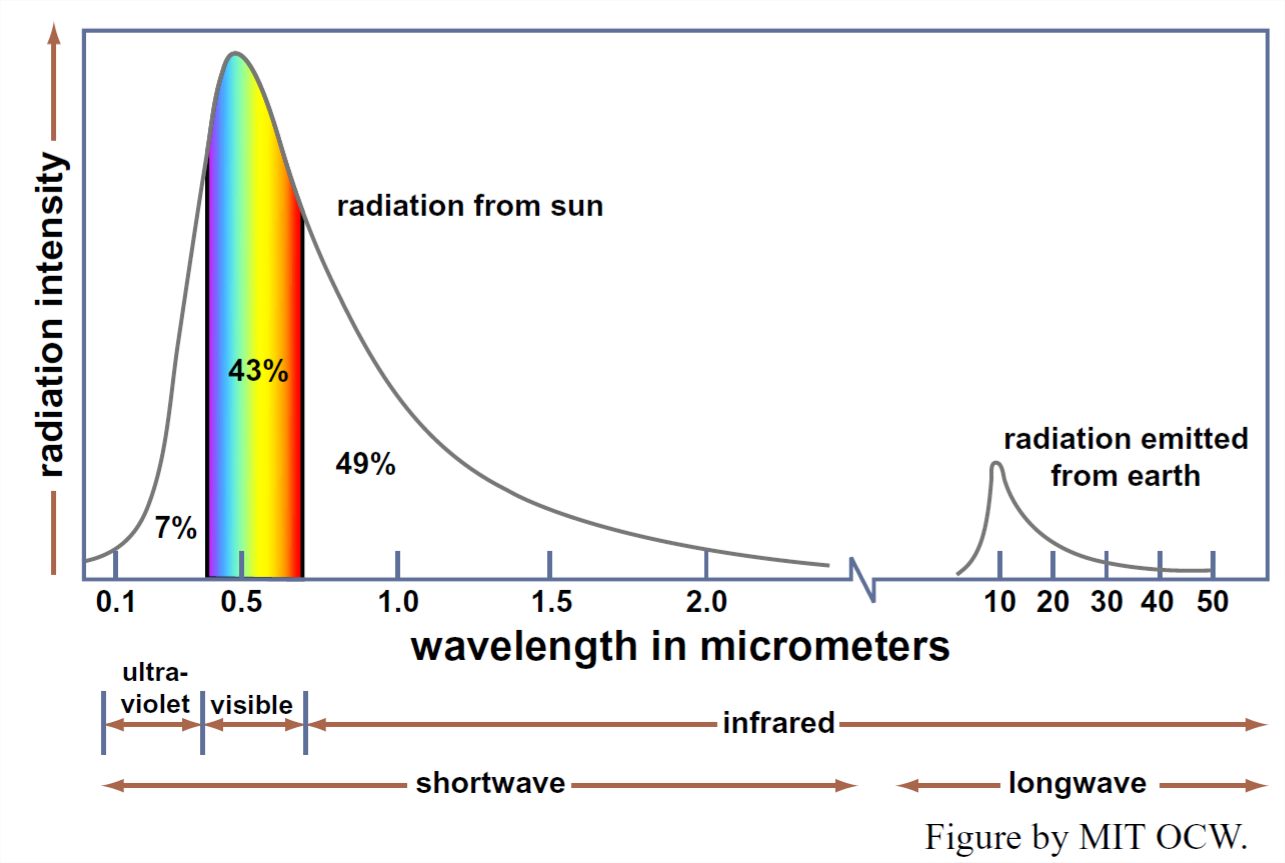
The next time you are out in your yard or garden, or in the park or the countryside, I want you to think about long-wave radiation: you can’t see it (although you can feel it), but it’s operating everywhere, all the time, and it’s as important as sunlight in terms of its effect upon local climate (although obviously not in terms of plant growth, or suntanning, or skin cancer).
Temperature and Heat
All of the atoms or molecules of matter undergo inherent motions. In gases, these motions consist in long, straight trajectories of the atoms or molecules, called free paths. If the gas is enclosed in a container, the particles collide with the walls of the container. Macroscopically we sense the aggregate of such collisions as the pressure that the gas exerts on the walls of the container. Now and then, the particles also collide with one another as they fly about. The average distance traveled by a particle between collisions with other particles is called the mean free path. The mean free path of air molecules at atmospheric pressure and a temperature of 0°C is about 2 x 10-5 cm (a very small distance, equal to about one thousand molecule diameters). The collision frequency is about 5 x 109 per second, which is an extremely short time. Each molecule makes about five billion collisions per second!
In solids, the atoms or molecules are fixed in place, either in the regular array of a crystal structure or in the irregular arrangement of an amorphous (noncrystalline) solid. You will learn more about that in Chapter 2. But the particles do not stand still: they vibrate in place, with a certain amplitude and frequency. In liquids, the atoms or molecules are in close association with one another, and they exert strong forces on one another, but they too undergo the same small-scale random motions that are characteristic of gases and solids.
What we are dealing with here are called thermal motions, or thermal vibrations. These motions are an inherent feature of all matter. The moving or vibrating particles have some energy of motion, called kinetic energy. The hotter the matter (that is, the higher the temperature of the matter), the more vigorous or energetic are the thermal motions. In fact, what physicists call the temperature of the matter is just a measure of the average kinetic energy of all of the constituent atoms or molecules. As the temperature of a body of matter is lowered, a point is reached at which the thermal energy of the atoms and molecules is at an absolute minimum. That temperature is called absolute zero, about -273°C.
All of you know about the Fahrenheit scale of temperature, which we here in the United States use in our everyday lives. You probably also know that it has been supplanted in most other parts of the world, and by scientists everywhere, by the Celsius scale of temperature (earlier called the centigrade scale), with the freezing point of water at 0°C and the boiling point of water (at sea-level pressure) at 100°C. What may be less familiar to you is the Kelvin scale of temperature, in which the degrees are the same as in the Celsius scale but zero is fixed at absolute zero. In the Kelvin scale, the degrees are called kelvins (not “degrees Kelvin”).
It’s important for you to understand the distinction between temperature and heat: they are related, but they are not the same! Heat is the total internal energy of all of the constituent atoms or molecules in a given body of matter. (By internal energy here, I mean all of the kinetic energy of the atoms and molecules, which is discussed in the preceding paragraphs, together with the energy associated with the forces of attraction among the individual atoms and molecules.) Other things being equal, the bigger a body of matter, the more heat it contains. That’s in contrast to the temperature of the body, which, as you learned above, is a measure of the thermal energy of the individual atoms or molecules.
In contrast to heat, the temperature of the body of matter is independent of how big the body is. Here is an everyday example of this: a small pot of water at nearly 100°C on the stovetop is much hotter (that is, has a much higher temperature) than the water in your almost-full bathtub at 40°C, but the total heat content of the water in the bathtub is much larger than the total heat content of the water in the pot.
Various units are used to describe heat. The two that are in common useinphysicsarethecalorie,whichisdefinedastheamountofheatthat’sneeded to raise the temperature of one gram of water by one degree Celsius. Incidentally, there is a lot of potential confusion about calories. What I defined above is sometimes called the gram calorie, abbreviated as “cal”. There is also the kilogram calorie (the amount of heat it takes to raise one kilogram of water by 1°C), abbreviated as “Cal”. There are one thousand gram calories (“small calories”) in one kilogram calorie (“large calorie”). The calorie that’s used to measure the energy content of foods—that is, the dieter’s calorie—is the same as the kilogram calorie.
Heat is also measured in joules, the unit of energy in the mks (meter, kilogram, second) system of units in physics. The joule is named in honor of James Prescott Joule, a British physicist (1818–1889), who was the first to demonstrate the equivalence of heat and mechanical energy by means of a classic experiment in which he increased the heat content of water in a large vat by adding mechanical energy to the water by stirring it with a paddle. One gram calorie is equal to about 4.18 joules. Just to confuse you further, in everyday life it’s common to measure heat in terms of British thermal units (Btu). One Btu is the amount of heat needed to raise one pound of water one degree Fahrenheit (technically, from 63° to 64°). One Btu is about equal to 250 gram calories.
Finally, the concept of heat capacity is an important for anyone who thinks about the Earth’s surface. The specific heat capacity of some given material is the amount of heat that has to be added to a unit mass of that matter to raise its temperature by one unit. This could be expressed, for example, as joules per kilogram or as calories per gram. The importance for the Earth’s surface is that the rocks, soil, and waters of the surface all have their own specific heat capacities, so it takes certain amounts of incoming solar energy to raise their temperature, and certain amounts of outgoing terrestrial long-wave radiation to decrease their temperature. Water has a much greater (I’m tempted to say spectacularly greater) specific heat capacity than the multifarious solid materials of the surface. That causes regions that are dominated by the oceans to have much more equable climate, other things being equal, than regions far removed from the oceans.
How Heat Is Transported
So far we’ve dealt only with radiation. Heat can also be transported by conduction, convection, and advection.
Conduction of heat through a solid is familiar to all: the handle of the pan on the stove heats up by conduction from the hot body of the pan. The same holds true for liquids and gases, although in that case conduction is often overwhelmed by the more efficient processes of convection and advection, by which the fluid, carrying its heat, is moved bodily from place to place.
The principle behind heat conduction is simple. The heat of a body is a manifestation of the thermal agitation of the constituent atoms and molecules. The hotter the material, the more energetic are the thermal motions of the atoms and molecules. When a difference in temperature from one place to another is imposed upon the body, the differing “intensity of jiggling” of the atoms and molecules from place to place is evened out, thus equalizing the temperature. We say that heat has been transported from the region of higher temperature to the region of lower temperature.
Convection is the term used for the circulation of a fluid driven by differences in density brought about by differences in temperature. The familiar example is a room warmed by a radiator on a cold winter day (Figure 1-3): the heating of the air by the radiator decreases its density, causing it to rise, and as it is cooled by the cold walls of the room, it sinks and takes a return path to the radiator, again to be heated. Convection cells of this kind are extremely important in atmospheric processes, on both small and large scales.
The horizontal motion of fluid from one region to another, driven by horizontal differences in atmospheric pressure, is called advection. One can sense the importance of advection on a gloomy winter day when a warm wind blows from the south, melting much of the snow cover. Of course, what a local observer senses as advection might just be one very small part of some gigantic convection cell.
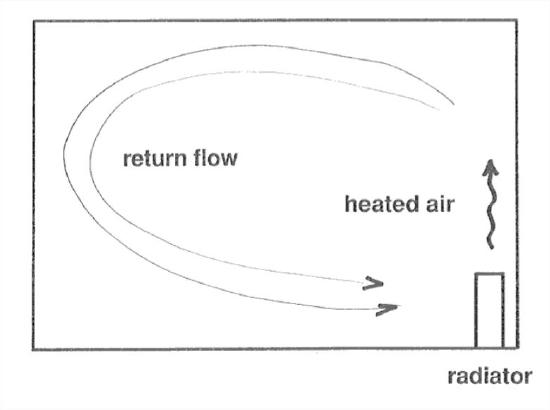 Figure 1-3. A convection cell.
Figure 1-3. A convection cell.
