8.5: Deltas

Introduction

A delta is a body of sediment deposited at a point along a body of water where a sediment-transporting channelized flow of water enters the water body. Deltas range in size from those little decimeter-scale bodies that you can see forming when a rivulet of rainwater enters a puddle during and right after a rain, to giant bodies at the mouths of major rivers like the Mississippi. The reason deltas form—and I suppose that this is obvious—is that as the channel flow enters the water body it spreads out and thereby decelerates, dropping much of its sediment load at or not far from its mouth.

The concept of a delta is simple, but the geometry of large deltas in the real world is rather complicated and highly varied, owing to a variety of factors. More on that later; first, some material on the hydrodynamics of deltas.

The Hydrodynamics of Deltas

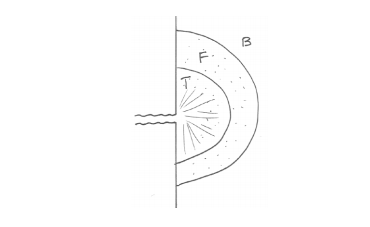
To understand deltas, you need to know something about jets. In fluid dynamics, a jet is a fluid motion created where a high-speed flow in a pipe or other conduit enters a large body of relatively still fluid. It’s easy to visualize the classic jet (Figure 8-35). A pipe enters a large tank of still water. When the water flowing in the pipe enters the tank, it no longer feels the force (the downstream pressure gradient) that was driving the flow in the pipe. Its momentum carries it out into the water of the tank, but friction with the surrounding fluid robs it of its momentum, and it eventually slows to a stop. Most such jets are turbulent—unless they are very small, very slow, and/or consist of very viscous fluid—and the mixing of eddies at the margins of the jet entrain ambient water into the jet, causing it to widen.

Figure 8-35. A jet entering a body of still fluid from a pipe. This is a cross-section view, cut through the axis of the pipe flow and the jet.

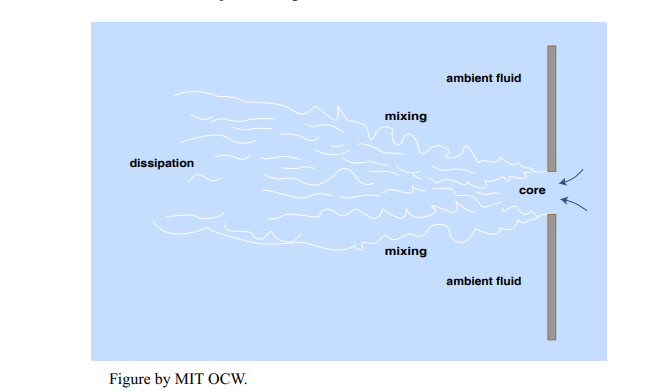
As you can imagine, the mixing at the margin of the jet tends to even out the properties of both the jet and the ambient fluid—which might be temperature, salinity, or concentration of suspended solids. Note in Figure 8-35 that there is a residual core in the jet, which has not yet been affected by the marginal mixing. This core shrinks to nothing in the downstream direction.

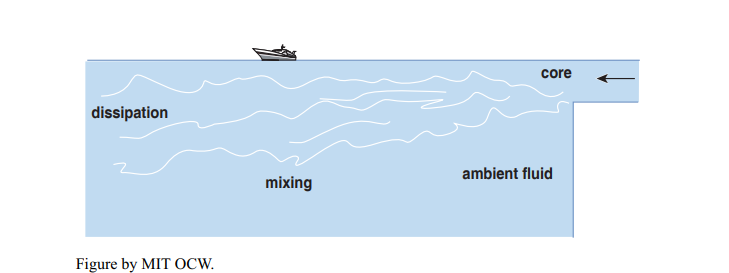
You’re probably thinking: What does all of this hydrodynamics have to do with deltas? To make the connection more direct, think in terms of a jet with ambient fluid ambient fluid core mixing mixing dissipation a somewhat different geometry: a free-surface channel flow entering a body of still water, as might a river flowing into a lake (Figure 8-36). The essential nature of the jet is no different; what is different is the geometry. The jet still mixes with the ambient fluid, but it can’t mix upward, only sideways and downward. If the channel flow is muddy water, you can imagine how the jet would appear from the air: a spreading mass of muddy water, surrounded by clear water, with a core of muddiest water extending outward from the entrance and the muddiness gradually decreasing outward in all directions.

Figure 8-36, except that the shape of the jet is not axially symmetric.)

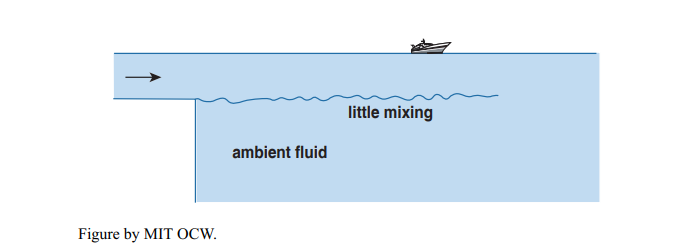
Now I’ll throw in another complicating factor. The jet described in the preceding paragraph is a good model of a river entering a fresh-water lake or reservoir. But, as we all know, the ocean is salty, and, because it’s salty its density is significantly greater, by an important few percent, than that of fresh water. That impedes vertical mixing of the jet with its surroundings, while not affecting its horizontal mixing greatly. The reason is that the density stratification that develops between the overlying fresh-water jet and the underlying salt-water medium is gravitationally stable, and it takes work to disrupt or break down that stratification by mixing. The jet may be able to do some vertical mixing, but the extent is much reduced. The jet ends up being largely in the form of a kind of horizontally oriented fan, spreading laterally but not downward (Figure 8-37).

Sediment Deposition in Deltas

Now that you have a good mental picture of the hydrodynamics of the delta environment, think about sediment deposition in the delta environment. Think in terms of the jet shown in Figure 8-36 or Figure 8-37, with the reservation that the depth of water in the water body is not infinitely deep—perhaps only several times the depth of flow in the approach channel (that is, the stream or river).

Figure 8-37: except that the shape of the jet is not axially symmetric.)

Suppose that the stream is carrying both bed load and suspended load. You know what’s going to happen: the bed load tends to be dropped out rapidly, at and near the entrance of the jet, because the sediment particles have relatively large settling velocities, but the finer part of the load is carried for greater distances away from the entrance, participating in the lateral mixing while it settles slowly to the bottom of the water body.

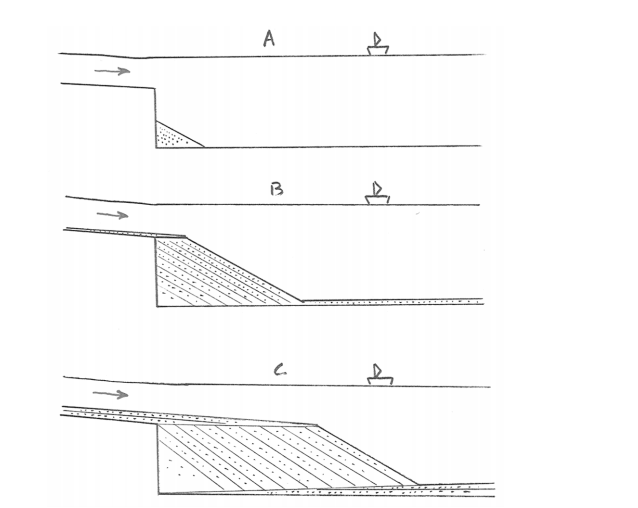
Think now specifically about the deposition of the bed load. At first, of course, it just makes a pile of sediment at base of the water body below the jet entrance. Eventually the pile builds up to reach the jet entrance. From then on, as the sediment comes to rest as the jet emerges into the water body, a wedge of coarse sediment builds forward into the water body, as sediment is deposited at the brink of a sediment body and slides down an angle-of-repose slope. Figure 8-38 shows three stages in the process, and Figure 8-39 shows a plan view.

Note, in particular, from Figure 8-38 that in the later stages the delta body consists of three rather distinct parts: topsets, foresets, and bottomsets. The foresets we just dealt with. The bottomsets are readily understandable as well: as the foresets build forward, they bury earlier-deposited finer sediment, which fell from suspension at some distance from the jet entrance.

The topsets require a bit of further explanation. Keep in mind that the river flowing into the water body has some nonzero slope. (That’s what keeps the water flowing, remember.) I purposely showed that slope in Figure 8-38. The outbuilding of the foresets has the effect of shifting the point of entrance of the jet in the direction out into the water body. That causes the downstream-most part of the river profile to rise at all points. That happens by sediment deposition. More specifically, a very small part of the passing bed load is extracted from the flow to come to permanent rest on the river bed, thereby building the profile of the river upward. These are the topsets of the delta

Figure 8-38. Building of a delta as a river enters a body of standing water. A) The earliest stage. B) A somewhat later stage. C) An even later stage, showing topsets, foresets, and bottomsets.

Finally, Figure 8-39 shows a plan view of the delta in Figure 8-38 after the delta has built out into the water body for an appreciable distance. The margin of the delta forms an arc, because sediment builds not just forward but also with a lateral component. Why? Basically because the tendency for deposition along the axis of the flow leads to a slight axial ridge, and then the flow tends to flow laterally off that ridge, down the slight sideways slopes of the delta body.

Figure 8-38. T, topsets; F, foresets; B, bottomsets.

Large Deltas in Nature

The delta described in the preceding section, and shown in Figures 8-38 and 8-39, is representative of the way deltas develop when a relatively small stream or river enters a water body in which currents and waves are minor. Such deltas are called Gilbert deltas, in honor of an early geomorphologist, G.K. Gilbert, who made the first systematic studies of such small deltas in the western U.S. in the late 1800s.

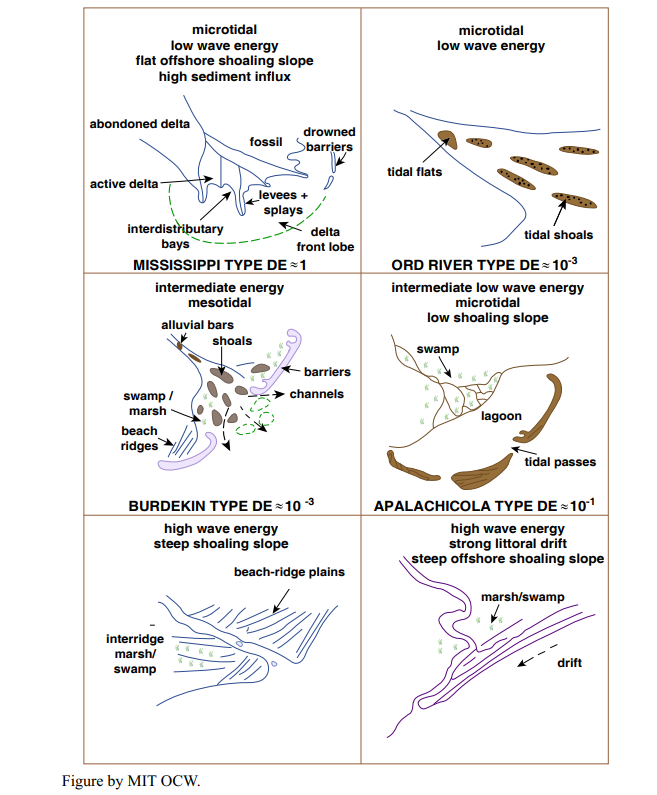
At this point we need to address the various complicating factors that set in when the delta-building river is larger and the water body into which the delta is building is not as placid as was assumed in the preceding section. Figure 8-40 shows one of several classifications of deltas.

Let’s deal first with the behavior of the river. The topset surface, which we’ll call the delta plain, is not a smooth surface. One reason for its nonsmoothness, even if only sand and gravel bed load is being carried by the river, is that the delta plain is braided. (Go back to the chapter on rivers to review the nature of braiding in streams and rivers.)

Figure 8-40. Classification of deltas. (From Carter, 1988.)

A more important reason, applicable to large mixed-load rivers, is that there is a strong tendency for upbuilding of the flow-carrying channel, deposition of natural levees, and occasional avulsion to relocate the channel to slightly lower areas on the aggrading delta plain. Typically there are two or more active channels, carrying water and sediment, operating on the delta plain at the same time. All the time, these shift around, avulse, and become abandoned, and new ones form. In that way, over time all of the delta plain is built up uniformly but with very complex internal structure in detail. The individual flow-carrying channels are called distributary channels. The next time you look at a map of Louisiana, note how the most recent active area of the Mississippi delta is building out into the Gulf of Mexico in the form of a hand-like body with several active distributaries (locally called “passes”).

Now we have to contend with the various effects that the water body itself has on the growing delta. We need to be concerned particularly with the action of waves, tides, and currents. Each of these factors is able to mold the morphology of the delta, in complex ways.

currents: The effects of throughgoing coast-parallel ocean currents are the easiest to understand. They tend to sweep the delivered sediment in one direction, causing slight to extreme asymmetry of the delta. Currents offshore of the mouth of the Amazon are so strong that even given the enormous sediment load of the river the delta does not protrude greatly into the ocean, the way the Mississippi delta does.

waves: ocean waves, approaching at a large angle to the coastline, tend to blunt the margin of the delta, giving it a fairly regular, arcuate shape. The Nile delta is the classic example.

tides: In regions with a large tidal range and strong tidal currents, deltas are shaped by strong back-and-forth flow in the various distributary channels, making for a strongly dissected delta body. The classic example is the Rhine delta, in the Netherlands.

The Mississippi delta is an excellent example of a delta that is dominated by the river itself rather than the water movements in the water body. That’s why the delta is able to build outward in long salients. Such a delta is picturesquely called a bird’s-foot delta. (Look again at a map of the Mississippi delta to get the concept.)