3.1: Orbital Mechanics
- Page ID
- 3519
Orbital mechanics is a branch of planetary physics that uses observations and theories to examine the Earth's elliptical orbit, its tilt, and how it spins. Observations of the orbital behavior of planets, moons or satellites (orbiters) can provide information about the planet being orbited through an understanding of how these orbital properties are related to gravitational forces.
Humans have been studying orbital mechanics since 1543, when Copernicus discovered that planets, including the Earth, orbit the sun, and that planets with a larger orbital radius around their star have a longer period and thus a slower velocity. While these may seem straightforward to us today, at the time these were radical ideas. Johannes Kepler elaborated on Copernicus' ideas in the early 1600's, stating that orbits follow elliptical paths, and that orbits sweep out equal area in equal time (Figure \(\PageIndex{1}\)). The same (blue) area is swept out in a fixed time period. The green arrow is velocity. The purple arrow directed towards the Sun is the acceleration. The other two purple arrows are acceleration components parallel (tangent to the orbit) and perpendicular to the velocity.

Following on this observations Kepler also observed the orbital periods and orbital radius for several planets. For each planet he considered various relationships between these two parameters to determine how they were related. He determined that there is a constant relationship for all the planets orbiting the sun
\[T^2\propto R^3\]
That is, for each planet orbiting another (much larger) object (the Sun), the square of the orbital period is proportional to the cube of the orbital radius. In addition, he found that the constant of proportionality was the same for all the planets orbiting the sun. This relationship is true for any set of smaller objects (planets) orbiting a (much) larger object, which is why this is now known as Kepler's Third Law:
\[ \frac{T^2}{R^3} = Constant \]
Below we will see that this constant is related to Newton's Law of Universal Gravitation, and therefore can also give us information about the mass of the object being orbited. But first, let's see how one can use Kepler's third law to for two applications.
Orbital Period or Radius of a Satellite or other Object
Consider two planets (1 and 2) orbiting the sun. If the proportionality above it true for each planet, then we can set the fractions equal to each other, and rearrange to find,
\[\frac{T_1^2}{T_2^2}=\frac{R_1^3}{R_2^3}\]
Why would we do this? Well, suppose we want to launch a satellite into outer space that will orbit the Earth at a specified orbital radius, \(R_s\). For example, the best height for taking Google Earth imagery is about 6 times the Earth's radius, \(R_e\). We can use Kepler's Third Law to determine the orbital period, \(T_s\) of the satellite.
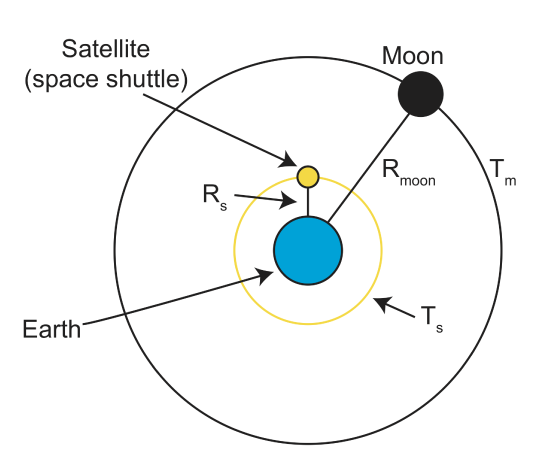
We are know the orbital period of the moon is \(T_m = 27.3217\) days and the orbital radius of the moon is \(R_m = 60\times R_e\) where \(R_e\) is the radius of the Earth. Substituting
\[\begin{align*} \left(\frac{T_s}{T_m}\right)^2 &=\left(\frac{R_s}{R_m}\right)^3 \\[4pt] T_s^2 &=T_m^2\left(\frac{R_s}{R_m}\right)^3 \\[4pt] T_s &=T_m\left(\frac{R_s}{R_m}\right)^{\frac{3}{2}} \\[4pt] &=27.3217\left(\frac{6 R_e}{60 R_e}\right)^{\frac{3}{2}} \\[4pt] &=27.3217\left(\frac{1 }{10 }\right)^{\frac{3}{2}} \\[4pt] &=27.3217\left(0.0317\right) \\[4pt] &= 0.86\;days \end{align*}\]
So, the orbital period is about 1 day (with more precise numbers, you will find it is exactly one day... a geosynchonous orbit). You could also start with Ts and determine the orbital radius. A note about units: you should use what units make sense as long as they are consistent, ie., they are the same for both of the orbital periods and both orbital radii, so they cancel out.
Many geological and geophysical observations are made with orbiting satellites, including missions that measure Earth's gravity field, topography, changes in topography related to earthquakes and volcanoes (and other things), and the magnetic field. Other satellites monitor ice mass, vegetation, and all sorts of chemical signatures in the atmosphere. Planetary scientists also send orbiters to other planets to make similar measurements (okay not vegetation).
Kepler's Third Law can also be used to study distant solar systems. Using a telescope, one can detect other planets around stars by observing a drop in the brightness of the star as the planet transits between the star and the telescope. By observing the time between transits, we know the orbital period. Kepler's Third law can be used to determine the orbital radius of the planet if the mass of the orbiting star is known (\(R^3 = T^2 - M_{star}/M_{sun} \), the radius is in AU and the period is in earth years).
The Fastest Path from one Planet to Another
Kepler's 3rd law can also be used to determine the fast path (orbit) from one planet to another. This fastest path is called a Hohmann transfer orbit, named for the german scientist Walter Hohmann who first published the orbit in 1952 (see more in this article). In the above discussion of Kepler's Law we referred to \(R\) as the orbital radius. In fact, because almost no planet, satellite, or moon is actually on a perfectly circular orbit \(R\) is the semi-major axis of the elliptical path of the orbiting object. For the Hohmann Transfer orbit, we need to be more explicit about treating the orbits as elliptical.
Take for example Mars orbiting the Sun. The Sun is not located at the center of the ellipse, but slightly to one side (at one of the two foci of the ellipse). Mars is closest to the Sun at Perihelion and farthest away at Aphelion.
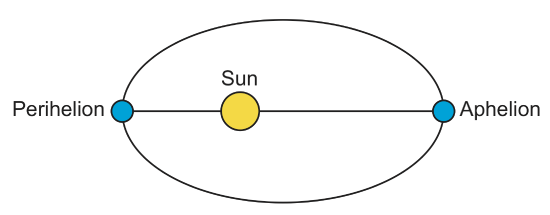
Now, let's consider the fastest path from Earth to Mars using Kepler's Third Law.
Hohmann Transfer Orbits
A transfer orbit is an intermediate elliptical orbit that is used to move a satellite or other object from one circular, or largely circular, orbit to another. Using Figure \(\PageIndex{3}\), we will calculate how long it would take to reach Mars in the most efficient orbit. Note from the figure, that the when Earth is at Perihelion and Mars is a Aphelion, the path connecting the two planets is an ellipse. This path is the Hohmann Transfer Orbit and is the shortest (in time) path between the two planets. Note that when the satellite leaves the Earth, Mars will not yet be at Perihelion, so the timing is important. The other important thing to note, is that it is not very often that the orbits line up exactly such that a Hohmann transfer orbit is possible. However, knowing that it is the fastest path places clear limits on missions to Mars (and similarly missions to other planets) including sending manned missions.

Solution
We know that the path is an elliptical orbit around the sun, and it grazes the orbit of Mars at aphelion.
For Hohmann Transfer orbit, the semi-major axis of the elliptical orbit is \(R_n\) and is the average of the Earth's distance from the sun (at Perihelion), \(R_e\) and the distance of Mars from the sun (at Aphelion), \(R_m\),
\[\begin{align*} R_n &=\frac{1}{2}(R_e+R_m) \\[4pt] &=\frac{1}{2}(1+1.524) \\[4pt] &=1.262\, AU \end{align*}\]
Next, noting that both the Earth and the object traveling on the Hohmann Transfer Orbit are both orbiting the sun, we use this Kepler's Law to determine the period of the object on the Hohmann Transfer orbit,
\[\left(\frac{T_n}{T_e}\right)^2 = \left(\frac{R_n}{R_e}\right)^3 \nonumber\]
\(R_e= 1 \) AU and \(T_e=1\) earth-year
\[ \begin{align*} (T_n)^2 &= (R_n)^3 \\[4pt] (T_n)^2 &= (1.262)^3 \\[4pt] (T_n)^2 &= 2.0099 \\[4pt] T_n &=1.412\;years \end{align*}\]
This is the full orbit time, but a a transfer takes only a half orbit (1.412/2 = 0.7088 year).
Therefore the shortest orbital path to Mars from Earth takes about 8 months.
Both the examples above illustrate the way that Kepler's Third Law can be used determine orbital information about planets, moons or satellites. The next step is to connect Kepler's 3rd law to the object being orbited. That it, we want to know the constant of proportionality between the \(T^2\) and \(R^3\). What is the physical meaning of this constant and what does it depend on?
Determining the Mass of a Planet
In the late 1600s, Newton laid the groundwork for this idea with his three laws of motion and the law of universal gravitation. As you were likely told in elementary school, legend states that while attempting to escape an outbreak of the bubonic plague, Newton retreated to the countryside, sat in an orchard, and was hit on the head with an apple. This lead him to develop his ideas on gravity, and equate that when an apple falls or planets orbit, the same physics apply.
Newton's Law of Gravity
Newton, building on other people's observations, showed that the force between two objects is proportional to the product of their masses and decreases with the square of the distance:
\[F=\frac{GMm}{r^2} \nonumber\]
where \(G=6.67 \times 10^{-11}\) m\(^3\)kg s\(^2\) is the gravitational constant.
This gravitational force acts along a line extending from the center of one mass to the center of the second mass.
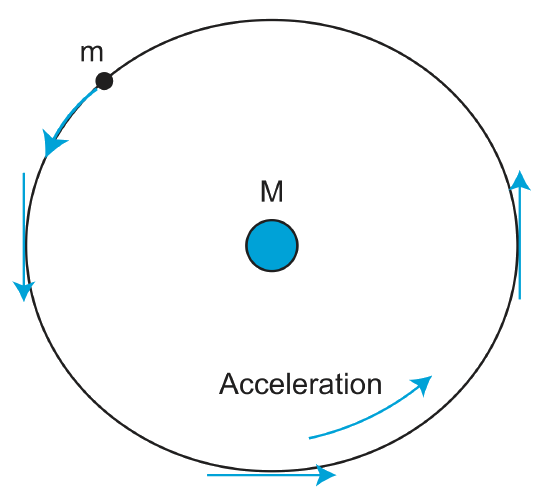
For an object orbiting another object, Newton also observed that the orbiting object must be experiencing an acceleration because the velocity of the object is constantly changing (change direction, not speed, but this is still an acceleration). Newton's second Law states that without such an acceleration the object would simple continue in a straight line. Since the object is experiencing an acceleration, then there must also be a force on the object. This is force is called the Centripetal force and is proportional to the velocity of the orbiting object, but decreases proportional to the distance.
\[ F=\frac{mv^2}{r} \nonumber\]
The last step is to recognize that the acceleration of the orbiting object is due to gravity. Therefore we can set these two forces equal,
\[ \frac{GMm}{r^2} =\frac{mv^2}{r} \nonumber\]
Or, solving for the velocity of the orbiting object,
\[ v^2 =\frac{GM}{r} \nonumber\]
Next, the velocity of the orbiting object can be related to its radius and period, by recognizing that the distance = velocity x time, where the distance is the length of the circular path and time is the period of the orbit, so
\[v=\frac{d}{t}=\frac{2\pi r}{T} \nonumber\]
where 2\(\pi\)r is the circumference and \(T\) is the orbital period.
Substituting for v, we find
\[ \left(\frac{2\pi r}{T}\right)^2 =\frac{GM}{r} \]
\[\frac{4\pi^2r^2}{T^2} =\frac{GM}{r}\]
And finally we solve for \(T^2\),
\[ T^2 =\frac{4\pi^2}{GM}r^3\nonumber \]
We can rearrange this equation to find the constant of proportionality constant for Kepler's Third law,
\[ \frac{T^2}{r^3} =\frac{4\pi^2}{GM} \label{eq10} \]
The constant of proportionality depends on the mass, \(M\) of the object being orbited and the gravitational constant, \(G\).
Using \ref{eq10}, we can determine the constant of proportionality for objects orbiting our sun as a check of Kepler's third Law.
Planets Orbiting Sun
The mass of the sun is
\( M = M_{sun} = 1.9891\times10^{30} \) kg
We rewrite Kepler's 3rd Law as
\[T^2=K R^3\]
where \(K\) is a constant of proportionality. Now, we calculate \(K\),
\[ \begin{align*} K&=\frac{4\pi^2}{GM} \\[4pt] &=2.97 \times 10^{-19}\frac{s^2}{m^3} \end{align*}\]
For any object orbiting the sun, \(T^2/R^3 = 2.97 \times 10^{-19} \)
Also note, that if \(R\) is in AU (astonomical units, 1 AU=1.49x1011 m) and \(T\) is in earth-years, then
\[K=0.9916 \approx 1 \nonumber\]
Now knowing this proportionality constant is related to the mass of the object being orbited, gives us the means to determine the mass this object by observing the orbiting objects. Solving equation \ref{eq10} for mass, we find
\[M=\frac{4\pi^2}{G}\frac{R^3}{T^2} \label{eq20}\]
By observing the orbital period and orbital radius of small objects orbiting larger objects, we can determine the mass of the larger objects.
This is the how planetary scientists determined the mass of Earth, the mass of other planets in our solar system that have moons, the mass of the moon using an orbiter, and the mass of other stars when orbiting planets can be observed.
Knowing the mass of a planet is the most fundamental geophysical observation of that planet, and with other observations it can be used to determine the whether another planet has a core, and relative size of the core and mantle. With this information, model of the planets can be made to determine if they might be convecting like Earth, and if they might have plate tectonics.
Mass of the Earth
What is the mass of the Earth, \(M_e\)?
Solution
This is a direct application of Equation \ref{eq20}.
\[M_e=\frac{4\pi^2}{G} \left(\frac{R_{moon}^3}{T_{moon}^2}\right) \nonumber\]
with \(R_{moon}=384 \times 10^6\, m \) and \(T_{moon}=27.3\, days=2358720\, sec\).
\[M_e=6.02 \times 10^{24}kg\]
This is quite close to the accepted value for the mass of the Earth, which is \(5.98 \times 10^{24} kg\).
See the NASA Planetary Fact Sheet, for fundamental planetary data for all the planets, and some moons in our solar system.


