1.4: Failure of Rocks
- Page ID
- 3537
At shallow depths, rocks record permanent deformation caused by either fracture of the rock or frictional sliding on existing fractures. This failure often occurs dramatically in the form of earthquakes occurring with displacement across the fault of centimeters to tens of meters. In most cases both fracture and frictional sliding occur through shear deformation (shear strain) along a discrete surface. Both fracture and friction are described by experimentally-determined relationships, which relate the shear resistance to the applied normal stress \(\sigma_n\) and failure properties of the rock. These relationship define the state of stress on the failure plane at the point of failure.
Tectonic Stress and Stress Components on Faults
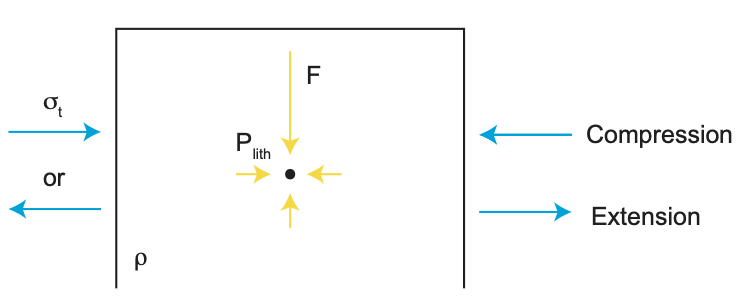
Tectonic stresses in the crust arise due to density anomalies in the mantle, which drive convection and move the plates. However, if we are concerned with the stresses acting on faults in the crust, we can ignore the details of where these stresses come from and instead treat the tectonic stress as a horizontal normal stresses. In this case, tectonic stresses either act in compression (a positive normal stress) or in extension (a negative normal stress).
To consider the total stress-state in the crust, we start from an assumption that the state of stress is equal to the lithostatic pressure and add the tectonic stress to get the stress component in the horizontal direction:
\[ \sigma_{H} = P_{lith} + \sigma_{t} \]
Except in cases of very shallow rock (less than about 500 m), all the components of stress in the rock are positive due to the increase in the lithostatic pressure with depth. This means that the magnitudes of tectonic stresses are smaller than the magnitude of the lithostatic stress at depths greater than about 500 m.
Andersonian Theory of Faulting
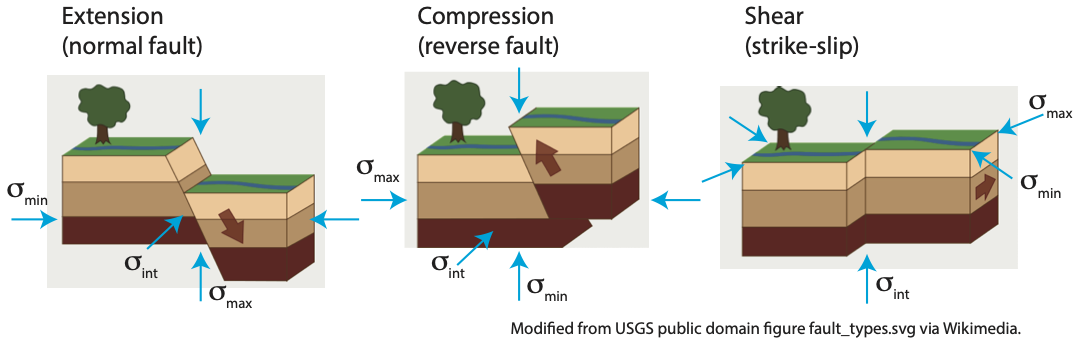
While the magnitude of the horizontal stress is positive, it is the difference in stress magnitude between two orthogonal directions that determine whether a region experiences compression (with reverse faults), extension (with normal faults) or shear (strike-slip faults). Figure \(\PageIndex{4}\) shows the three different kinds of faults arising from three different stress-states. The stress state is described by the maximum, intermediate and minimum magnitude principal stresses, \(\sigma_{max} \ge \sigma_{int} \ge \sigma_{min}\). Remember the three principal stress are always orthogonal to each other.These are also referred by as \(\sigma_{1} \ge \sigma_{2} \ge \sigma_{3}\) (note these only have one number in the subscript, so these refer to the principal stresses). Extension, characterized by normal faulting, occurs where \(\sigma_{max}\) is vertical and extension occurs parallel to the \(\sigma_{min}\) direction. For this case think of squeezing playdoh between your fingers, it will extend outward in the direction of least resistance. Shortening, characterized by reverse faulting, occurs where \(\sigma_{max}\) is horizontal and \(\sigma_{min}\) is vertical. In this case, shortening occurs parallel to the \(\sigma_{max}\) direction. Finally, horizontal shearing characterized by strike-slip faulting, occurs where \(\sigma_{max}\) and \(\sigma_{min}\) are both horizontal. The orientation of the strike-slip fault will be at an angle to both \(\sigma_{max}\) and \(\sigma_{min}\). The exact angle depends on the value of the friction on the fault, but is usually in the range of 30 - \(60^\circ\). This first order description of the relationship between stresses and fault orientation is called the Andersonian Theory of Faulting.
Stress Components in the Principal Stress Directions
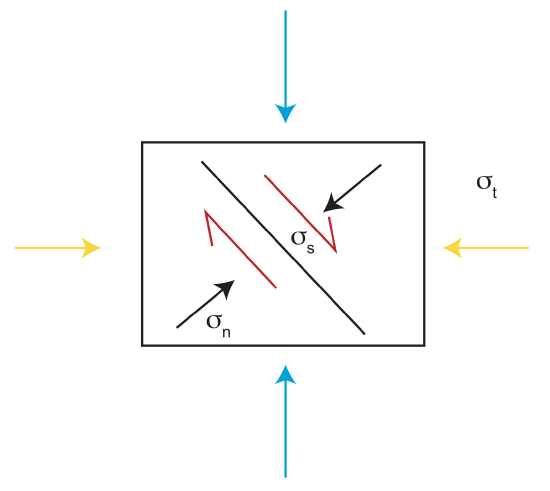
Existing faults and fractures can have any orientation in the crust, and almost all of these orientation will result in both shear stress and normal stress acting on the fault plane. However, there are 3 (and only 3) possible fault/fracture plane orientations that will have a zero shear \(\sigma_{s}=0\). These three planes are the planes that are perpendicular to the principal stress directions (Figure \(\PageIndex{6}\)). This is why the principal directions are normal stresses, and this is why we only need to know these three principal stresses to fully describe the state of stress. Near the surface of the Earth, it is likely that one of the principal stress directions aligns with the vertical, but the two horizontal principal stress can be in any orientation. When looking at the figure below, imagine taking one of the planes and rotating it slightly. The stress component (vector) acting on that plane can now expressed in terms of component parallel to the fault plane and a component perpendicular to the fault plane. All other planes have both shear and normal stresses acting across the plane.
Example: Stress-State on the San Andreas Fault
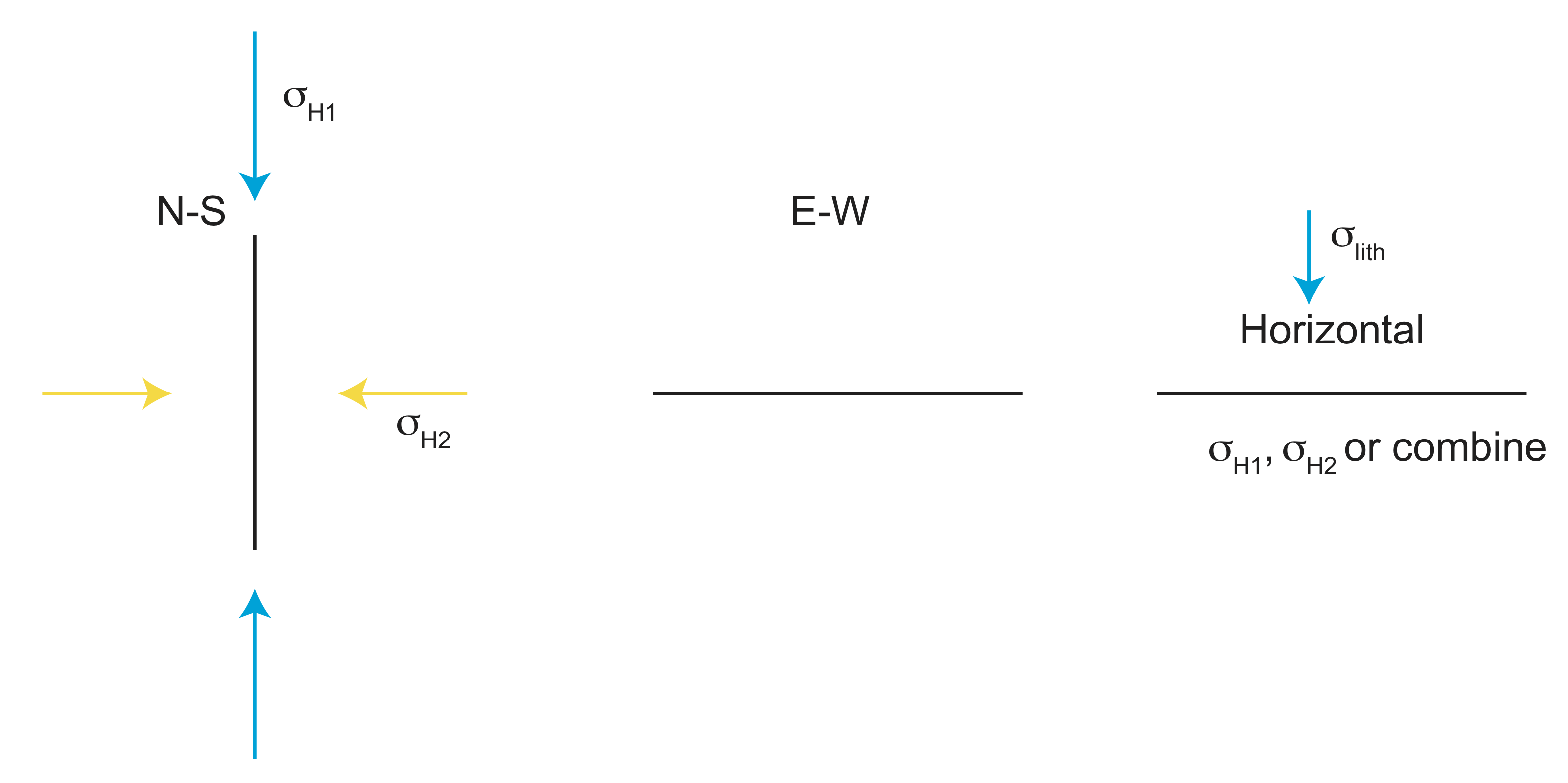
The San Andreas Fault is a large strike-slip fault the runs most of the length of California. It is the plate boundary between the Pacific Plate to the west and the North American plate to the East. This fault has been active for about 30 million years. During that time the shape of the fault (or its orientation) have changed as the stress state along the plate boundary has changed. Figure \(\PageIndex{5}\) is a schematic map view of a section of the fault showing the orientation of the fault relative to the maximum stress, \(\sigma_{H1}\) and the minimum stress \(\sigma_{H2}\). Note that in this case, both horizontal components of the lithostatic stress are modified by a tectonic stress: a roughly north-south oriented positive tectonic stress, \(\sigma_{t+}\), and a roughly east-west oriented negative tectonic stress, \(\sigma_{t+}\). This state of stress and also be expressed in terms of the stress acting perpendicular and parallel to the fault surface (Figure \(\PageIndex{5}\)B). The magnitude of these stresses depend on the exact orientation of the fault relative to the normal stresses. In order for the motion to occur along the fault, the shear stress \(\sigma_s\) must be larger than the frictional resistance to sliding between the two blocks.


Fracture
Fracture of a rock is described by the Mohr-Coulomb Fracture Criteria. This is an empirical relationship, which states that failure by fracture occurs when the shear stress acting on the rock exceeds the shear fracture strength given by
\[\sigma_{s-frac} = tan(\phi) \sigma_{n} + c\]
where \(\phi\) is the angle of internal friction, and \(c\) is the cohesion. The term \(tan(\phi)\) can be thought of as an internal friction. The angle of internal friction for rock has a typical values \(30^\circ\), but ranges from \(20-45^\circ\). The cohesion term sets the minimum values of the shear fracture strength, which occurs when the normal stress is zero. Cohesion for rock is typically about 0.1 MPa for silts or clays, but 10 MPa for other rocks. As we will see below, the failure criterion for frictional sliding is defined by a similar equation, with similar magnitudes for the parameters. Therefore, it is not necessary to know if an earthquake occurred on an existing plane or formed a new fracture: the analysis of the stresses or prediction of failure planes will be very similar in both cases.
The plot below shows the Mohr-Coulomb criterion (blue) and Byerlee's law (green; see next topic). These two failure laws predict similar levels of shear stress resistance to failure at a given normal stress acting across the plane. The shear stress resulting from tectonic forces needs to be larger than the shear stress resistance in order for failure to occur.
Frictional sliding
Failure by frictional sliding is described by Byerlee's law, an empirically-derived equation based on laboratory experiments originally carried out James Byerlee in the 1960's and 70's. The general form of Byerlee's law is given by
\[ \tau = \mu_s \sigma_n + C \]
where \(tau\) is the stress stress resisting sliding along the fault, \(\mu_s\) is the coefficient of friction and \(C\) is the cohesion across the fault surface. This equation gives the shear stress needed to cause sliding across the fault. That is, when the tectonically derived shear stress acting on the plane is higher than \(\tau\) then sliding will occur.
Byerlee showed that the coefficient of friction for most rocks is remarkably uniform, but it does vary systematically depending on the magnitude of the normal stress:
\[ \begin{align*} \tau &= 0.85\sigma_{n} & \textrm{when}\, \sigma_n < 200\, \textrm{MPa} \\[4pt] \tau &= 50 + 0.6\sigma_{n} & \textrm{when}\, 200<\sigma_n < 1700\, \textrm{MPa} \end{align*}\]
where, \(\sigma_n\) and \(\tau\) are in units of MPa. Note that when \(\sigma_n > 200\) MPa, there is a cohesion term of 60 MPa. These equations capture the fact that there is no cohesion at low normal stress, while at higher normal stress there is a threshold shear stress that must be overcome before any sliding occurs. This maybe a familiar phenomena to anyone who has tried to slide furniture across a tile or wood floor. A light chair (low normal stress) moves immediately when we start pushing or pulling it across the floor, whereas as heavy desk or couch seems to resist moving until sufficient force is applied, buy then it readily slides as long as we maintain that same threshold force.
Recall that normal stress in the crust is primarily determined by the lithostatic stress, so the normal stress will increase with depth even if there is no tectonic stress. Tectonic stresses are needed to create a shear stress acting on the fault that exceeds the shear stress resisting sliding. That is, sliding occurs when
\[\tau_{tect} > \tau\]
While the values for \(\mu_s\) given by Byerlee's law are appropriate for many rocks, certain clays, talc and serpentinite have coefficient of friction of 0.1-0.2. Clays and talc are often found on exhumed fault zones and in drill cores across active faults. Therefore, the frictional properties on faults themselves may not directly reflect the properties of intact rock surrounding the faults.
Why do the failure criterion for fracture and frictional sliding have the same form and similar values? This is likely because at a microscopic scale fracture occurs through opening of tiny fracture, and frictional sliding on these tiny fracture. The tiny fractures then link up to cause a through-going fracture.
What determines the maximum depth of earthquakes in the crust? Note that shear stress for required to cause fracture or frictional sliding increases with increasing normal stress. Because the normal stress (pressure) increases with depth in the crust, a larger tectonically-derived shear stress is required to cause failure at greater depths. This is why faulting is typically limited to depths of less than about 15 to 30 km except in regions that are very cold (or when other processes can act to reduce the normal stress).
Will the fault fail?
Below is a sketch of a portion of a fault at a depth of 10 km. Both lithostatic stress and tectonic stress are acting on this point to determine the state of stress on the fault. It is been independently determined given the orientation of the fault, the normal stress acting on the fault is \(\sigma_{n}\)=300 MPa, and the shear stress acting on the fault is \(\tau_{tect} = 120\) MPa. Use Byerlee's law to determine if the fault should fail.
Because \(\sigma_n> 200\) MPa, we use the second part of Byerlee's law:
\[ \begin{align*} \tau &= 50 + 0.6 (300) \\[4pt] &= 50 + 180 \\[4pt] &=230\, \textrm{MPa} \end{align*}\]
Since \(\tau_{tect} < \tau\) the fault will not fail: the shear stress resisting sliding (230 MPa) is larger than the shear stress acting along the fault (120 MPa).


