1.3: Elastic Deformation
- Page ID
- 3534
What Type of Deformation is Recorded in Rocks?
The deformation recorded in the rock record provides a direct measurement of the total strain that the rock has undergone. However, it is important to note two things. First, knowing the total strain does not give us information about the strain path. For example, I can stretch and compress a spring many times and then stop. I can then measure the final strain, but that measurement does not tell me how much I stretched and compressed the rock beforehand. In other words, we know the final strain, but not the history of how that final strain was achieved.
Second, rocks record permanent deformation. Again thinking about the spring. I can stretch and compress the spring many times, but it always returns to its original shape. There is no permanent deformation so there is no record of the deformation. However, if I pull on the spring very hard I can cause it to stay partly stretched even when I let go. This is permanent deformation, which is also referred to as irrecoverable strain. In the case of the spring it occurs when the force applied is large enough that it causes the spring to deform plastically (this is a type of failure typical of metals). The same is true for rocks, low stress in a rock causes elastic deformation that is not permanent. This is referred to as recoverable strain. This elastic deformation is not recorded in the rock record. The deformation recorded in the rocks occurs when the rocks break (fail) or flows viscously (a type of crystal-scale failure) or plastically (also a crystal-scale failure process).
Elastic deformation is the dominant form of deformation at shallow depths in the crust and lithosphere because both the temperature and pressure are low. However the crust and lithosphere are also brittle and when the stress is big enough, failure by fracture or frictional sliding also occurs. Viscous and plastic deformation typically occur deeper and at higher pressures and temperatures than elastic deformation. In between the shallow elastic region and deeper viscous region there is a region that deforms through both mechanisms (both mechanisms accommodate roughly equal amounts of deformation). This region is referred to as the brittle-ductile transition and rocks here include cataclasites (features of viscous flow with pervasive micro-cracks), mylonites and pdeudotachylites (melting).
Even though elastic deformation is not preserved in the rock record, the elastic strength of the rock still supports the stress in the rock up until failure, so we need to be able to quantify the elastic behavior. For example, slow steady motion of tectonic plates causes elastic deformation in the region surrounding a fault. In between earthquakes this elastic deformation builds up until the stress inside the rock exceeds the friction on the fault. So, even though the elastic deformation is released in the surrounding rock, the history of this process is recorded by the earthquake. Similarly, in a laboratory experiment or when computer simulations are used to model the deformation of the crust or lithosphere, we can apply forces that result in a stress in the rock and we can observe or calculate the resulting strain. We will not go into a full description of how this is done, but we will touch on a few key aspects that help a geologist think about the state of stress in the crust or lithosphere.
Elastic Deformation
While the spring is an appropriate model for linear strain, in order to consider the three-dimensional deformation of rocks, we need to consider a block of material or a volume of rock. For the spring the elastic response is determined by a single parameter, the spring constant (or the elasticity of the spring). For the volume of rock we need (at least) two parameters: the Young's modulus and Poisson's ratio.
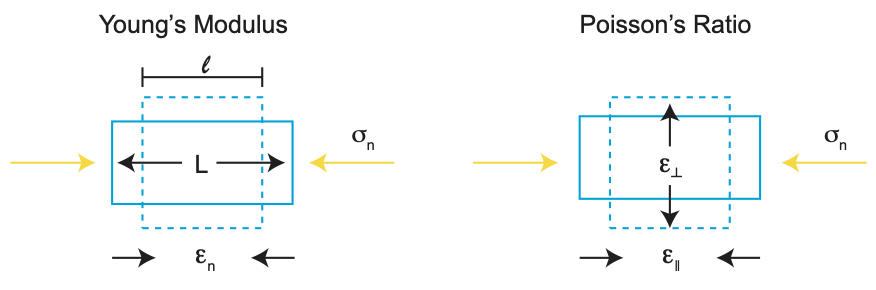
Young's Modulus
Young's modulus, \(E\), quantifies the relationship between an applied linear stress \(\sigma_n\) and the resulting linear strain \(\epsilon_n\) when no other stresses act on the material:
\[E=\frac{\sigma_n}{\epsilon_n}\]
Since stress has units of Pascals and strain is dimensionless, Young's modulus has the same units as stress (Pa). The Young's modulus quantifies the ability of an object to resist deformation through the elastic strength arising from the crystal structure of the rock. Typical values for Young's modulus are in the range of 10 MPa to 70 GPa (see Table \PageIndex{1}\)
For Earth materials, Young's modulus is measured in the laboratory by taking small cylinders of rock, compressing them in a vice-like apparatus with a known force, and then measuring the change in length. The stress and strain are determined (knowing the area of the top and bottom of the cylinder and its length) and then Young's modulus is calculated. Note that when this experiment is done there is no stress acting on the curved sides of the cylinder, only on the top and bottom. This state of stress is referred to as a uniaxial stress-state. However, note that even though there is no stress on the sides of the cylinder, there is a strain perpendicular to the sides because the compression of the cylinder in one direction causes it to bulge out in the perpendicular directions. The amount that the material bulges out is determined by the second elastic property, the Poisson's ratio.
| Rock Type | Young's Modulus | Rock Type | Young's Modulus |
|---|---|---|---|
| Soils | 10 - 200 MPa | Granite | 10 - 70 GPa |
| Sand | 10 - 70 MPa | Limestone | 15 - 55 GPa |
| Sandstone | 1 - 20 GPa | Steel | 200 GPa |
| Shale | 1 - 70 GPa | Glass | 45 GPa |
Poisson's ratio
Poisson's ratio, \(\nu\), quantifies the amount that a material deforms in one direction relative to the amount it deforms in the perpendicular direction:
\[\nu=\frac{-\varepsilon_{\perp}}{\varepsilon_{\parallel}}\]
where \(\varepsilon_{\perp}\) is referred to as lateral strain and \(\varepsilon_{\parallel}\) is referred to as the longitudinal strain. (Both lateral and longitudinal strain are normal strains.) Note that there is a minus sign in the equation for Poisson's ratio because either the lateral or longitudinal strain will be negative (depending on whether the applied force causes stretching or shortening). The range of expected values for Poisson's ratio for Earth materials is 0 to 0.5, with typical values of 0.15-0.35. A value of 0.5 corresponds to a perfectly incompressible material (there is not internal compression, so the strain in two perpendicular directions exactly compensates for the applied strain). Water has a Poisson's ratio of 0.5. Poisson's ratio can also be negative (down to -1): these special synthetic materials are called anti-rubber or auxetics, which expand outward as they are stretched. Currently, there are no naturally occurring Earth materials with a negative Poisson's ratio.
| Rock Type | Poisson's ratio | Rock Type | Poisson's Ratio |
|---|---|---|---|
| Sandy soil | 0.25 - 0.40 | Granite | 0.1 - 0.3 |
| Sandstone | 0.21 - 0.38 | Limestone | 0.18 - 0.33 |
| Shale | 0.2 - 0.4 | Steel | 0.3 |
Elastic Deformation in 3D
The elastic response of an applied stress in 2D can be extended to 3D. Here, for simplicity, we will only consider the normal (linear) components of strain and stress (Similar equations exist for the shear components). Consider the normal strain in one direction resulting from normal stresses applied in three orthogonal directions. As noted above, for an elastic solid, a stress applied in one direction will also cause a strain in the perpendicular directions. Therefore, the linear strain in the x directions depends on the strain caused by the stress in the x direction, but it also depends on the strain caused by the stresses acting in the y and z directions. Therefore, the components of normal strain in an elastic solid, acting in three orthogonal directions are given by:
\[\varepsilon_{xx}=\left(\frac{1}{E}\right)(\sigma_{xx}-\nu(\sigma_{yy}+\sigma_{zz}))\]
for the x direction,
\[\varepsilon_{yy}=\left(\frac{1}{E}\right)(\sigma_{yy}-\nu(\sigma_{zz}+\sigma_{xx}))\]
for the y direction, and
\[\varepsilon_{zz}=\left(\frac{1}{E}\right)(\sigma_{zz}-\nu(\sigma_{xx}+\sigma_{yy}))\]
for the z direction.
Similar to the figure below (and discussed in Section 1.1) in these three equations, the subscript \(xx\) indicates a strain or stress in the x direction acting perpendicular to a plane whose normal direction is also in the x direction. You will typically see stress components expressed using either the numbers 1, 2, or 3 or the letters x, y, and z to refer to the orientations of the planes and the forces. It is necessary to know the orientation of the three directions to interpret the orientations of the stresses.

Using Stress to Calculate Strain
The picture below shows the crater wall inside Mt. Vesuvius (this picture was taken from the visitors center on the crater wall). The crater wall is 305 meters high. In Section 1.1 you learned how to calculate the lithostatic stress. Most of the lava erupted from Mt Vesuvius is andesitic in composition with density in the range of 2400 - 2800 kg/m\(^3\). Using an intermediate value of 2600 kg/m\(^3\), the lithostatic stress at the base of the wall is 7.8 MPa.
Now, lets ask how much has the rock been shortened at the base of the wall due to the weight of the rock above?
|
Photo courtesy of M. I. Billen |
To answer this question we will use Equation 1.3.5 to calculate the normal strain in the vertical direction, z. For this equation we need to know the three normal components of stress, as well as the Young's modulus (40 GPa) and Poisson's ratio (0.2) from the tables above (use values for granite). We will use the following values for stress \(\sigma_{zz} = \sigma_{lith}\). This is the lithostatic (vertical) stress. \(\sigma_{xx} = 0\). This is the stress perpendicular to the wall. Since there is air next to the wall this stress is zero. \(\sigma_{yy} = 2 \sigma_{zz}\). For this direction we will assume that the horizontal stress equals twice the vertical stress. Why twice? If the wall was not there the state of stress would that of lithostatic pressure (all normal stresses equal. However since no stress is support in the direction of the wall, we assume that this stress must be supported in the orthogonal direction. With these values, Equation 1.3.5 becomes \(\varepsilon_{zz}=\frac{\sigma_{zz}}{E}(1-2\nu)\) Plugging in values we find, \(\varepsilon_{zz}=\frac{7.8e6}{40e9}(1-2(0.2)) = 0.000117\) To interpret what this value means, we can use the definition of linear strain and solve for the change in length (l-L) assuming the initial length \(L = 305\) m \(l - L = \epsilon_n L = 0.000117*305 = 0.035\) m, or about 3.5 cm Therefore the weight of the rock in the crater wall has elastically shortened (compressed) the rock at the base of the wall by about 3.5 cm. This is elastic strain, so if the rock above were removed, the rock at the base would return to its original size. |



