1.1: Stress
- Page ID
- 3533
Supporting Topics
Prior to reading the page, please review the following topics if you are unfamiliar with them.
Resources for each topic can be found here: Supporting Topics
Calculus
- Vector Components
In introductory physics courses we learn about how objects move when forces act on them. However, we usually consider that the object itself is perfectly rigid and we are not concerned with the internal deformation of the object. However, when we want to consider how an object deforms internally when a force is applied we have to consider the rheology of the material, the orientation of the applied forces, and where these forces are applied. In this section, you will learn how to describe the applied forces acting on an object in terms of the components of stress that exist at a point within the object.
Stress
When a force is applied to a rock it does not act at a single point, but rather over some area. Think about squeezing an eraser between your fingers: the force from your fingers acts over the area of contact between your fingers and the eraser. Stress is the term used to describe the magnitude of the force acting on a surface with some area (Figure \(\PageIndex{1}\)). In other words, stress is force divided by area,
\[\sigma=\frac{F}{A}\]
Since force has units of Newtons (N = \(kg\frac{m}{s^2}\)) and area has units of \(m^2\), stress has units of \(\frac{N}{m^2}\) or in SI (Système International) units \(\frac{kg}{ms^2}\). In geosciences, we typically use the unit Pascal (symbol: Pa) to quantify stress and pressure: 1 Pa = 1 \(\frac{N}{m^2}\).
Components of Stress
A force can be applied to an area at different angles resulting in two different components of stress: normal stress and shear stress. In the example of squeezing an eraser with your fingers, the force is applied perpendicular to, or normal to, the surface of the eraser. Therefore, this stress is termed a normal stress. Normal stress acts at a right angle (perpendicular) to a surface and can either push a rock together (compression) or pull it apart (tension). In geology, compressional stress is positive and tensional stress is negative. In engineering, the opposite sign convention is used. In geological settings compressional stress is typically found in convergent margins where tectonic plates collide. Compressional stress also results from the weight of the rock itself pushing down on the rock below it. Tensional stress is typically found in divergent margins where tectonic plates are being pulled apart.
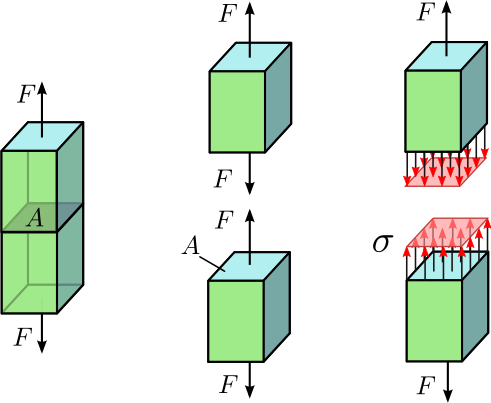
Advanced concept: in the above picture there is a pair of forces with one force acting on each side of the block. Each of these single forces acting on one side of the block or one side of a surface is termed a traction. A pair of tractions acting on opposites sides of a plane is a stress. For certain types of analysis (e.g., a force balance on a portion of a tectonic plate) one needs to consider individual tractions. However, for applications in this text we will only be concerned with stresses.
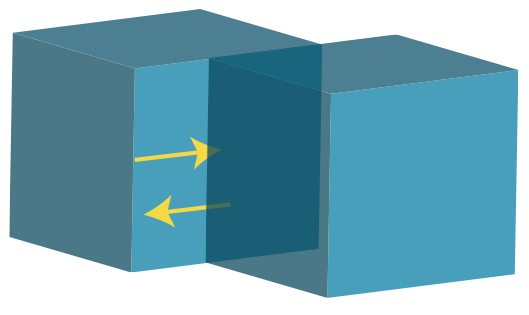
The second type of stress is a shear stress, which is a stress that acts tangential (parallel) to a surface. If you slide your hand across the top of your desk, the resistance you feel is a shear stress between your hand and the desk. Similarly, if you slide two blocks past each other, the frictional resistance to sliding generates a shear stress (Figure \(\PageIndex{2}\)). Shear stresses are typically found on all faults, resulting from the component of the regional stress that acts parallel to the fault surface.
Pressure and Lithostatic Stress
You may have noticed that stress has the same units as pressure, force per unit area. When we normally talk about pressure, we are talking about pressure in a gas (air pressure) or a liquid (the pressure at the bottom of the ocean). Pressure is a special state of stress that occurs when the normal stresses acting at a point are the same in all directions. In this special case there are no shear stresses, only normal stresses, and no matter what direction you measure the stress the value is always the same. Over long periods of time the deep interior of the planet behaves as a fluid, so just like in the ocean we can think about the pressure at a point inside the earth.
In geological applications we are also concerned with pressure in the crust or lithosphere, although it is not expected to find stress-states in the crust or lithosphere (or in the mantle) where the state of stress is simply that of constant pressure. Instead we expect the stress-state to be different in different directions even if there are no applied tectonic forces (see next section about elasticity). Instead, we use pressure as a reference state to which tectonic forces are added. This reference stress-state is referred to as a lithostatic stress or lithostatic pressure. The word lithostatic comes from the word Greek word litho for rock and the term static, meaning not moving.
Lithostatic stress is the stress caused by the weight of the rock above a point. Strictly speaking it is the vertically-oriented normal stress. This is also sometimes referred to as the overburden. The normal stresses in the horizontal directions will normally not be equal to the lithostatic stress. However, in geologic applications we often start analysis from a fictional stress-state of lithostatic pressure. In this case, because we use the word pressure, we are saying that the normal stress in all directions is equal to the lithostatic stress.
When one uses the term lithostatic pressure (or just pressure) there is an implicit assumption that the value of the stress is the same in all directions. Therefore, when considering the state of stress in the crust or lithosphere we often start from a state of lithostatic pressure and then ask what is the magnitude and direction of the stresses acting in addition to the lithostatic pressure.
Calculating Lithostatic Stress
Lithostatic stress is the stress due to the weight (force due to gravity) of the overlying rock. Consider a tall rectangular of rock above a point in the crust. This rectangle has a height, \(h\) and the area of its base is given by \(A = L \times w\). The force due to the weight of the overlying rock is \(F = m a = m g\), where \(m\) is the mass and \(g\) is gravity (9.81 m/s2). The mass is given by the density, \(\rho\) times the volume (\(m = \rho L w h\)). The lithostatic stress at the bottom of the rectangle is
\[\sigma_{lith} = \frac{F}{A} = \frac{m g}{A} = \frac{\rho L w h g}{Lw} = \rho g h\]
Notice that the dimensions of the area of the rectangle do not appear in this equation, even though the units of stress are N\m2. This means that so long as the height and density is constant within the rectangle, the lithostatic stress is the same whether it is calculated for a rectangle with an area the size of a football field or a single point, or any other area. For this reason, we often use a unit rectangle with dimensions of \(1 \times 1\) m2, when doing calculations of stress.
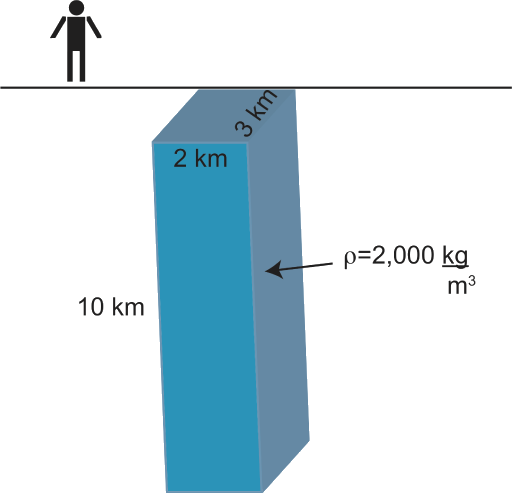
In Figure \(\PageIndex{6}\), the density of the rock is 2000 kg/m3 and the height of the rock is 10 km (10,000 m). The sides of the base of the rectangle are given, but we do not actually need these numbers. Plugging in these numbers to the equation above (note I'm using 10,000 meters so I'm using SI units for all the numbers),
\(\sigma_{lith} = (2000)*(10,000)*(9.81) = 196,200,000\) N/m2
You should always check the units to make sure you have the correct units that you expect. Usually it is good practice to change all your numbers to SI units before plugging in.
\[ \frac{kg}{m^3}*m*\frac{m}{s^2} = \frac{kg}{ms^2} = \frac{N}{m^2} = Pa \nonumber\]
So the lithostatic stress is 196,200,000 Pa. This is a very big number, so instead of using just Pascals, we use mega-Pascals (MPa) or giga-Pascals (GPa) to represent stress.
- 1 MPa = \(10^6\) Pa. (1 million pascals)
- 1 GPa = \(10^9\) Pa. (1 billion pascals)
For this example, it is most appropriate to use MPa because this gives us a number where we don't need to stop and count zeros
\[ \begin{align*} \sigma_{lith} &= 196,200,000~Pa * \frac{1~MPa}{10^6~Pa} \\[4pt] &= 196\, \text{MPa} \end{align*}\]
Choosing whether to use MPa or GPa takes some practice, but usually you want your final answer to be between 0.01 and 9999, so that it is an easy number to read.
3D Stress Components
Generally speaking the stress state at a particular location in the crust, lithosphere or mantle, is not simply described by two opposing stresses, but rather a three-dimensional (3-D) stress state. To completely describe such a 3-D stress state requires three pairs of normal stresses oriented in three orthogonal directions (i.e., x, y, z) and 6 sets of shear stress acting on the planes that are perpendicular to the normal stresses. In the figure below these components are labeled with two numbers (indices). The first number represents the orientation of the surface that the stresses are acting on (1 indicates that the normal to the plane points in the \(x_1\) direction. The second number indicates the direction of the force component acting on the plane. For example, note that all three stresses acting on the plane with an \(x_1\) normal (the front of the box) have 1 as the first index. Stress components with two indices that are the same (e.g. \(\sigma_{11}\) are normal stresses because the force is aligned in the same direction as the normal to the plane). Stress components with two different indices are shear stresses. There are six shear stresses because on one plane there can be a component of shear stress: one in the horizontal direction and one component shear stress in the vertical direction (or any two orthogonal directions on the plane). Note that if the rock is not moving (or we are in a reference frame with the moving rock), then some of the shear stress are equal: \(\sigma_{12} = \sigma_{21}\) and \(\sigma_{13} = \sigma_{31}\) and \(\sigma_{23} = \sigma_{32}\). Therefore, we usually only need to consider 6 independent components of stress. We will return to these stress components in the next section.
Advanced Concept: Such a 3-D stress state can also be completely represented by a special set of three orthogonal normal stresses called principal stresses. The orientation of these three stresses is special because in this particular orientation the shear stress components all have a value of zero (i.e., no shear stress). These principal stress directions are eigenvectors of the stress matrix and the magnitudes of the stress in each direction are the eigenvalues.



