11.2: Absolute Ages of Rocks
- Page ID
- 12709
As we learned in the previous lesson, index fossils and superposition are effective methods of determining the relative age of objects. In other words, you can use superposition to tell you that one rock layer is older than another. But determining the absolute age of a substance (its age in years) is a much greater challenge. To accomplish this, scientists use a variety of evidence, from tree rings to the amounts of radioactive materials in a rock.
Lesson Objectives
- Define the difference between absolute age and relative age.
- Describe four methods of absolute dating.
- Explain what radioactivity is and give examples of radioactive decay.
- Explain how the decay of radioactive materials helps to establish the age of an object.
- Estimate the age of an object, given the half-life and the amounts of radioactive and daughter materials.
- Give four examples of radioactive materials that are used to date objects, and explain how each is used.
Tree Rings
In regions outside the tropics, trees grow more quickly during the warm summer months than during the cooler winter. This pattern of growth results in alternating bands of light-colored, low density “early wood” and dark, high density “late wood”. Each dark band represents a winter; by counting rings it is possible to find the age of the tree (Figure 11.22). The width of a series of growth rings can give clues to past climates and various disruptions such as forest fires. Droughts and other variations in the climate make the tree grow slower or faster than normal, which shows up in the widths of the tree rings. These tree ring variations will appear in all trees growing in a certain region, so scientists can match up the growth rings of living and dead trees. Using logs recovered from old buildings and ancient ruins, scientists have been able to compare tree rings to create a continuous record of tree rings over the past 2,000 years. This tree ring record has proven extremely useful in creating a record of climate change, and in finding the age of ancient structures.

Figure 11.22: Cross-section showing growth rings. The thick, light-colored part of each ring represents rapid spring and summer growth. The thin, dark part of each ring represents slow autumn and winter growth.
Ice Cores and Varves
Several other processes result in the accumulation of distinct yearly layers that can be used for dating. For example, layers form within glaciers because there tends to be less snowfall in the summertime, allowing a dark layer of dust to accumulate on top of the winter snow (Figure 11.23). To study these patterns, scientists drill deep into ice sheets, producing cores hundreds of meters long. Scientists analyze these ice cores to determine how the climate has changed over time, as well as to measure concentrations of atmospheric gases. The longest cores have helped to form a record of polar climate stretching hundreds of thousands of years back.

Figure 11.23: Ice core section showing annual layers.
Another example of yearly layers is the deposition of sediments in lakes, especially the lakes that are located at the end of glaciers. Rapid melting of the glacier in the summer results in a thick, sandy deposit of sediment. These thick layers alternate with thin, clay-rich layers deposited during the winter. The resulting layers, called varves, give scientists clues about past climate conditions. For example, an especially warm summer might result in a very thick layer of sediment deposited from the melting glacier. Thinner varves can indicate colder summers, because the glacier doesn’t melt as much and carry as much sediment into the lake.
Age of Earth

Figure 11.24: Lord Kelvin.
While tree rings and other annual layers are useful for dating relatively recent events, they are not of much use on the vast scale of geologic time. During the 18th and 19th centuries, geologists tried to estimate the age of Earth with indirect techniques. For example, geologists measured how fast streams deposited sediment, in order to try to calculate how long the stream had been in existence. Not surprisingly, these methods resulted in wildly different estimates, from a few million years to “quadrillions of years”. Probably the most reliable of these estimates was produced by the British geologist Charles Lyell, who estimated that 240 million years have passed since the appearance of the first animals with shells. Today scientists know his estimate was too young; we know that this occurred about 530 million years ago.
In 1892, William Thomson (later known as Lord Kelvin) calculated the age of Earth in a systematic fashion (Figure 11.24). He assumed that the Earth began as a ball of molten rock, which has steadily cooled over time. From these assumptions, he calculated that the Earth was 100 million years old. This estimate was a blow to geologists and supporters of Charles Darwin’s theory of evolution, which required an older Earth to provide time for evolution to take place.
Thomson’s calculations, however, were soon shown to be flawed when radioactivity was discovered in 1896. Radioactivity is the tendency of certain atoms to decay into lighter atoms, emitting energy in the process. Radioactive materials in Earth’s interior provide a steady source of heat. Calculations of Earth’s age using radioactive decay showed that Earth is actually much older than Thomson calculated.
Radioactive Decay
The discovery of radioactive materials did more than disprove Thomson’s estimate of Earth’s age. It provided a way to find the absolute age of a rock. To understand how this is done, it is necessary to review some facts about atoms.
Atoms contain three particles: protons, neutrons, and electrons. Protons and neutrons are located in the nucleus, while electrons orbit around the nucleus. The number of protons determines which element you’re examining. For example, all atoms of carbon have six protons, all atoms of oxygen have eight protons, and all atoms of gold have 79 protons. The number of neutrons, however, is variable. An atom of an element with a different number of neutrons is an isotope of that element. For example, the isotope carbon-12 contains 6 neutrons in its nucleus, while the isotope carbon-13 has 7 neutrons.
Some isotopes are radioactive, which means they are unstable and likely to decay. This means the atom will spontaneously change from an unstable form to a stable form. There are two forms of nuclear decay that are relevant in how geologists can date rocks (Table (11.1):
| Particle | Composition | Effect on Nucleus |
|---|---|---|
| Alpha | 2 protons, 2 neutrons | The nucleus contains two fewer protons and two fewer neutrons. |
| Beta | 1 electron | One neutron decays to form a proton and an electron, which is emitted. |
If an element decays by losing an alpha particle, it will lose 2 protons and 2 neutrons. If an atom decays by losing a beta particle, it loses just one electron.
So what does this have to do with the age of Earth? Radioactive decay eventually results in the formation of stable daughter products. Radioactive materials decay at known rates. As time passes, the proportion of radioactive isotopes will decrease and the proportion of daughter isotopes will increase. A rock with a relatively high proportion of radioactive isotopes is probably very young, while a rock with a high proportion of daughter products is probably very old.
Scientists measure the rate of radioactive decay with a unit called half-life. The half-life of a radioactive substance is the amount of time, on average, it takes for half of the atoms to decay. For example, imagine a radioactive substance with a half-life of one year. When a rock is formed, it contains a certain number of radioactive atoms. After one year (one half-life), half of the radioactive atoms have decayed to form stable daughter products, and 50% of the radioactive atoms remain. After another year (two half-lives), half of the remaining radioactive atoms have decayed, and 25% of the radioactive atoms remain. After the third year (three half-lives), 12.5% of the radioactive atoms remain. After four years (four half-lives), 6.25% of the radioactive atoms remain, and after 5 years (five half-lives), only 3.125% of the radioactive atoms remain.
If you find a rock whose radioactive material has a half life of one year and measure 3.125% radioactive atoms and 96.875% daughter atoms, you can assume that the substance is 5 years old. The decay of radioactive materials can be shown with a graph (Figure 11.25). If you find a rock with 75% of the radioactive atoms remaining, about how old is it?
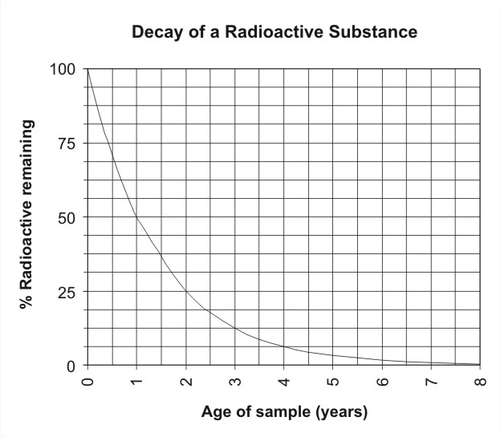
Figure 11.25: Decay of an imaginary radioactive substance with a half-life of one year.
Radiometric Dating of Rocks
In the process of radiometric dating, several isotopes are used to date rocks and other materials. Using several different isotopes helps scientists to check the accuracy of the ages that they calculate.
Carbon Dating
Earth’s atmosphere contains three isotopes of carbon. Carbon-12 is stable and accounts for 98.9% of atmospheric carbon. Carbon-13 is also stable and accounts for 1.1% of atmospheric carbon. Carbon-14 is radioactive and is found in tiny amounts. Carbon-14 is produced naturally in the atmosphere when cosmic rays interact with nitrogen atoms. The amount of carbon-14 produced in the atmosphere at any particular time has been relatively stable through time.
Radioactive carbon-14 decays to stable nitrogen-14 by releasing a beta particle. The nitrogen atoms are lost to the atmosphere, but the amount of carbon-14 decay can be estimated by measuring the proportion of radioactive carbon-14 to stable carbon-12. As a substance ages, the relative amount of carbon-14 decreases.
Carbon is removed from the atmosphere by plants during the process of photosynthesis. Animals consume this carbon when they eat plants or other animals that have eaten plants. Therefore carbon-14 dating can be used to date plant and animal remains. Examples include timbers from an old building, bones, or ashes from a fire pit. Carbon dating can be effectively used to find the age of materials between 100 and 50,000 years old.
Potassium-Argon Dating
Potassium-40 decays to argon-40 with a half-life of 1.26 billion years. Because argon is a gas, it can escape from molten magma or lava. Therefore any argon that is found in a crystal probably formed as a result of the decay of potassium-40. Measuring the ratio of potassium-40 to argon-40 will yield a good estimate of the age of the sample.
Potassium is a common element found in many minerals such as feldspar, mica, and amphibole. The technique can be used to date igneous rocks from 100,000 years to over a billion years old. Because it can be used to date geologically young materials, the technique has been useful in estimating the age of deposits containing the bones of human ancestors.
Uranium-Lead Dating
Two isotopes of uranium are used for radiometric dating. Uranium-238 decays to form lead-206 with a half-life of 4.47 billion years. Uranium-235 decays to form lead-207 with a half-life of 704 million years.
Uranium-lead dating is usually performed on crystals of the mineral zircon (Figure 11.26). When zircon forms in an igneous rock, the crystals readily accept atoms of uranium but reject atoms of lead. Therefore, if any lead is found in a zircon crystal, it can be assumed that it was produced from the decay of uranium.

Figure 11.26: Zircon crystal.
Uranium-lead dating can be used to date igneous rocks from 1 million years to around 4.5 billion years old. Some of the oldest rocks on Earth have been dated using this method, including zircon crystals from Australia that are 4.4 billion years old.
Limitations of Radiometric Dating
Radiometric dating can only be used on materials that contain measurable amounts of radioactive materials and their daughter products. This includes organic remains (which compared to rocks are relatively young, less than 100,000 years old) and older rocks. Ideally, several different radiometric techniques will be used to date the same rock. Agreement between these values indicates that the calculated age is accurate.
In general, radiometric dating works best for igneous rocks and is not very useful for determining the age of sedimentary rocks. To estimate the age of a sedimentary rock deposit, geologists search for nearby or interlayered igneous rocks that can be dated. For example, if a sedimentary rock layer is sandwiched between two layers of volcanic ash, its age is between the ages of the two ash layers.
Using a combination of radiometric dating, index fossils, and superposition, geologists have constructed a well-defined timeline of Earth history. For example, an overlying lava flow can give a reliable estimate of the age of a sedimentary rock formation in one location. Index fossils contained in this formation can then be matched to fossils in a different location, providing a good age measurement for that new rock formation as well. As this process has been repeated all over the world, our estimates of rock and fossil ages has become more and more accurate.
Lesson Summary
Techniques such as superposition and index fossils can tell you the relative age of objects, which objects are older and which are younger. Other types of evidence are needed to establish the absolute age of objects in years. Geologists use a variety of techniques to establish absolute age, including radiometric dating, tree rings, ice cores, and annual sedimentary deposits called varves.
Radiometric dating is the most useful of these techniques—it is the only technique that can establish the age of objects older than a few thousand years. The concentrations of several radioactive isotopes (carbon-14, potassium-40, uranium-235 and -238) and their daughter products are used to determine the age of rocks and organic remains.
Review Questions
- What four techniques are used to determine the absolute age of an object or event?
- A radioactive substance has a half-life of 5 million years. What is the age of a rock in which 25% of the original radioactive atoms remain?
- Figure 11.27: Radioactive decay of Carbon-14
- Which radioactive isotope or isotopes would you use to date each of the following objects? Explain each of your choices.
- A 4 billion year old piece of granite.
- A one million year old bed of volcanic ash that contains the footprints of hominids (human ancestors).
- The fur of a woolly mammoth that was recently recovered frozen in a glacier.
- A fossilized trilobite recovered from a bed of sandstone that is about 500 million years old.
- The principle of uniformitarionism states that the present is the key to the past. In other words, the processes that we see happening today probably worked in a similar way in the past. Why is it important to assume that the rate of radioactive decay has remained constant over time?
Vocabulary
- absolute age
- The age of an object in years.
- alpha particle
- Particle consisting of two protons and two neutrons that is ejected from the nucleus during radioactive decay.
- beta particle
- Particle consisting of a single electron that is ejected from the nucleus during radioactive decay. A beta particle is created when a neutron decays to form a proton and the emitted electron.
- daughter product
- Stable substance that is produced by the decay of a radioactive substance. For example, uranium-238 decays to produce lead-207.
- half-life
- Amount of time required for half of the atoms of a radioactive substance to decay and form daughter products.
- ice core
- Cylinder of ice extracted from a glacier or ice sheet.
- radioactive
- Substance that is unstable and likely to emit energetic particles and radiation.
- radioactivity
- Emission of high-energy particles and/or radiation by certain unstable atoms.
- radiometric dating
- Process of using the concentrations of radioactive substances and daughter products to estimate the age of a material. As substances age, the amounts of radioactive atoms decrease while the amounts of daughter materials increase.
- tree ring
- Layer of wood in a tree that forms in one year. You can determine the age of a tree by counting its rings.
- varve
- Thin layer of sediment deposited on a lakebed over the course of one year usually found at the bottom of glacial lakes.
Points to Consider
- Why are techniques like tree rings, ice cores, and varves only useful for events that occurred in the last few thousand years?
- Why was it so important for Darwin and his followers to prove that the Earth was very old?
- Why is it important to use more than one method to find the age of a rock or other object?
- Provided by: Wikipedia. Located at: http://en.wikibooks.org/wiki/High_School_Earth_Science/Absolute_Ages_of_Rocks. License: CC BY-SA: Attribution-ShareAlike

