14.5: Deviations from the Condition of Equal Mobility
- Page ID
- 4243
Some perspective is needed at this point. You have seen, from discussion of the various data sets presented in the preceding sections, that although the thresholds and transport rates of mixed-size sediments show a much closer approach to the condition of equal mobility than to the condition of gradation independence, there remains a deviation from the condition of equal mobility such that in general the coarser fractions are somewhat more difficult to entrain and transport than the finer fractions; in other words, the combined effects of hiding–sheltering and rollability are insufficient to counteract fully the effect of particle weight.
The incomplete approach to the condition of equal mobility leads to two related concepts: selective entrainment and partial transport. The term selective entrainment refers to differences in movement thresholds among the various size, shape, and density fractions of a sediment consisting of a mixture of particle sizes, shapes and densities. The emphasis here is on size-selective entrainment, although density-selective entrainment is one of the keys to the development of placers. Much of the work on selective entrainment is owing to Komar (1987a, 1987b, 1989).
A concept related to that of selective entrainment is that of partial transport: for a range of bed shear stresses above the condition of no particle movement, a given size fraction may comprise two populations:
- Particles that are moved, occasionally, by the flow; and
- Particles that are never moved by the flow, and remain motionless on the bed (Wilcock and McArdell, 1993, 1997).
The domain of partial transport lies between the range of bed shear stresses for which there is no motion of any of the particles of the given size fraction, on the one hand, and the range of greater bed shear stress for which all of the particles of the given size fraction are moved by the flow at one time or another. In general, the lower and upper limits of this range differ from size fraction to size fraction. A corollary is that, when all of the size fractions are considered, the domain of partial transport extends from the upper limit of bed shear stress for which no particles of any size fraction are moved by the flow, on the one hand, and the lower limit of bed shear stress for which at least some of the particles of all of the size fractions are moved at one time or another, on the other hand.
What is the relationship between partial transport and fractional transport rates? Insight into that question comes from flume experiments on partial transport by Wilcock and McArdell (1993, 1997). The sediment was unimodal but poorly sorted mixture with the distinctive feature that all of the particles of each of the size fractions was painted a different color, to facilitate observations of particle immobility and particle movement on the sediment bed. Observations of partial transport, as well as fraction transport rates, were made in several runs over a range of bed shear stress that bracketed the domain of partial transport as described above.
Figure \(\PageIndex{1}\), a plot of fractional transport rate against particle size, shows the relationship between partial transport and fractional transport rates for each of five runs. In Figure \(\PageIndex{1}\) the limiting value of the active proportion of particles in each size fraction, after a long running time, is denoted by \(Y_{i}\). Each data point in Figure \(\PageIndex{1}\) represents a given size fraction in a given one of the five runs. The proportion of the particles of the given fraction that are mobile increases from lower right to upper left for each curve.
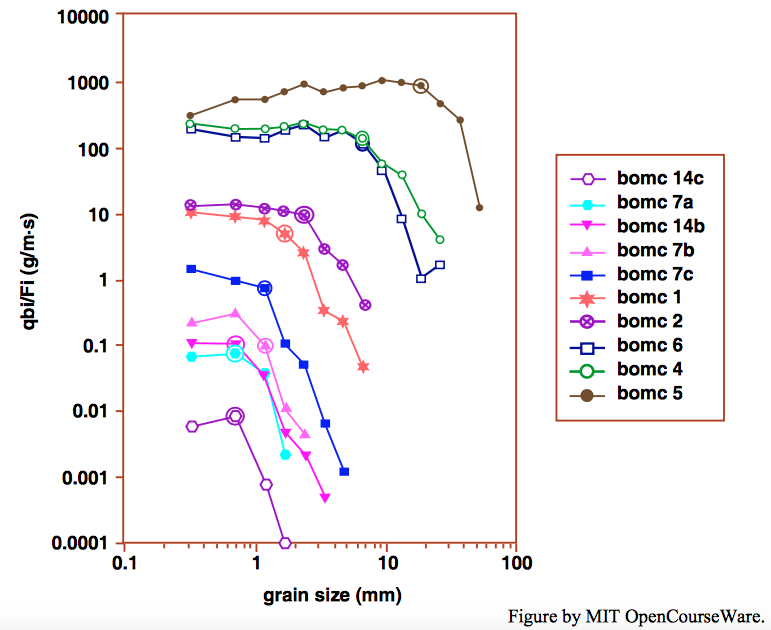
The distinctive feature of the plot in Figure \(\PageIndex{1}\) is that the curves for fractional transport rate flatten to near horizontality (a condition approaching equal mobility) as flow strength increase. In other words, deviations from equal mobility are large within the domain of partial transport but become small for bed shear stresses above the domain of partial transport.
More on Sediment-Discharge Formulas: Subsurface-Based Models versus Surface-Based Models
All sediment-discharge formulas, including those described briefly in Chapter 13, make use, in one way or another, of the sediment size, usually the median size. Some such approaches have attempted to deal with mixed-size sediments by introducing a “hiding function” that takes account of the hiding– sheltering effect, but even those need to be based on a particular size distribution of the sediment.
The question then arises: which size distribution should be used? That of the sediment in the substrate, or that of the bed surface, which the flow actually sees? The latter would seem to be the more natural choice. As you have seen, in mixed-size sediments, especially those with both sand and gravel fractions, the sediment bed surface tends to become paved with sediment that is, on average, coarser than the substrate sediment. The problem is that the surface size distribution is itself a function of the flow. Moreover, only in carefully designed laboratory flume experiments is it possible to observe the surface size distribution, and only a few studies have succeeded in doing so. Up to now, only a few transport models based on the surface size distribution rather than the substrate distribution have been developed (Proffitt and Sutherland, 1983; Parker, 1990; Wilcock and Crowe, 2003).
Chapter 14 References Cited
Day, T.J., 1980, A study of the transport of graded streams: Wallingford, U.K., Hydraulics Research Station, Report IT 190.
Dhamotharan, S., Wood, A, and Parker, G., 1980, Bedload transport in a model gravel stream: University of Minnesota, St. Anthony Falls Hydraulics Laboratory, Project Report 190.
Milhous, R.T., 1973, Sediment transport in a gravel-bottomed stream: Ph.D. thesis, Oregon State University, Corvallis, Oregon.
Misri, R.L., Garde, R.J., and Ranga Raju, K.G., 1984, Bed load transport of coarse nonuniform sediment: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 110, p. 312-328.
Parker, G., 1990, Surface-based bedload transport relation for gravel rivers: Journal of Hydraulic Engineering, v. 28, p. 417-436
Parker, G., and Klingeman, P.C., 1982, On why gravel bed streams are paved: Water Resources Research, v. 18, p. 1409-1423.
Parker, G., Dhamotharan, S., and Stefan, S, 1982a, Model experiments on mobile, paved gravel bed streams: Water Resources Research, v. 18, p. 1395-1408.
Parker, G., Klingeman, P.C., and McLean, D.L., 1982b, Bedload and size distribution in paved gravel-bed streams: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 108, p. 544-571.
Proffitt, G.T., and Sutherland, A.J., 1983, Transport of non-uniform sediments: Journal of Hydraulic Research, v. 21, p. 33-43.
Wilcock, P.R., 1987, Bed-load transport of mixed-size sediment: Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts.
Wilcock, P.R., and Crowe, J.C., 2003, Surface-based transport model for mixed-size sediment: Journal of Hydraulic Engineering, v. 129, p. 120-128.
Wilcock, P.R., and McArdell, B.W., 1993, Surface-based fractional transport rates: Mobilization thresholds and particle transport of a sand–gravel sediment: Water Resources Research, v. 29, p. 1297-1312.
Wilcock, P.R., and McArdell, B.W., 1997, Partial transport of a sand/gravel sediment: Water Resources Research, v. 33, p. 235-245.
Wilcock, P.R., and Southard, J.B., 1988, Experimental study of incipient motion in mixed-size sediments: Water Resources Research, v. 24, p. 1137-1151
Wilcock, P.R., and Southard, J.B., 1989, Bed load transport of mixed size sediment: fractional transport rates, bed forms, and the development of a coarse bed surface layer: Water Resources Research, v. 25, p. 1629-1641.


