12.3: Velocity Profiles over Ripples
- Page ID
- 4227
The material in the latter part of Chapter 4 on velocity profiles over rough beds is useful here in dealing with vertical profiles of time-average velocity over fields of ripple-shaped bed forms, large or small. It is natural to think about such profiles in two different ranges of height above the bed: well above the ripples, and close to the bed.
Think first about the velocity profile above a plane parallel to the mean bed level and one to two ripple heights above the ripple crests. Unless the ripple height is such a large fraction of the flow depth that the whole flow accelerates and decelerates as it passes over the ripples, such a velocity profile is almost the same wherever it is taken, because at this height the upward-diffusing wake turbulence generated by flow separation at ripple crests is well blended spatially. In the following paragraphs we will use the adjective integrated for such profiles (cf. Paola, 1983). These profiles characterize layers of the flow that blanket entire fields of bed forms without varying at the scale of those bed forms.
First we need to do a little more with velocity profiles near the bed in dynamically rough flows, as a continuation of Chapter 4. This additional material deals with the inner layer not far above the tops of the particles, which we skipped in Chapter 4.
For sand-size bed roughness the lowermost part of the inner layer, not far above the tops of the grains, is not much more than a few millimeters thick, but for water flowing over gravels or for wind blowing over large ground-surface roughness it may be decimeters or even meters thick, and no sophisticated, miniaturized velocity meters are needed to include it in measured velocity profiles. At positions this close to the bed there is a troublesome problem that we have avoided up to now: where is the origin for \(y\)? It seems reasonable to suppose that the \(y = 0\) level lies somewhere between the bases and the tops of the surface particles. A natural choice would be the average surface elevation—the spatial average of the heights, normal to the mean plane of the bed, at which a solid surface is first encountered in descending onto the bed. You will see, however, that this does not produce the best fit of velocity to Equations 4.7.20 or 4.7.21 of Chapter 4. And it is not a very practical choice anyway. With close-packed granular roughness, the plane through the tops of the grains (which itself is not very well defined) is usually taken as the \(y = 0\) level for velocity measurements.
For a given dimensionless distance \(y^{+}\) from the boundary, \(u/u_{*}\) is not the same in rough and smooth flow, because the second term on the right side of Equation 4.7.13 always has a value different from B in Equation 4.7.14. But the shape and slope of the velocity profile are the same: if you differentiate Equation 4.7.13 for the rough-flow velocity profile with respect to \(y\), you get
\[\frac{d u}{d y}=\frac{A u_{*}}{y} \label{12.11}\]
which is exactly the same as Equation 4.7.12 for flow over a smooth bottom. You might expect, however, that, at positions closer down to the tops of the grains, the grains have some effect on the shape as well as the position of the velocity profile, making the shape different from the smooth-flow case. In other words, when \(y\) is not much greater than \(D\), the velocity gradient depends not only on \(\tau_{\text{o}}\), \(\rho\), and \(y\) but also on \(D\):
\[\frac{d u}{d y}=f\left(\tau_{o}, \rho, y, D\right) \label{12.12} \]
or in dimensionless form,
\[\frac{u}{u_{*}} \frac{d u}{d y}=f\left(\frac{D}{y}\right) \label{12.13} \]
It is convenient to extract the same constant \(A\) from the function on the right in Equation \ref{12.13}, so that the effect of proximity to the bed grains can be viewed as a correction function by which the right side of Equation \ref{12.11} must be multiplied:
\[\frac{d u}{d y}=\frac{A u_{*}}{y} f\left(\frac{D}{y}\right) \label{12.14} \]
There is no simple way of dealing with the physics behind the correction function \(f(D/y)\) in Equation \ref{12.14}. The only thing we can say with certainty is that as \(y\) gets smaller (and \(D/y\) gets larger) the correction gets larger. To investigate the correction function further we can expand it as a power series in \(D/y\) (Monin and Yaglom, 1971; remember that any function can be approximated in this way by an appropriate power series.) Equation \ref{12.14} can then be written
\[\frac{d u}{d y}=\frac{A u_{*}}{y}\left[1+a \frac{D}{y}+b\left(\frac{D}{y}\right)^{2}+\ldots\right] \label{12.15}\]
As the boundary is approached from above, and the correction gets larger, the term \(a(D/y)\), the dominant term while the correction is still small, gets less important relative to terms of higher order in \(D/y\). In the following we will consider only positions higher than one to two diameters above the tops of the roughness elements. Measurements are seldom made closer to the bed anyway, because to get a representative value for the mean velocity a large number of profiles must be taken at different places relative to the roughness elements and then spatially averaged.) To conform to the usual practice in dealing with the grain-proximity correction, we will recast Equation \ref{12.15} into a slightly different form by introducing a new variable \(y-y_{1}\) for the vertical coordinate, where \(y_{1}\) is a small constant that’s in the same ballpark as \(D\) itself. We also need the following algebraic identity:
\[\frac{1}{y}=\left(\frac{1}{y-c}\right)\left(\frac{y-c}{y}\right)=\left(\frac{1}{y-c}\right)\left(1-\frac{c}{y}\right) \label{12.16} \]
where \(y\) is some variable and \(c\) is a constant. Then, replacing \(1/y\) in Equation \ref{12.15} with the right side of the identity above and letting the constant be \(y_{1}\),
\(\frac{d u}{d y}=\frac{A u_{*}}{y-y_{1}}\left(1-\frac{y}{y_{1}}\right)\left[1+\mathrm{a} \frac{D}{y}+\mathrm{b}\left(\frac{D}{y}\right)^{2}+\ldots\right]\)
\[=\frac{A u_{*}}{y-y_{1}}\left(1-\frac{y_{1}}{y}+a_{y}^{D}+\text{terms in} \frac{1}{y^{2}} \text { etc. }\right) \label{12.17} \]
Neglecting terms of order higher than \(1/y\) on the right side, Equation \ref{12.17} becomes
\[\frac{d u}{d y}=\frac{A u_{*}}{y-y_{1}}\left(1+\frac{a D-y_{1}}{y}\right) \label{12.18} \]
We are at liberty to adjust the definition of \(y_{1}\) at the outset in such a way that \(y_{1} = aD\); then Equation \ref{12.18} becomes
\[\frac{d u}{d y}=\frac{A u_{*}}{y-y_{1}} \label{12.19} \]
Equation \ref{12.19} can be integrated in the same way as the rough-flow equivalent of Equation 4.7.12 in Chapter 4 to be in the same form as Equation 4.7.14,
\[\frac{u}{u_{*}}=A \ln \frac{y-y_{1}}{D}+B^{\prime} \label{12.20} \]
and Equation \ref{12.20} can be manipulated into the same form as Equation 4.7.22 in Chapter 4, with \(y_{\text{o}}\) and no separate constant of integration,
\[\frac{u}{u_{*}}=A \ln \frac{y-y_{1}}{y_{\text{o}}} \label{12.21} \]
Equations \ref{12.20} and \ref{12.21} are the conventional way of dealing with the correction function \(f(D/y)\) that appears in Equation \ref{12.14}. Shifting the origin of the \(y\) coordinate by the small quantity \(y_{1}\) usually straightens out the velocity profile in a semilog plot down to positions not far above the tops of the roughness elements. What is commonly done with wind-velocity profiles above the land surface is to take \(y = 0\) at the base of the roughness elements—the ground on which the observer is standing—and then find the value of \(y_{1}\) which when subtracted from \(y\) gives the best straight-line fit of data to Equation \ref{12.21}. The distance \(y_{1}\) (often denoted by \(d\)) is called the displacement height or the zero-plane displacement. The situation is a little different with close-packed granular roughness, which is of greater interest here: usually the velocity profile is measured with respect to the tops of the grains, and then the apparent origin for \(y\) is lowered to produce the best straight-line fit to Equation \ref{12.21}. (The plane through the tops of the grains is not ideally well defined, but it is impossible to define a dynamically natural plane that represents the bases of the grains in a full bed of loose sediment.) So the value of \(y_{1}\) depends not only on the physics of the problem but also on the \(y\) origin chosen at the outset. For a wide variety of roughness geometries, the distance \(y_{1}\) has been found to be between \(0.2\) and \(0.4\) roughness diameters below the tops of the roughness elements (Jackson, 1981).
The physical significance of the displacement height \(y_{1}\) has never been clear. There is some experimental evidence that the height \(y_{1}\) above the origin is the level in the flow at which the boundary shear stress \(\tau_{\text{o}}\) appears to act (Thom, 1971). The horizontal component of the force per unit area the flow exerts on its bed has not only a magnitude but also a line of action. In other words, if we could measure τo with enough accuracy and detail we would find that it appears to act on some plane parallel to the bed. (Presumably this plane would lie somewhere between the bases and tops of the roughness elements.) Choose an arbitrary plane above or below the bed and find the moment \(M\) per unit bed area associated with the force \(\tau_{\text{o}}\) per unit bed area. Dividing \(M\) by \(\tau_{\text{o}}\) gives a quantity with the dimensions of length, and this length is just the distance above or below the arbitrary plane at which \(\tau_{\text{o}}\) acts. Jackson (1981) reasons that this distance is none other than the displacement height \(y_{1}\).
Now, finally, back to velocity profiles over bed forms. In the following, the subscript \(t\) denotes variables associated with the total bed shear stress, and the subscript \(s\) denotes variables associated with the skin friction. If the flow depth is large relative to the ripple height the lower part of the integrated profile (and with little error the upper part also) is well described by Equation \ref{12.21}, the law of the wall for rough boundaries written here using the subscript \(t\),
\[\frac{u}{\left(u_{*}\right)_{t}}=A \ln \frac{y-\left(y_{1}\right)_{t}}{\left(y_{o}\right)_{t}} \label{12.22} \]
The boundary shear stress \(\left(\tau_{\text{o}}\right)_{t}\) concealed in \(\left(u_{*}\right)_{t}\) in Equation \ref{12.22} is the total shear stress the flow exerts on the rippled bed. If you were to invent a good way of measuring pressure and viscous shear stress at every point on the bed, you would have to average over an area much larger than the scale of the ripples to get a representative value for \(\left(\tau_{\text{o}}\right)_{t}\). Most of \(\left(\tau_{\text{o}}\right)_{t}\) is from drag exerted on the ripples, not local stress exerted on the granular bed surface—called skin friction. This latter skin-friction component of the total drag would be largely viscous drag, if flow in the immediate vicinity of the bed is dynamically smooth, or it may itself be largely form drag, if the flow in the vicinity of the bed is dynamically rough. By analogy with the results in Chapter 4 for granular roughness, the roughness length \(\left(y_{\text{o}}\right)_{t}\) associated with the integrated velocity profile in Equation \ref{12.22} is proportional to the height of the ripples and is a small fraction thereof, the exact value depending on the shape (and most importantly the steepness) of the ripples. The displacement height \(\left(y_{1}\right)_{t}\) is such that the origin for the velocity profile lies somewhat below the ripple crests. As the ratio of flow depth to ripple height decreases (but not to the point where there is no longer an integrated profile) it becomes more difficult to distinguish between inner and outer layers of the flow, but the wall-law representation is still a good approximation.
Now look at the velocity profile near the bed at points on the stoss surface of a given ripple. At points well downstream from reattachment the velocity profile near the bed follows the law of the wall also, because of the upward development of the internal boundary layer at the expense of the turbulent wake downstream of separation. If the boundary Reynolds number based on the skin friction \(\left(\tau_{\text{o}}\right)_{s}\) and the local granular roughness height is larger than about \(10\) the flow in the internal boundary layer is dynamically rough, and the velocity profile is given by
\[\frac{u}{\left(u_{*}\right)_{s}}=A \ln \frac{y-\left(y_{1}\right)_{s}}{\left(y_{o}\right)_{s}} \label{12.23} \]
where \(\left(\tau_{\text{o}}\right)_{s}\) in the shear velocity \(\left(u_{*}\right)_{s}\) is a local boundary shear stress that can be viewed as averaged over an area that is large compared with the granular roughness but small compared with the ripples themselves. We will use the adjective local for profiles of this kind, because they apply only to particular points on the ripple. The profile in Equation \ref{12.23} is characterized by values of roughness length \(\left(y_{\text{o}}\right)_{s}\) and displacement height \(\left(y_{1}\right)_{s}\) associated with the granular roughness, and both of these are smaller than the corresponding values associated with the integrated wall-law profile in Equation \ref{12.22}.
If the local boundary Reynolds number is much smaller, less than about \(5\), the local velocity profile is represented instead by the law of the wall for smooth flow, Equation 4.7.6 in Chapter 4,
\[\frac{u}{\left(u_{*}\right)_{S}}=A \ln \frac{\rho\left(u_{*}\right)_{S} y}{\mu}+B \label{12.24} \]
where \(B\) has a value of about \(5.1\), as noted in Chapter 4. In this case the skin friction on the stoss surface of the ripple is mostly viscous drag rather than granular form drag. At intermediate boundary Reynolds numbers the velocity profile is represented by the law of the wall for transitionally rough flow. This can be put into the same form as the rough-flow profile, Equation \ref{12.23}, but with \(y_{n}\) then a function of the local boundary Reynolds number as well as the roughness height, and the skin friction is partly viscous drag and partly form drag. Whether the local flow in the growing boundary layer is smooth or rough, however, \(\left(u_{*}\right)_{s}\) in Equations \ref{12.23} or \ref{12.24} is much smaller than \(\left(u_{*}\right)_{t}\) in Equation \ref{12.22}, because whatever its nature the skin friction on the ripple surface is much smaller than the form drag on the ripples.
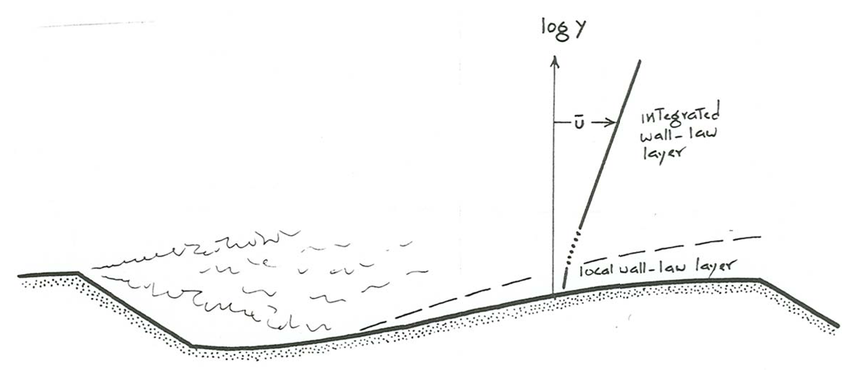
The local wall-law profile varies with distance up the stoss surface: as the flow in the internal boundary layer accelerates up the slope, the skin friction \(\left(\tau_{\text{o}}\right)_{s}\) increases, as does the height to which the profile is applicable. You can be sure, however, that in a simple dimensional semilog plot with \(\log y\) on the vertical axis and \(u\) on the horizontal axis the slopes of the straight lines that represent the local wall-law profile are always much greater than the slope of the single straight line for the integrated wall-law profile that holds well above the level of the crests of the ripples, because \(\left(u_{*}\right)_{t}\) is much larger than \(\left(u_{*}\right)_{s}\); see Figure \(\PageIndex{1}\), which summarizes the relationship between the integrated profile and the local profile above a given point on the stoss surface of a ripple. In between the regions of applicability of the local wall-law profile near the bed and the integrated wall-law profile well above the ripples is a complicated region of the flow in which the velocity grades from one profile to the other. This region thins downstream along the stoss surface but is not consumed completely even when the flow reaches the next ripple crest downstream.
Where small dunes are superimposed on much larger dunes, the foregoing line of reasoning can be taken a step further. Large internal boundary layers develop on the stoss surfaces of the larger dunes in just the same way that small internal boundary layers develop on the smaller dunes. The smaller dunes, of which there presumably are a great number on the stoss face of each larger dune, act as local roughness beneath the internal boundary layer that develops up the stoss surface of each larger dune. There is therefore a layer of the flow well above the crests of the smaller dunes but still well below the crests of the larger dunes in which the velocity follows an intermediate wall-law profile (Figure \(\PageIndex{2}\)). This intermediate profile looks simultaneously like an integrated (although slowly varying) profile to a small observer stationed on one of the smaller dunes but like a local profile to a large observer stationed on one of the larger dunes. This profile is characterized by values of \(u_{*}\), \(y_{\text{o}}\), and \(y_{1}\) intermediate between those of the integrated profile over the large dunes and those of the local profile over the smaller dunes. From the standpoint of the large dunes the intermediate value of \(u_{*}\) represents a local boundary shear stress, so in a sense it is skin friction even though form drag predominates over viscous drag. At the same time, the viscous drag and smaller-scale form drag associated with the sediment grains on the surfaces of the smaller dunes represent skin friction relative to the smaller dunes.
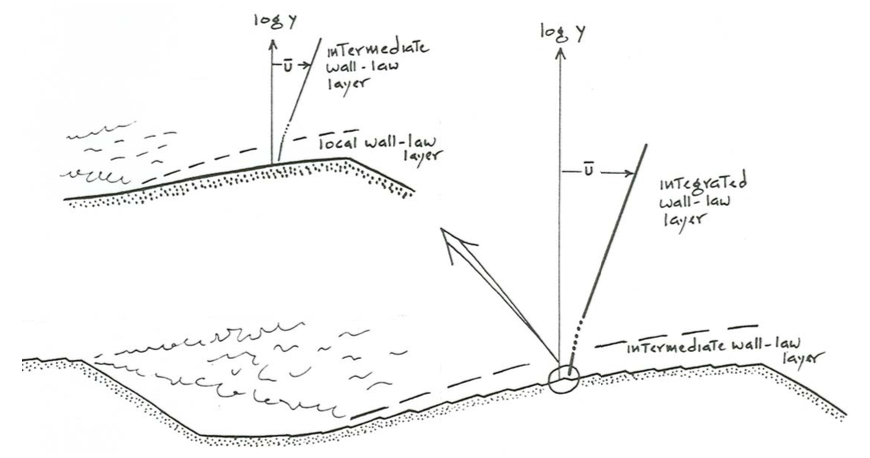
The same ideas can even be extended to very large dunes (which many would call sand waves) on which two orders of smaller dunes with two greatly different scales are superimposed. There are then two different intermediate layers of the flow, of the kind just described, each with its own wall-law profile characterized by its own set of values of \(u_{*}\), \(y_{\text{o}}\), and \(y_{1}\): one that is local relative to the largest dunes (the sand waves themselves) but integrated relative to the larger superimposed dunes and one that is local relative to the larger superimposed dunes but integrated relative to the smaller superimposed dunes.
You could take velocity profiles at a large number of points along the profile of one or more of the largest dunes present on the bed and average them all together to obtain a spatially averaged velocity profile. In a sense this spatially averaged profile represents the entire flow. Such averaging is not entirely satisfactory, for two reasons:
- Owing to growth of the internal boundary layer, the near-bed part of the velocity profile varies with position along the dune profile (even aside from the gross changes caused by separation and reattachment in the vicinity of the trough).
- Because the origin plane for the integrated wall-law region associated with dunes of a given order is parallel to the mean plane of the bed in the vicinity of those dunes, whereas the origin for the individual profiles is naturally taken at the bed surface itself, the base of the integrated wall-law profile is encountered at different heights in different places. The latter problem is not as serious as it seems, however, because at the height of even the lowest of such integrated wall- law regions, points at rather different heights plot close to each other on a logarithmic vertical axis. Provided that the ratio of spacing to height of the dunes of each order is large, so that separation bubbles occupy only a small fraction of the area of the bed, the spatially averaged profile in a semilog plot of height against velocity shows a series of straight-line segments connected by smooth transitions, just like the individual profiles—although the transitions are likely to be more gradual, for the two reasons noted above. The values for boundary shear stress obtained from these straight-line segments in the spatially averaged profile represent the spatial averages of the boundary shear stresses associated with each order of bed form present, ranging upward in scale from the grain roughness itself. For further details on such spatially averaged velocity profiles over dunes, see Smith and McLean (1977).


