8.1: Introduction to Sediments, Variables, and Flumes

Introduction

In the natural sciences, the word sediment is used for loose particulate material at the Earth’s surface that has been produced by weathering of rocks and then transported by wind or water or ice. Because weathering acts everywhere to some degree, and the Earth is enveloped by moving air and water, it should not surprise you that sediment is ubiquitous. In engineering applications, the word “sediment” is used to refer not only to natural sediment but also to particulate material, of whatever origin, that is transported (or just potentially transportable) in some flow device or system.

The dynamics of sediment transport is a large field, which is of interest in a wide variety of disciplines in the Earth sciences and engineering: geology, geomorphology, geography, oceanography, environmental science and engineering, civil engineering, mechanical engineering, and chemical engineering. Civil engineering has probably had more impact on the development of ideas and techniques in sediment transport mechanics than any other single discipline.

In Part 2 of these notes I will deal with some of the most important phenomena and problems connected with the transport of denser solid particles by turbulent flow of a less dense fluid, which in most cases of interest is water or air. Emphasis will be on

• the forces exerted on the sediment particles by the flowing fluid
• the modes of movement of the particles by the flow, and
• the shaping of a loose sediment bed by the flow.

The greatest emphasis will be on flows in which the concentration of transported sediment is low enough that the turbulence structure of the flow—and the approach we can take to the dynamics of the flow itself—is not grossly different from flows without sediment. Flows with greater concentrations, sometimes approaching the limiting concentration of close packing of the sediment particles, are important in both natural sciences and engineering, but the limited scope of these notes precludes treatment here—they should be the topic of an entire additional set of notes.

Sediment

Before we get started on sediment movement, I will point out some useful things to know about the sediment itself. These have to do with the size, shape, and density of the material.

The picture I want you to have is of what might be called a “gravity bed” of loose sediment particles: the particles are denser than the fluid, and they form a bottom boundary to the flow, below which the mass of particles rests packed together in a framework that is stable against the pull of gravity (Figure \(\PageIndex{1}\)). We will be dealing with the uppermost part of this bed, where the particles are accessible to the flow—by which I mean that if not actually in motion at a given time, they are resting on the bed surface, or are located at a depth below the sediment–fluid interface small enough that the flow can (and presumably will, at some time) erode to that depth, given enough time even without any change in the overall or average flow conditions. This uppermost layer of potentially movable sediment is usually called the active layer.

Figure \(\PageIndex{1}\): A “gravity bed” of loose sediment particles.

Each bed particle is characterized by a size, a shape, and a density. Density is the simplest to deal with: the mean density of a particle is just the ratio of its mass to its volume. Size and shape are more difficult to deal with.

Size would be a straightforward concept only if the particle had the shape of a regular geometric solid. Some particles approach spherical shape, but most are irregular in shape. A theoretically satisfying measure of the size of an irregular particle is its nominal diameter: the diameter of a sphere with the same volume as the given particle. You can imagine, however, the difficulty you would have in measuring the nominal diameter of a sand grain! What is done is to define and measure size operationally: the meaning of size lies in how we actually measure it. The size of sediment coarser than about \(0.1\) \(\mathrm{mm}\) is usually measured by passing it though a sieve with nearly square openings formed by a grid of (usually) metal wire. Approximately speaking, a sieve discriminates size by passing all particles whose longest dimension in the smallest cross-sectional area is about that of the size of the sieve opening.

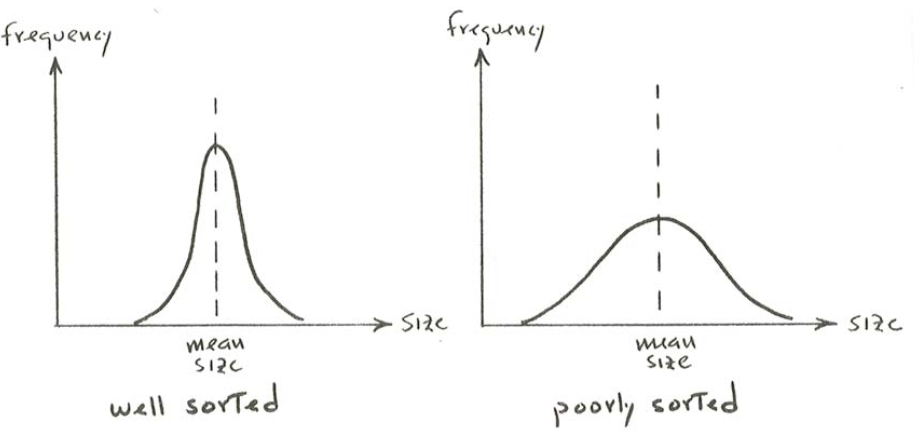
All natural sediments have a range of particle sizes. The spread of sizes around the average size is called the sorting: a well sorted sediment shows a narrow spread of sizes, and a poorly sorted sediment shows a wide spread of sizes (Figure \(\PageIndex{2}\)). (In civil engineering practice, the terminology is just the opposite: a well sorted sediment is poorly graded, and a poorly sorted sediment is well graded.) The effect of sorting on sediment transport is a rapidly advancing area of research nowadays.

Figure \(\PageIndex{2}\): Sorting: the spread of sizes around the mean.

Shape is even more difficult to deal with than size. Clearly, natural sediment particles with their irregular shapes would require an enormous number of separate and independent variables to describe the shape: a hopeless situation. Fairly well-rounded sediment particles are often approximated by triaxial ellipsoids, which need only two ratios among three independent variables (longest axis, intermediate axis, and shortest axis) to characterize the shape.

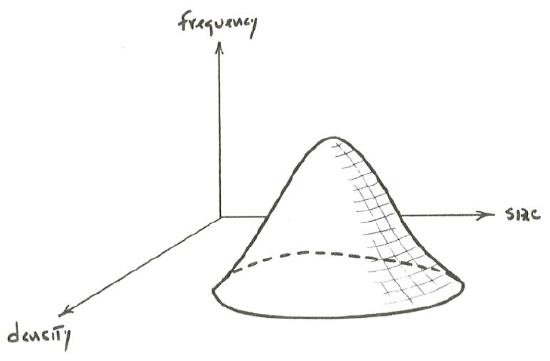
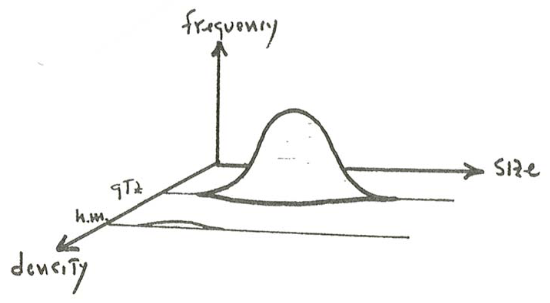
Even though we will not be dealing with anything but a single sediment density and an average sediment size in the following, it does not hurt to keep in mind always that a natural sediment has a three-dimensional joint distribution of size, shape, and density, which always has to be approximated in some way, and always very crudely. That joint distribution has too many axes for me to draw, but Figure \(\PageIndex{3}\) shows a simpler two-dimensional joint frequency distribution of size and density, with shape ignored. We can do better than Figure \(\PageIndex{3}\), though: most natural sediments have a dominant density fraction associated with quartz, feldspar, rock fragments, and carbonate particles, and a subordinate fraction consisting of a variety of heavy minerals with much greater density (Figure \(\PageIndex{4}\)).

Figure \(\PageIndex{3}\): A joint frequency distribution of sediment size and sediment density.

Figure \(\PageIndex{4}\): What the joint size–density frequency distribution looks like for many natural sediments.

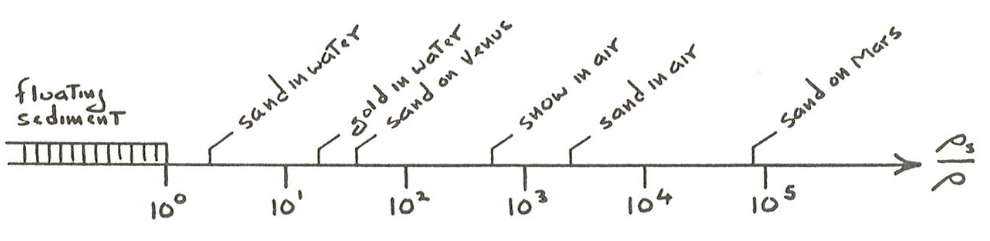
The ratio of particle density to fluid density ranges enormously in natural sediment-transporting flows, from winds on Mars to water flows on Earth (Figure \(\PageIndex{5}\)). The important points along this spectrum for us earthling sedimentologists are for quartz-density and heavy-mineral sediments in water and air. But we must not be presumptuous: think of all the places there must be in the universe where sediment is being moved, at this very moment, for which the density ratio is greatly different from these few particular cases of greatest interest to us. It is wise for sediment dynamicists to keep a broad perspective, because otherwise, in concentrating on just a few cases some important general effects might be misinterpreted, or even missed.

Figure \(\PageIndex{5}\): The spectrums of density ratios \(\rho\)