7.2: The Coriolis Effect on the Earth's Surface
- Page ID
- 4191
Fluid flows you observe on the Earth’s surface experience a Coriolis acceleration. That is because the Earth is rotating, and both you and the flowing fluid are rotating with it. The effects you discovered on your turntable show up in those flows as well. The only places this should seem really obvious to you are at the North Pole and the South Pole—where the Earth’s surface is perpendicular to the axis of rotation. But the Coriolis acceleration affects fluid motions everywhere else on the Earth’s surface also.
The complete mathematical development of the Coriolis effect, although straightforward, would take us too far off the path of these notes, so I will give you an abbreviated and incomplete picture, just for the flavor.
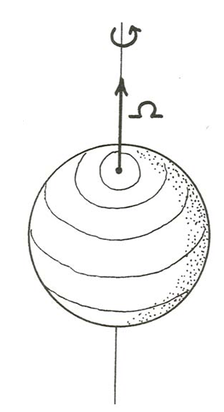
I mentioned above that the rate of rotation of a rotating body is denoted by \(\omega\). But to be specific about such a rotation, you need to describe the orientation and the sense of the rotation as well. The rotation of the Earth is described by its angular velocity—a vector, denoted by \(\Omega\), lying within the axis of rotation and with length equal to the rate of rotation \(\omega\). By convention, the angular velocity vector points north to express the sense of rotation of the Earth, which is counterclockwise when viewed from above the North Pole (Figure \(\PageIndex{1}\)). The angular velocity \(\Omega\) thus specifies the orientation, sense, and rate of rotation of the Earth.
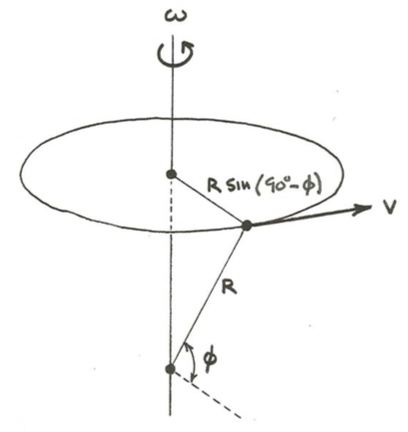
Look at a point on the Earth’s surface. The speed \(v\) of that point, relative to outer space, is equal to the angular velocity \(\omega\) times the distance from the rotation axis to the point. Expressed in terms of the radius \(R\) of the Earth and the latitude angle \(\phi\), this can be written \(R \omega \sin \left(90^{\circ}-\phi\right)\) (Figure \(\PageIndex{2}\)).
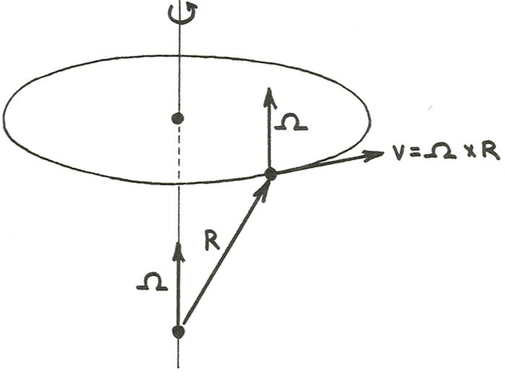
A more elegant way of looking at the movement of a point on the Earth’s surface is to characterize the position of the point by a position vector \(r\) that stretches from the center of the Earth to the given point (Figure \(\PageIndex{3}\)) and then express the velocity of the point as \(\boldsymbol{v}=\boldsymbol{\Omega} \times \boldsymbol{r}\). The product on the right side is a cross product of vectors, defined so that the result has a magnitude \(r \omega \sin \left(90^{\circ}-\phi\right)\), which is the same as the result in the last paragraph, because \(r = R\). Note that the vector product is itself a vector; the vector product is arranged so that its direction and sense correctly describe the velocity of the given point on the Earth’s surface. Note also that \(v\) is normal to both \(\Omega\) and \(r\); that is one of the properties of the cross product.
Now look at a little marker particle moving along with the air of the atmosphere or the water of the ocean. That particle has its own velocity relative to the solid Earth; call that velocity \(v_{R}\), where the subscript \(R\) is meant to suggest that the velocity is relative to the rotating Earth. The motion of the particle can also be viewed from outer space; call its velocity relative to that “fixed” frame of reference \(v_{I}\), where the subscript \(I\) stands for inertial, an adjective that in physics is associated with a frame of reference that is not accelerating. It should make good sense to you that
\[\boldsymbol{v}_{\boldsymbol{I}}=\boldsymbol{v}_{\boldsymbol{R}}+\boldsymbol{\Omega} \times \boldsymbol{r} \label{7.1} \]
Equation \ref{7.1} just tells you that the absolute velocity of the moving particle is the sum of its velocity relative to the rotating Earth plus the rotational velocity of the point, stationary relative to the Earth, past which the particle happens to be moving at a given time.
The complications begin when we look at the acceleration of the marker particle, not just its velocity. The acceleration of the particle is the time rate of change of its velocity. To find the acceleration you have to differentiate the vector \(v_{I}\) with respect to time, and then, for use of the result in our rotating earthly frame of reference, express the result in terms of quantities like \(v_{R}\) that are observed from within that rotating frame of reference. I will just cite the result for \(a_{I}\), the acceleration of the particle relative to the outer-space reference frame:
\[\boldsymbol{a_{I}} = \boldsymbol{a_{R}}+2 \boldsymbol{\Omega} \times \boldsymbol{v_{R}}+ \boldsymbol{\Omega} \times \boldsymbol{\Omega} \times \boldsymbol{r}+\frac{d \boldsymbol{\Omega}}{d t} \times \boldsymbol{r} \label{7.2} \]
where \(a_{R}\) is the acceleration of the particle as observed from the rotating Earth. (For details, see Pedlosky, 1987, Chapter 1.)
There are four terms on the right side of Equation \ref{7.2}. The first, \(a_{R}\), is easy to understand, but the other three need some explanation. The fourth expresses the effect of time rate of change of the rotation rate; it is something we need not worry about for geophysical flows. The third is the centripetal acceleration, with which you are all familiar in at least a qualitative way: if you tie a rope around a boulder and swing it around in a big circle, you are producing a centripetal (“center-seeking”) acceleration of the boulder, arising from the inward-directed radial force you are exerting on the boulder to constrain it to travel in a circular arc rather than go off straight on its own. The second term is the one we are after in this exercise: it is the Coriolis acceleration.
Look more closely at the Coriolis acceleration term in Equation \ref{7.2}. First of all, it is a vector itself, because it is a cross product of two vectors. Its magnitude is a linear function of the magnitude of the velocity \(v_{R}\): the faster the particle moves, the larger the Coriolis acceleration. Also, its magnitude depends not only on the magnitude of \(v_{R}\) but also on the direction of \(v_{R}\) relative to the Earth’s axis. In every case, though, the direction of the Coriolis acceleration is normal to vR itself (remember the properties of the cross product), and that is consistent with what you learned about the Coriolis acceleration on your big turntable.
A good way to study the effects of the Coriolis acceleration on fluids moving at the Earth’s surface is to look at a particular point on the Earth’s surface at a particular latitude \(\phi\) (Figure \(\PageIndex{4}\)). To a local observer the situation there looks planar, so think about a plane that is tangent to the Earth’s surface at the given point. I will call that the horizontal plane, because it is horizontal at the tangent point. The motions of both the atmosphere and the oceans most affected by the Coriolis acceleration are almost entirely horizontal flows: broad-scale vertical motions in the atmosphere and oceans are usually of far smaller velocity than horizontal motions, and locally strong vertical motions, as within cloud convection cells, are on space and time scales for which the Coriolis effect turns out to be unimportant.
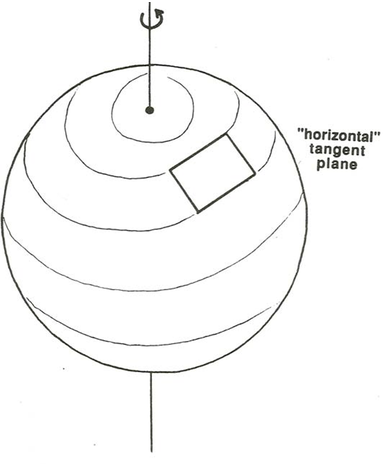
In the horizontal plane it is natural to set up a coordinate system with one axis vertical, one in the direction of movement of the particle, and the other horizontal and normal to the direction of movement (Figure \(\PageIndex{5}\)). And the Coriolis acceleration itself can be resolved into components in those three directions (Figure \(\PageIndex{6}\)). Think just about the horizontal components of the Coriolis acceleration, because they are what are important for the horizontal motions of fluids; it is easy to show that the vertical component of the Coriolis force in a vertical flow is swamped by the balance between the two large vertically acting forces—pressure and gravity—and is therefore negligible.
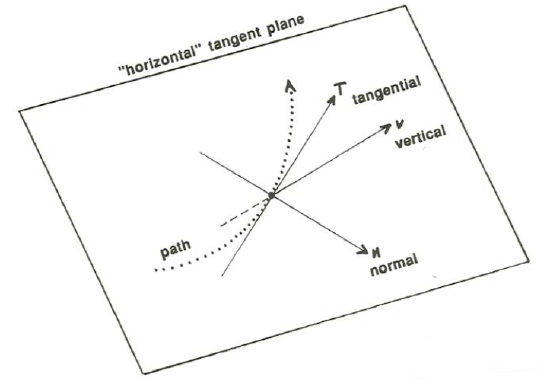

You have already seen that the component of the Coriolis acceleration in the direction of movement, the \(t\) axis in Figure \(\PageIndex{6}\), is always zero. What we need to worry about is the magnitude of the horizontal component of the Coriolis acceleration in the direction normal to the horizontal movement, and how it varies with both latitude and the direction of movement within the horizontal plane. I will do this in a shortcut way by looking at two special directions, north–south and east–west.
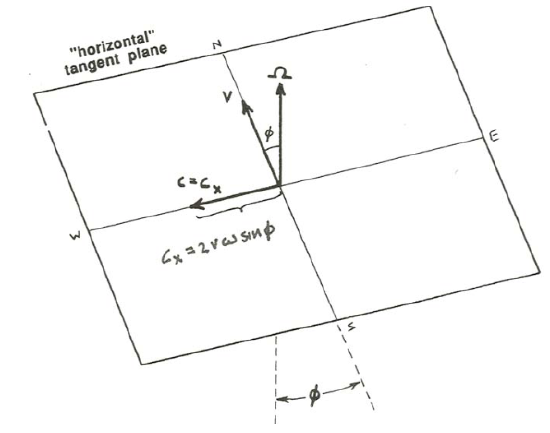
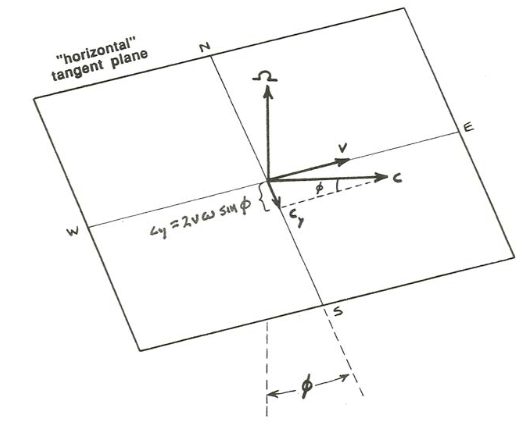
Look at the east–west orientation first. The Coriolis acceleration is directed normal to both \(v\) and \(\Omega\), which to an observer on the horizontal plane is a vector that sticks up into the sky toward the south and at an angle to the horizontal that is equal to \(90^{\circ}\) minus the latitude angle \(\phi\). By reference to Figure \(\PageIndex{7}\), if you resolve that vector into the horizontal plane the component has the magnitude 2\(v \omega \sin \phi\). Now look at the north–south orientation. To an observer on the horizontal plane the Coriolis acceleration vector is horizontal and points due east for a northward movement and due west for a southward movement. By reference to Figure \(\PageIndex{8}\), the magnitude of the Coriolis acceleration is again 2\(v \omega \sin \phi\). Although the mathematics is much more intricate, it turns out that the Coriolis acceleration has this same magnitude, 2\(v \omega \sin \phi\), for any direction of movement in the horizontal plane.
So the bottom line on the Coriolis acceleration for horizontal movements on the Earth’s surface is this:
- Its magnitude is directly proportional to the speed of the body,
- Its horizontal component is always directed normal to the direction of movement (to the right in the Northern Hemisphere but to the left in the Southern Hemisphere), and
- Its magnitude is always 2\(v \omega \sin \phi\).
So the Coriolis effect is largest at the poles and zero at the Equator. (It works just the opposite way for the vertical component of the Coriolis acceleration—largest at the Equator—but, as I said before, the vertical component is unimportant anyway.) What is usually done with this expression for the Coriolis acceleration is to extract the 2\(v \omega \sin \phi\) part and call it the Coriolis parameter, denoted by \(f\).
Finally, I want to make sure that you do not confuse the separate effects of the centripetal acceleration and the Coriolis acceleration, both of which affect the motion of bodies on the Earth’s surface as viewed by an observer on the Earth. The centripetal acceleration affects all bodies in and on the Earth, whether they are stationary or moving. To reveal its effect, go back to your turntable and place a big shallow pan of water on it. You know what happens when the table is rotated: the water banks up against the outer side of the pan, and the inward-sloping water surface sets up a horizontal component of the gravity force that counterbalances the outward centrifugal force. After the initial adjustment in water-surface slope is made, the centrifugal force has no further direct effect on the movement of the water relative to an observer riding on the turntable. (Lakes and oceans on Earth adjust in this same way—as does the solid Earth itself. It is the reason why the Earth is an oblate spheroid, with equatorial diameter larger than pole-to-pole diameter, rather than a sphere.) Because the velocity of the water relative to the boundaries of the pan is zero, there is no Coriolis acceleration.
Now move your hand in the water to produce a gentle current in the interior of the water in the pan. Of course the pattern of flow will be modified by friction and eventually die away, but while the water is moving it experiences the Coriolis acceleration, and the configuration of the current is more or less strongly affected, depending upon the speed of the water and the rate of rotation of the turntable. It is these effects in the atmosphere and oceans that we are going to investigate in the rest of this chapter.


