6.3: Water Motions Due to Waves

The aspect of surface gravity waves that is relevant to sediment movement lies largely in the back-and-forth movement of the water at the bottom: are those oscillatory currents strong enough to entrain bottom sediment? To get at the nature of bottom water motions under oscillatory waves, it is best to start with small-amplitude wave theory. The most far-reaching progress in theory of water waves came about by making the assumption that the wave steepness \(H/L\) is so small that the convective accelerations (like \(u \partial u / \partial x\)) in the equation of motion can be neglected compared to the local accelerations (like \(\partial u / \partial t\)). It turns out that this assumption simplifies the equation to such an extent that an exact solution can be obtained, by methods beyond the scope of these notes. Such waves are called Airy waves, after the person who first developed the solution.

It turns out that the small-amplitude solution holds to good approximation for values of wave steepness \(H/L\) well beyond what we have any right to expect. So we can get a good idea of the behavior of finite-amplitude waves just by relying on the small-amplitude solution.

What the solution gives us is the fluid velocity and fluid pressure at every point, and the geometry of the water surface, all a function of time. The water motions below the surface, and especially near the bottom, are of greatest interest in sediment transport.

As an oscillatory wave passes by, each little element or parcel of the water undergoes a closed-loop trajectory or orbit, making one traverse of that orbit as each wave form passes. As your intuition might tell you, the diameter of the orbits decreases with depth below the free surface. This makes sense, because the water-surface disturbance is generated and maintained at the surface by the forces of the wind on the water.

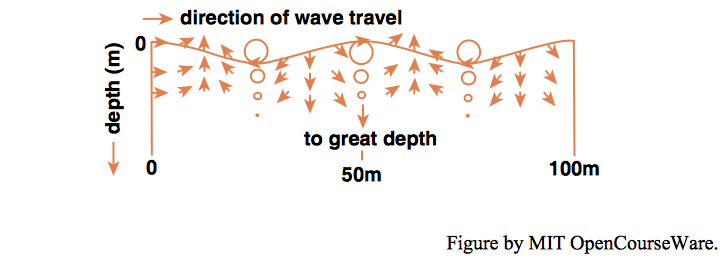
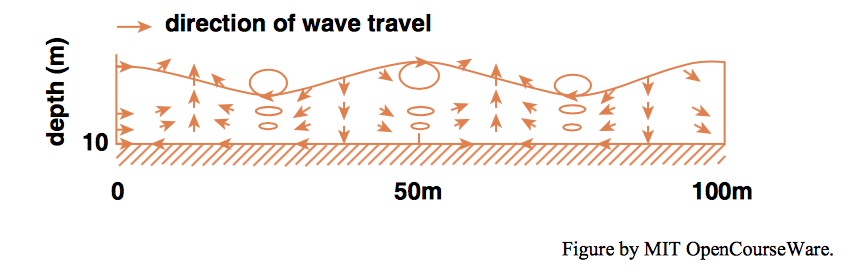
In deep-water waves, for which \(L/d\) is very small, the orbits are everywhere nearly circular, and the size of the orbits decreases sharply with increasing depth until they are negligible at depths equal to only one wavelength (Figure \(\PageIndex{1}\)). The orbits are perfectly circular only in the limit of vanishingly small \(H/L\), but even for non-negligible \(H/L\) the orbits are very close to being circular. In shallower water the passage of the waves causes water motions all the way to the bottom, although except at the largest values of \(L/d\) the diameter of the orbits still decreases with depth. The orbits even at the surface are somewhat elliptical, flattened in the vertical, and they become more elliptical with depth, until at the bottom they are back-and forth straight lines (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{1}\): Instantaneous velocity vectors at a given time, and orbital paths of fluid particles over one complete cycle, in a wave motion in deep water. (From Neumann and Pierson, 1966.)

Figure \(\PageIndex{2}\): Instantaneous velocity vectors at a given time, and orbital paths of fluid particles over one complete cycle, in a wave motion in water of constant shallow depth. Approximate conditions are shown for a wave with amplitude of \(2.5 \mathrm{m}\) and a wavelength of \(50 \mathrm{m}\) in water \(10 \mathrm{m}\) deep. (From Neumann and Pierson, 1966.)

The effect of finite wave steepness is to distort the wave form such that crests are sharper and troughs are broader, and to distort the orbits such that the speeds are greater when the water is moving in the direction of wave propagation than in the direction opposite wave propagation. (But the net transport remains nearly zero, because the time during which the higher forward speeds prevail are shorter than the times during which the lower reverse speeds prevail.)

The size of wind-generated surface gravity waves depends on three things: wind speed, duration, and fetch. It is obvious to even the most casual observer that wave size increases with wind speed. The reason is that the wind transfers some of its kinetic energy to the waves, both by shear stresses on the water surface and by the front-to-back pressure differences you learned about in Chapter 3, and this adds mechanical energy to the waves, in the form of kinetic energy of the water motions in the wave and potential energy associated with elevation differences of the undulatory water surface. But the waves are not created instantly by the wind: it takes time for the waves to build to a state of equilibrium with the wind. One or both of two processes eventually begin to dissipate the energy of the waves:

1. Breaking of the wave crests (called whitecapping), as the waves become steeper, which converts the organized mechanical energy of the waves to turbulence and thence to heat; and
2. If the wave are large enough relative to the water depth, bottom friction, which bleeds off energy at the bottom of the water column, in the oscillatory-flow boundary layer (more on that later) and converts it to heat.

The term fetch is used for the distance over which the wind can work on the waves. You know, from standing at the shore of the ocean or a lake with the wind blowing offshore, that the waves grow from little ripples to much larger waves in the offshore direction, ultimately to reach equilibrium with the wind if the fetch is long enough.

If you, as an otherwise knowledgeable sedimentationist, were approaching the problem of bottom water movement by waves for the first time, one of the first things that would occur to you would probably be to ask how to predict the nature of the bottom water motions as a function of the wind speed. The bottom water motions might be characterized by the oscillation period \(T\), the size of the excursions of water elements near the bottom, called the orbital diameter \(d_{\text{o}}\), or the maximum near-bottom water velocity during one oscillation period, which I will denote by \(U_{m}\). These three quantities are not independent of one another: they are related by the equation \(U_{m}T = \pi d_{\text{o}}\). You might try your hand at deriving this simple relationship sometime, when you have some time to spare.

Unfortunately there is no simple way to make such a prediction, because it depends on the balance, mentioned above, between energy input from the wind and energy dissipation both at the surface, by whitecapping, and at the bottom, by bottom friction. One thing, albeit only qualitative, that can be said is that the shallower the water depth, the more important the bottom friction is in determining the balance. In very deep water its role is non-existent, whereas in very shallow water it becomes the dominant effect. Where the water is sufficiently shallow that a wind with effectively unlimited fetch has produced a fully developed wave state, such that energy loss by bottom friction does not allow the waves to grow any larger, the sea state has been called a depth-limited sea. Such wave states must be common in the shallow ocean during powerful storms, and much of the work of the waves on the sediment bottom takes place at those times.

It is easy to make a regular train of waves in a wave tank: all you need to do is put a wave generator of some kind in one end (a flap that is hinged at the bottom and moved back and forth in simple harmonic motion at the top does nicely) and energy-absorbing material at the other end, to prevent reflection of the incoming waves. You know, however, that waves that have attained equilibrium with a wind, or are building toward equilibrium, are far less regular: the crests are not regular and straight-crested, and if you try to watch a single wave crest as it progresses, it soon disappears, to be replaced by other wave crests. The explanation is that the wave state actually is a combination, or superposition, of a set of “component” waves, each with a slightly different period, speed, and direction of propagation. The reality of these component waves is manifested not in the region of wave generation but along distant shores. You are at the beach, during a nice settled spell of summer weather, watching the waves come into shore and break on the beach. Close observation would reveal that these waves, called swell, come from a single direction and are very regular in their size and period. These are waves that were generated by some distant storm and have crossed a great expanse of open ocean to arrive at your beach. Deep-water waves are said to be dispersive: the Airy wave solution, mentioned above, for the speed of deep-water waves is \(c^{2}=g L / 2 \pi\), where \(c\) is the wave speed and \(L\) is the wavelength of the waves. That means that longer waves outrun shorter waves, to arrive at distant locations earlier. And the waves sort themselves out by direction as well. It is those two effects—dispersion and directionality—that make the incoming swell so regular.

In the midst of a storm at sea, however, matters are different: the sea state comprises a range of wave sizes and directions, making for a complicated surface topography. Such a wave state is usually represented by what is called a two-dimensional wave spectrum, and the waves are referred to as spectral waves. Think in terms of a joint frequency distribution of wave energy in terms of wave period (or wave frequency) and direction. The sea state generated by a wind that blows in one direction for a long time shows a very elongated distribution, with a wide range of periods but a much narrower range of directions, but if the wind direction is changing, as commonly happens during the passage of a storm, the wave state has to readjust, and while it does so the two-dimensional wave spectrum is likely to broad in direction as well as in period.

The relevance of the wave spectrum is that it translates to what the water motions are at depth, although the picture of motions at depth is mediated, or filtered, by the rapid decrease in amplitude of the component wave motions with depth. Because of this rapid decrease, the water column acts as a kind of low-pass filter, emphasizing the contribution of the larger wave components at the expense of the smaller, thus making the water motions at the bottom less variable, in both period and orientation, than at the surface. Even so, during strong but changing winds you might expect the water motions at the bottom to be not as simple as a regular back-and-forth motion with a single orientation.