3.9: Settling of Spheres
- Page ID
- 4808
Introduction
This section deals with some basic ideas about settling of solid spheres under their own weight through still fluids. This is an important topic in meteorology (hailstones), sedimentology (sediment grains), and technology (cannon balls and spacecraft). In this section we will look at the terminal settling velocity of spheres as an applied problem. At the end I will make some comments about the complicated matter of the time and distance it takes for a sphere to attain its terminal settling velocity.
If placed in suspension in a viscous fluid, a solid body denser than the fluid settles downward and a solid body less dense than the fluid rises upward. A qualification is needed here, however: the body must not be so small that its submerged weight is even smaller than the random forces exerted on it by bombardment by the fluid molecules in thermal motion. Such small weights are generally associated only with the finest particles, in the colloidal size range of small fractions of a micron.
When a nonneutrally buoyant body is released from rest in a still fluid, it accelerates in response to the force of gravity. As the velocity of the body increases, the oppositely directed drag force exerted by the fluid grows until it eventually equals the submerged weight of the body, whereupon the body no longer accelerates but falls (or rises) at its terminal velocity, also called the fall velocity or settling velocity in the case of settling bodies (Figure \(\PageIndex{1}\)).
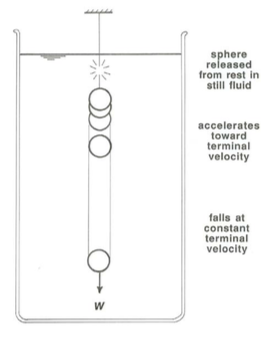
Towing vs. Settling
I promised you in Chapter 2 that I would make some comments later about the differences between moving a sphere through still fluid and passing a moving fluid by a stationary sphere. This topic has relevance to the settling of spheres, so I will say some things about it at this point.
It should make sense to you that towing a sphere at velocity \(U\) through a still fluid by exerting a constant force \(F_{D}\) on it is equivalent to passing a steady and uniform stream of fluid at velocity \(U\) around a sphere that is held fixed relative to the boundaries of the flow. This is largely true, but there are two complications. First, if the sphere is held fixed and the flow passes by it, the drag force can be influenced by even weak turbulence in the approaching flow, whereas if the sphere is towed through still fluid there can be no such effect. Second, you have seen that, in some ranges of relative velocity, eddies can form behind the sphere and break away irregularly; if the sphere is fixed and the fluid is flowing by, this causes the force to fluctuate about some average value but does not affect the relative velocity, whereas if the sphere is towed, either the velocity fluctuates along with the force or, if by definition we tow with a constant force, the velocity fluctuates but the force is steady.
Settling of a sphere through still fluid under its own weight is exactly like towing the sphere vertically downward by applying a constant towing force, namely the weight of the sphere, which is simply the Earth’s gravitational attractive force on the sphere. The weight of the sphere is constant and entirely independent of the state of motion, and the sphere responds by settling downward at some velocity through the fluid. (As noted above, this velocity may fluctuate slightly with time.) For spheres the differences between the fixed-sphere case and the settling-sphere case are usually assumed to be minor. Indeed, some of the data in Figure 2.3.1 for dimensionless drag force as a function of Reynolds number are from settling experiments and some are from wind-tunnel experiments with fixed spheres, and it can be seen that there is very little scatter of the combined experimental curve.
Dimensional Analysis
To obtain an experimental curve for settling velocity we can simply transform the curve in Figure 2.3.1 for drag coefficient vs. Reynolds number for towed spheres into a curve based on settling velocity. In fact, much of this curve, especially for low Reynolds numbers, was obtained by settling experiments in the first place, with the experimental results recast into the form of drag coefficients.
When a sphere falls at terminal velocity the drag force \(F_{D}\) is equal to the submerged weight of the particle, \((1 / 6) \pi D^{3} \gamma^{\prime}\), where \(\gamma^{\prime}\) is the submerged weight per unit volume of the particle, equal to \(g\left(\rho_{s}-\rho\right)\). Substituting this for \(F_{D}\) in the definition of the drag coefficient \(C_{D}\) in Equation 2.3.2, using settling velocity \(w\) in place of \(U\), and then solving for \(C_{D}\),
\[C_{D}=\frac{4}{3} \frac{\gamma^{\prime} D}{\rho w^{2}} \label{3.22} \]
This expression for \(C_{D}\), which can be viewed as the “settling drag coefficient”, can be used in the relationship for dimensionless drag force as a function of Reynolds number (Equation 2.3.2) for spheres moving through a viscous fluid:
\[\frac{\gamma^{\prime} D}{\rho w^{2}}=f\left(\frac{\rho w D}{\mu}\right) \label{3.23} \]
where the factor \(4/3\) has been absorbed into the function, just for convenience. Figure \(\PageIndex{2}\), which is the same as Figure 2.3.1 with axes relabeled and adjusted in scale to take account of the factor \(4/3\), is the corresponding graph of this function. No data points are shown, because the curve is exactly the same as in Figure 2.3.2. Figure \(\PageIndex{2}\) gives settling velocity was an implicit function of \(\rho\), \(U\), \(D\), and \(\gamma^{\prime}\).
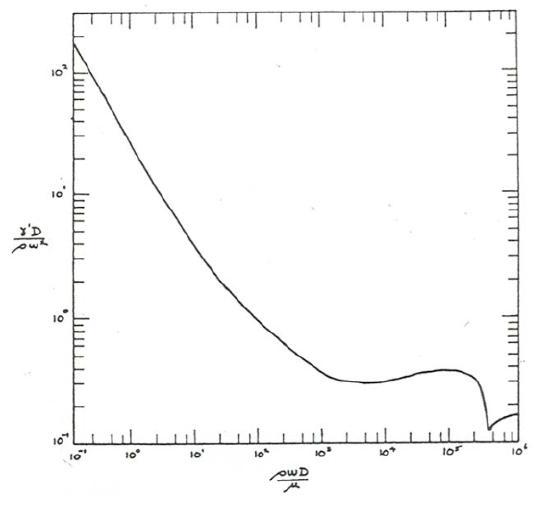
The curve in Figure \(\PageIndex{2}\) is still not very convenient for finding the settling velocity when the other variables are given. This is because both \(w\) and \(D\) appear in the dimensionless variables along both axes. Finding \(w\) in an actual problem would necessitate laborious trial-and-error computation. To get around this problem the graph can be further recast into a more convenient form in which \(w\) appears in only one of the two dimensionless variables. Also, because usually what is desired is \(w\) as a function of \(D\), or vice versa, it is convenient to arrange for \(D\) to appear only in the other variable.
Recall from Chapter 2 that if you have a set of dimensionless variables for a problem you can multiply or divide any one of them by any others in the set to get a new variable to replace the old one. To get a dimensionless variable with \(w\) but not \(D\), invert the left-hand variable in Equation \ref{3.23} and multiply the result by the right-hand variable:
\[\left(\frac{\rho w^{2}}{\gamma^{\prime} D}\right)\left(\frac{\rho w D}{\mu}\right)=\frac{\rho^{2} w^{3}}{\gamma^{\prime} \mu} \label{3.24} \]
And to get a dimensionless variable with \(D\) but not \(w\), square the right-hand variable in Equation \ref{3.23} and multiply it by the left-hand variable:
\[\left(\frac{\rho w D}{\mu}\right)^{2}\left(\frac{\gamma^{\prime} D}{\rho w^{2}}\right)=\frac{\rho \gamma^{\prime} D^{3}}{\mu^{2}} \label{3.25} \]
It is convenient, but not necessary, to take these two variables to the one-third power, so that \(w\) and \(D\) appear to the first power; \(w\left(\rho^{2} / \gamma^{\prime} \mu\right)^{1 / 3}\) can be viewed as a dimensionless settling velocity, and \(D\left(\rho \gamma^{\prime} / \mu^{2}\right)^{1 / 3}\) as a dimensionless sphere diameter. Because these two new variables are equivalent to \(C_{D}\) and \(\text{Re}\), the functional relationship for \(C_{D}\) vs. \(\text{Re}\) can just as well be written
\[\left(\frac{\rho^{2}}{\gamma^{\prime} \mu}\right)^{1 / 3} w=f\left(\frac{\rho \gamma^{\prime}}{\mu^{2}}\right)^{1 / 3} D \label{3.26} \]
The usefulness of Equation \ref{3.26} is that the settling velocity appears only on the left side and the sphere diameter appears only on the right side.
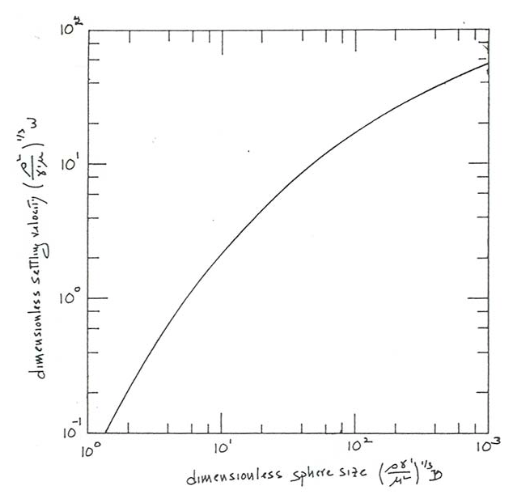
It is now a simple matter to find \(w\) for a given fluid, sphere size, and submerged specific weight by use of Figure \(\PageIndex{3}\), which is a plot of dimensionless setting velocity vs. dimensionless sphere diameter. This curve is obtained directly from that in Figure \(\PageIndex{2}\); you can imagine taking the original data points and forming the new dimensionless variables rather than the old ones to plot the curve in the new coordinate axes of Figure \(\PageIndex{3}\). This emphasizes that these two curves are equivalent because they are based on the same set of experimental data.
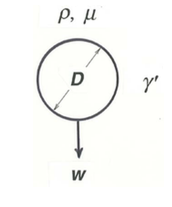
If you are unsatisfied by the roundabout way of arriving at the functional relationship expressed in Equation \ref{3.24}, you might consider making a fresh start on dimensional analysis of the problem of settling of a sphere through a still fluid at terminal velocity (Figure \(\PageIndex{4}\)). Settling velocity \(w\), the dependent variable, must depend on fluid density \(\rho\), fluid viscosity \(\mu\), sphere diameter \(D\), and submerged weight per unit volume \(\gamma^{\prime}\) of the sphere. Each of these must be included for the reasons given in Chapter 2. As before, acceleration of gravity and sphere density do not have to appear separately in the list of variables because they are important only by virtue of their combined effect on \(\gamma^{\prime}\). The five variables \(w\), \(\rho\), \(\mu\), \(D\), and \(\gamma^{\prime}\) should then combine into two dimensionless variables. You can conveniently arrange for one to contain \(w\) but not \(D\) and the other to contain \(D\) but not \(w\) by using the other three variables as the “repeating” variables. You might verify for yourself that this procedure leads to the two dimensionless variables in Equation \ref{3.26}.
Settling at Low Reynolds Numbers
Remember from Chapter 3 that if the Reynolds number based on sphere diameter and relative flow velocity is less than about one, the drag force on the sphere is given exactly by Stokes’ Law, \(F_{D}=3 \pi \mu U D\). This holds in particular for spheres settling under their own weight. Using Stokes’ Law it is easy to develop a useful formula for the settling velocity of spheres that is valid in the Stokes range (\(\text{Re} < 1\)). Write an equation that balances the submerged weight of the sphere, \(\left(\pi D^{3} / 6\right) \gamma^{\prime}\), by the drag force, given by Stokes’ Law, 3\(\pi D \mu w\), where I have used the settling velocity \(w\) as the relative velocity of the fluid and the sphere. Solving for \(w\),
\[w=\frac{1}{18} \frac{\gamma^{\prime} D^{2}}{\mu} \label{3.27} \]
This equation is widely cited and widely used in books and papers on settling of spheres and other bodies, like sediment particles, that have the approximate shape of a sphere, but keep firmly in mind that it applies only in the Stokes range of settling Reynolds numbers \(\rho w D / \mu\).
The Effect of Turbulence on Particle Settling
One clear effect of turbulence on particle setting is the possibility of dispersion. Think about arranging an experiment in which a batch or continuing supply of sediment particles is introduced at the free surface of a channel flow. If the flow is laminar, the particles (if they are identical in size, shape, and density) are identical also in their settling behavior as well, and they all land on the bottom boundary of the flow at the same point,. If the flow is turbulent, however, the settling particles land on the bottom over a wide streamwise range of points, the obvious reason being that each particles traverses (or, perhaps more accurately, finds itself within the domain of) a different set of eddies during its descent, and so it experiences a different set of local fluid velocities. Both the vertical and the horizontal components of fluid velocities within eddies act to spread out, or disperse, the particle trajectories around the overall average trajectory.
It might seem intuitively reasonable to you to assume that the average settling time of the particles in the turbulent flow is the same as the single, well- defined settling time in the laminar flow, because the particles in the turbulent flow are, when viewed on the scale of the particles themselves, just settling through surrounding fluid that is the same as in the laminar case, and the “ups” should balance out the “downs”, on average. That cannot be quite true, however, if only for the reason that the drag coefficient of a sphere moving through a fluid is non-negligibly affected by accelerations and decelerations of the fluid that is moving relative to the particle, and that is exactly what is happening when the particle is in a turbulent flow field.
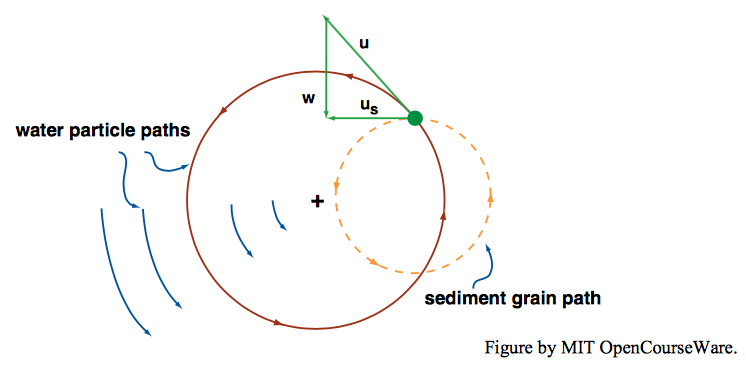
But there is another effect, and one that cannot be ignored, that almost certainly lies outside of your intuition: under certain conditions, a settling particle that finds itself within a rotating eddy tends to become trapped within that eddy! This effect has been studied by Tooby et al. (1977) and Nielsen (1984). In an ideal vortex, rotating about a horizontal axis, a particle within the rising limb describes a circular orbit, which ideally would be closed and would not exhibit any net downward motion (Figure \(\PageIndex{5}\)). In Figure \(\PageIndex{5}\), the tangential velocity of the fluid, u, is proportional to the distance from the center of the vortex.
Simple vector addition of \(u\) and \(w\), the settling velocity of the particle, products a circular trajectory of the sediment particle, with no net settling. In the experiment by Tooby et al. (1977), particles tended to spiral slowly outwards, so that they would ultimately diffuse out of the vortex, but sufficiently fine sediment would be trapped in vortices and would move with the vortex until it dissipated. The mechanism is not very sensitive to the size of the trapped particles, and it should tend to produce less vertical segregation by size than the classical diffusional theory predicts.
References Cited
Lin, C.C., 1955, The Theory of Hydrodynamic Instability: Cambridge, U.K., Cambridge University Press, 155 p.
Nielsen, P., 1984, On the motion of suspended sand particles: Journal of Geophysical Research, v. 89, p. 616-626.
Reynolds, O., 1883, An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and the law of resistance in parallel channels: Royal Society [London], Philosophical Transactions, v. 174, p. 935-982.
Schubauer, G.B., and Skramstad, H.K., 1947, Laminar boundary-layer oscillations and stability of laminar flow: Journal of Aeronautical Science, 14 (2), p. 69-78.
Stokes, G.G., 1851, On the effect of the internal friction of fluids on the motion of pendulums: Cambridge Philosophical Society, Transactions, v. 9, no. 8, p. 287.
Tooby, P.F., Wick, G.L., and Isaacs, J.D., 1977, The motion of a small sphere in a rotating velocity field: a possible mechanism for suspending particles in turbulence: Journal of Geophysical Research, v. 82, p. 2096-2100.
Tritton, D.J., 1988, Physical Fluid Dynamics, 2nd Edition: Oxford, U.K., Oxford University Press, 519 p.


